
Тема 1.2. Анализ устойчивости решения
Рассматривается задача P в канонической форме с m уравнениями (ограничениями), n переменными, m ≤ n:
f0(x) = c0 · x → max при A0x = b0, x ≥ 0.
Строки матрицы A0 линейно независимы,
 – базисное
оптимальное решение,
– базисное
оптимальное решение,
 – оптимальный
базис,
– оптимальный
базис,
 – базисная
матрица.
– базисная
матрица.
 – двойственные
оценки ограничений задачи.
– двойственные
оценки ограничений задачи.
Рассматриваются случаи:
Изменение правых частей ограничений;
Изменение коэффициентов целевой функции;
Изменение набора технологических способов.
1. Изменение правых частей ограничений.
Заменим
вектор b0
в задаче P
на вектор
 .
Получаем задачу Q(b).
.
Получаем задачу Q(b).
Решение устойчиво, когда базис решения не меняется
двойственные оценки остаются постоянными
вектор
 остается решением задачи Q*(b).
остается решением задачи Q*(b).
Определение:
Множество всех векторов b
таких, что задача Q(b)
разрешима и
 ,
назовем областью постоянства двойственных
оценок (ОПДО) задачи Q(b).
,
назовем областью постоянства двойственных
оценок (ОПДО) задачи Q(b).
Графически для двойственной задачи – решение остается постоянным при изменении вектора b, когда изменяется градиент целевой функции двойственной задачи (происходит поворот целевой функции вокруг оптимальной точки).
Оптимальная точка может иметь несколько альтернативных базисов.
Определение:
Множество
 – это множество всех базисов β
матрицы A0
таких, что
– это множество всех базисов β
матрицы A0
таких, что
 (здесь
(здесь
 – базисная матрица для базиса β).
Для
– базисная матрица для базиса β).
Для
 положим
положим
 .
Векторы
.
Векторы
 соответствуют тем задачам Q(b),
в которых базис β
допустим.
соответствуют тем задачам Q(b),
в которых базис β
допустим.
Утверждение:
 .
.
Следствие
1:
 .
.
Следствие
2:
Пусть
 .
Тогда
.
Тогда
 .
.
Определение:
Для любого базиса β
матрицы A0
и произвольного вектора
определим
 как вектор
как вектор
 такой, что
такой, что
 и
и
 .
Вектор
есть базисное решение системы уравнений
.
Вектор
есть базисное решение системы уравнений
 ,
порожденное базисом β.
,
порожденное базисом β.
Следствие
3:
Если
и
,
то вектор
 является решением задачи Q(b).
При
является решением задачи Q(b).
При
 вектор
вектор
 ,
где
,
где
 и
и
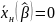 ,
является решением задачи Q(b).
,
является решением задачи Q(b).
Обычно
описание ОПДО ограничивается описанием
 для оптимального базиса
задачи P.
для оптимального базиса
задачи P.
Теорема:
Если
– невырожденное решение задачи P
и в этой задаче нет альтернативного
решения, то
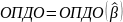 .
.
Доказательство:
Пусть
– невырожденное и единственное решение
задачи P.
Предположим, что
 .
Тогда существует
.
Тогда существует
 .
.
Приведем задачи P и Q(b) к базису .
Так
как
 ,
то базис
недопустим в задаче Q(b).
Следовательно, среди элементов вектора
,
то базис
недопустим в задаче Q(b).
Следовательно, среди элементов вектора
 есть хотя бы один неотрицательный.
есть хотя бы один неотрицательный.
В обоих задачах элементы γj в z-строке вычисляются через элементы матрицы A0, вектора c0 и вектора , значение которого не зависит от правых частей ограничений, поэтому они равны для обоих задач P и Q(b) и все неотрицательны, так как базис оптимален в задаче P.
Зафиксируем
r,
для которого
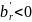 .
Уравнение с этим номером
.
Уравнение с этим номером

Задача
Q*(b)
имеет решение
,
тогда задача Q(b)
разрешима, ее решение неотрицательно.
Тогда, поскольку x
≥ 0,
а правая часть уравнения
,
то существует
 такой, что
такой, что
 (иначе левая часть будет неотрицательна).
(иначе левая часть будет неотрицательна).
Далее
хотим выполнить жорданово исключение
с этим разрешающим элементом
.
Нужно выбрать номер s
так, чтобы элементы преобразованной
z-строки
были неотрицательны
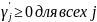 .
Тогда
.
Тогда

Если
 ,
то неравенство выполнено. Пусть
,
то неравенство выполнено. Пусть
 ,
тогда, разделив неравенство, получим
,
тогда, разделив неравенство, получим

Следовательно,
чтобы неравенство выполнялось для всех
j,
для которых
,
нужен максимум отношения 
Так
как
 ,
то
– оптимум в задаче, а значение ЦФ в
задачах Q*(b)
и Q(b)
равно
,
то
– оптимум в задаче, а значение ЦФ в
задачах Q*(b)
и Q(b)
равно
 .
.
Выбрав
этот элемент и проведя жорданово
исключение, приведем задачу к новому
базису
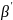 .
.
Пусть
 .
.
Из
неотрицательности
 следует допустимость вектора
следует допустимость вектора
 в Q*(b).
в Q*(b).
После преобразования задачи к новому базису получим значение ЦФ в новой точке:
 ,
,
где вектор – оптимален, а вектор – допустим в задаче Q*(b).
Строгое неравенство невозможно, поэтому
 .
.
Так
как вычитаемое неотрицательно, оно
равно нулю только при
 (так как
и
по выбору). Но отсюда у P
есть альтернативное решение, что
противоречит предположению единственности.
(так как
и
по выбору). Но отсюда у P
есть альтернативное решение, что
противоречит предположению единственности.
Тогда
 .
.
Данный метод называется двойственным симплекс-методом.
Теорема
(общее описание ОПДО):
 .
.
Свойства векторов ОПДО:
Если , то есть вектор двойственных оценок для задачи Q(b);
Если , то
 ,
где
,
где
 ;
;Если , то вектор
 оптимален в задаче Q(b).
оптимален в задаче Q(b).
Прогноз максимального значения ЦФ
Как повлияет изменение правых частей ограничений на значение целевой функции.
Пусть
 ,
.
Нужно проверить неравенства
,
.
Нужно проверить неравенства
 (*)
(*)
Если
они выполняются, то
 и максимум ЦФ изменится на
и максимум ЦФ изменится на
 .
.
Обратная
задача: при каких значениях вектора
 оптимальное значение ЦФ в задаче Q(b)
не меньше, чем заданное число f0:
оптимальное значение ЦФ в задаче Q(b)
не меньше, чем заданное число f0:

Корректировка оптимального решения
Пусть
решение
уже найдено и планируется или ожидается
изменение вектора
 на вектор
.
на вектор
.
Если , то оптимум – и .
Частный случай: вариация правой части одного ограничения
Пусть изменяется правая часть только одного ограничения (с номером k):
и
 .
.
Найдем интересующие нас значения в .
Условие (*) в развернутой форме имеет вид

Подставив
значения
 ,
получим систему линейных неравенств
относительно одной переменной δ:
,
получим систему линейных неравенств
относительно одной переменной δ:

Множество
решений этой совместной системы обозначим
Dk.
Тогда искомый диапазон изменения bk
– это
 .
.
Вектор
 по построению. Поэтому
по построению. Поэтому
 ,
а решение задачи Q(b)
определяется соотношением
,
а решение задачи Q(b)
определяется соотношением
 для
для
 и
и
 для
для
 .
.
Целесообразные изменения правых частей ограничений
Отношение
 называется нормой замены ингредиента
l
ингредиентом k.
называется нормой замены ингредиента
l
ингредиентом k.
Изменение правых частей происходит в ОПДО.
Рассматриваем систему с производством не менее bk ≥ 0 продукта k, потреблением не более bl ≥ 0 ресурса l.
Ограничения

Пусть
 и
и
 – двойственные оценки ограничений, не
равные нулю.
– двойственные оценки ограничений, не
равные нулю.
Увеличение
обязательств по производству на δk
= δ
ведет к ущербу
 .
.
Увеличение
количества имеющихся ресурсов на
 ведет к выгоде
ведет к выгоде
 .
.
На какие дополнительные обязательства можно согласиться, если ущерб покрывается выгодой?
Каковы пределы замены, чтобы оставаться в ОПДО?
Пусть
 и
и
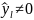 .
.
Вектор
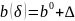 ;
;
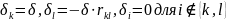 .
.
Система (*) запишется так:
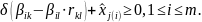
Множество
всех решений
 – это диапазон
– это диапазон
 ,
для которых справедливы рассуждения о
целесообразности замены.
,
для которых справедливы рассуждения о
целесообразности замены.
Очевидно,
что
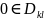 ,
поэтому в
,
поэтому в
 могут содержаться и отрицательные
значения для
– ситуация «обратная» замена.
могут содержаться и отрицательные
значения для
– ситуация «обратная» замена.
