1.3. Напряжения в наклонной площадке

Докажем, что если заданы напряжения в трех взаимно пер­пендикулярных площадках, проходящих через данную точку, то ее напряженное состояние вполне определено. Проведем пло­скость наклонно к осям координат (рис. 2). В результате получим фигуру тетраэдра Оаbс, сливающегося с точкой О при бес­конечном убывании величины его граней. Пусть N – нормаль к наклонной грани тетраэдра. Положение ее определится направ­ляющими косинусами

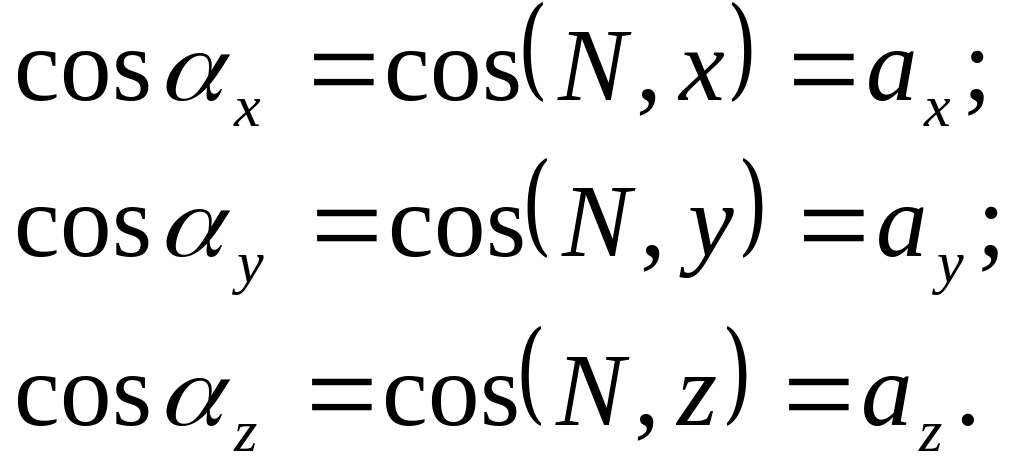
Пусть площадь наклонной грани будет ΔF а площади осталь­ных граней, т.е. треугольников ОВС, ОАС и ОАВ, соответственно ΔF_X, ΔF_у и ΔF_Z. Считаем, что на наклонную грань действует какое-то напряжение S (полное). Напряжения по координатным площадкам также даны. Проекции напряжения S на направления осей координат, или, что то же, компоненты напряжения S по осям координат, обозначаем S_X, S_у и S_Z.

Рисунок 2.

Тетраэдр должен находиться в равновесии. Пишем условия равновесия, проецируя все действующие по его граням силы на оси координат:

Но

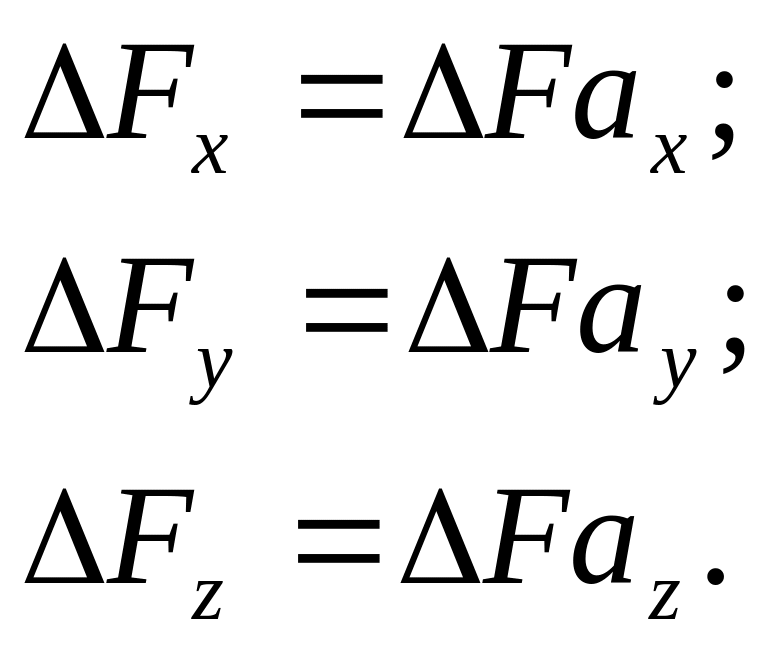
Поэтому

(3)

Суммируя компоненты напряжения S по правилу параллелепипеда, легко получить и само полное напряжение S:

. (4)

Нормальное напряжение в наклонной площадке σ_н опреде­лится как сумма проекций компонент S_х, S_y, S_z на нормаль к площадке:

, (5)

а подставляя значения из уравнения (3), получим

. (5а)

Полное касательное напряжение в наклонной площадке τ найдем по правилу параллелограмма:

. (6)

По полученным формулам можно определить напряжение в любой наклонной площадке. Таким образом, если даны шесть напряжений, действующих в точке по трем взаимно перпенди­кулярным площадкам, то ее напряженное состояние вполне определено.

1.4. Главные нормальные напряжения

Исследуем выражение (5а) для σ_н.

. (5а)

Отложим от начала координат по направлению нормали N (рис. 2) к ка­кой-нибудь наклонной площадке некоторый вектор r, величина которого определяется выражением

,

т.е. примем

,

где А – некоторая произвольная постоянная, определяющая масштаб.

Координаты конца вектора запишутся

,

а следовательно,

.

Подставляя эти значения а в уравнение (5а) и сокращая на r, получим

. (7)

Из аналитической геометрии известно, что полученное урав­нение представляет собой поверхность второго порядка, отнесен­ную центру (отсутствуют х, у, z в первой степени).

С изменением положения наклонной площадки изменятся на­правление и координаты х, у, z конца вектора r, но конец его всегда будет лежать на поверхности, определяемой уравне­нием (7). Отсюда следует, что эта поверхность полностью определяется напряженным состоянием точки. Она носит название поверхности напряжений Коши.

При изменении положения координатных осей, т.е. при отнесении указанной поверхности к другим координатным осям, сама поверхность останется неизменной, а изменятся лишь коэффи­циенты уравнения, т.е. величины напряжений в координатных площадках, поскольку эти площадки станут другими.

Из аналитической геометрии известно, что если поверхность второго порядка отнести не только к центру, но и к сопряженным диаметрам, т. е. к осям, то коэффициенты при произведениях координат обратятся в нуль. Так же можно поступить и с поверх­ностью, определяемой уравнением (7). А это значит, что через точку, находящуюся в напряженном состоянии, всегда можно провести такие три взаимно перпендикулярные плоскости, в кото­рых касательных напряжений не будет и останутся только три нормальных напряжения. Эти три напряжения называют главными нормальными напряжениями, их направ­ления – главными и плоскости, на которых они действуют, – главными плоскостями. Таким образом, если оси координат выбраны параллельно главным направлениям (главные оси), то в соответствующих координатных плоскостях (главных) дей­ствуют только нормальные напряжения – главные.

Отсюда следует, что напряженное состояние точки вполне определяется, если даны направления трех главных осей и вели­чины трех главных нормальных напряжений, которые обозна­чим индексами 1, 2, 3 вместо индексов х, у, z: σ₁, σ₂, σ₃.

Такими же индексами 1, 2, 3 будем в дальнейшем отмечать и главные оси, а также направляющие косинусы площадок, наклонных к этим осям, и соответствующие углы α.

Если напряженное состояние точки задано главными напря­жениями, то напряжения в наклонных площадках выразятся на основании формул (3), (4), (5) и (6) весьма просто. Компоненты по осям координат

. (8)

Полное напряжение

. (9)

Нормальное напряжение

. (10)

Касательное напряжение

. (11)