Требования к содержанию и оформлению отчёта
Отчёт выполняется машинописным способом на листах формата А4, текст располагается с одной стороны. Титульный лист стандартной формы, с указанием темы работы, номера варианта, ФИО и номера группы студента, ФИО и должности преподавателя. Листы отчёта помещаются в скоросшиватель. Допускается скреплять листы степлером и помещать в полиэтиленовый файл.
Отчёт должен включать в себя следующие разделы:
номер варианта и соответствующее ему условие задачи;
экранный снимок (скриншот) окна MS Excel с введёнными данными и полученными результатами (например так, как показано на рисунке 1);
искомые оптимальные значения параметров целевой функции.
Контрольные вопросы
В чём заключается необходимость разработки математических аппаратов для принятия решений?
Что означает термин «линейное программирование»?
Какой смысл вкладывается понятие «целевая функция»?
Какой вид имеет задача линейного программирования в общей и канонической формах?
Каковы наиболее распространённые задачи линейного программирования?
Какая функция табличного процессора MS Excel используется для поиска оптимальных значений параметров целевой функции?
Лабораторная работа №2
Определение оптимальных значений параметров двухмерной целевой функции геометрическим способом Цель работы
Освоить методику определения оптимальных значений параметров двухмерной целевой функции геометрическим способом.
Краткие теоретические сведения
Двухмерная линейная целевая функция является одной из простых вариантов функциональной зависимости. Её графиком является плоскость в трёхмерном пространстве.
Геометрический способ определения оптимальных значений параметров двухмерной целевой функции не требует сложных вычислений и может быть реализован даже без использования компьютера и тем более без специальных возможностей электронных таблиц.
Суть метода заключается в следующем.
Сначала определяются допустимые области значений параметров целевой функции в соответствии с заданными по условиям задачи ограничениями.
Далее определяется экстремальное (минимальное или максимальное) значение целевой функции, при значениях параметров, взятых из допустимой области значений. Для этого, в случае линейной целевой функции, достаточно вычислить её значения на вершинах допустимых областей значений параметров и выбрать нужное (минимальное или максимальное). Геометрический метод может быть использован также и в том случае, если целевая функция не линейна. В этой ситуации необходимо построить график функции, который представляет собой поверхность в трёхмерном пространстве. Для точного построения графика и анализа функции целесообразно воспользоваться возможностями какого-либо программного математического пакета. Наивысшая или низшая точка поверхности (в зависимости от условия задачи) соответствует искомому значению целевой функции.
Значения параметров, соответствующие выбранному значению целевой функции и есть искомое решение оптимизационной задачи.
Методические указания
Рассмотрим применение геометрического способа определения оптимальных параметров линейной целевой функции на примере.
Пусть целевая функция имеет следующий вид:
(1)
На значения
параметров
и
накладываются
следующие ограничения:
(2)
(3)
(4)
(5)
(6)
Решение задачи.
Из неравенств
(2)–(6) видно, что ограничения носят
линейный характер. Их геометрическая
интерпретация следующая. Каждое
неравенство задаёт прямую, которая
делит двумерное пространство (плоскость)
значений параметров
и
на две области.
Одна из них – область допустимых значений
(ОДЗ), значения из другой области не
удовлетворяют неравенству. Любое
сочетание значений
и
является точкой
на плоскости значений параметров
пространства.
Допустимыми
значениями параметров
и
для заданной
целевой функции (1) являются только те,
относительно которых справедливы все
неравенства (2)-(6). На плоскости
это точки, лежащие на пересечении ОДЗ,
задаваемых каждым из неравенств (2)–(6).
Результирующая область, полученная в
результате пересечения ОДЗ, является
областью определения функции (1).
Найдём область определения функции (1). Выразив через получим следующие соотношения:
(7)
(8)
(9)
(10)
(11)
Неравенство (11) означает, что ОДЗ параметров функции (1) лежит в первой четверти плоскости .
Построим графики прямых, задающих ограничения на значения параметров, в координатной плоскости и определим ОДЗ для каждого ограничения.
В соответствии с неравенством (7) ОДЗ находится под соответствующей прямой; с неравенством (8) – под прямой; с неравенством (9) – над прямой; условие (4) – под прямой.
Закрасив пересечение указанных ОДЗ серым цветом, получим график3, приведённый на рисунке 1. Поскольку неравенства (7)-(11) являются нестрогими4, точки отрезков прямых, являющихся границами полученной ОДЗ, также принадлежат этой области.
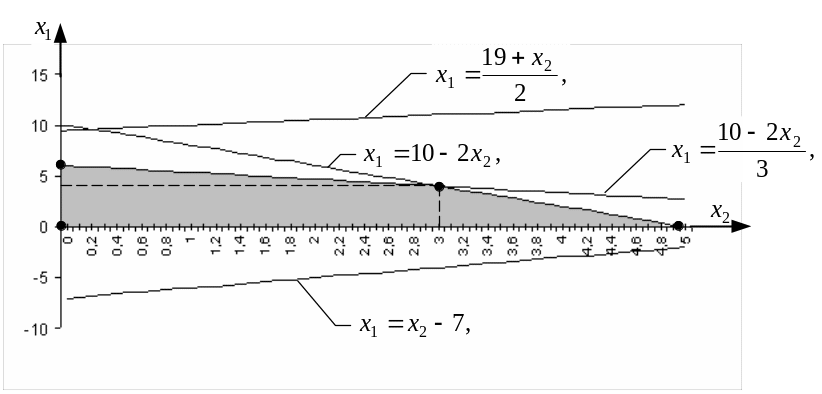
Рисунок 1 – Область допустимых значений параметров целевой функции
Вершины ОДЗ параметров целевой функции отмечены на графике чёрными точками.
Рассчитаем значения целевой функции в отмеченных точках. Полученные значения занесем в таблицу:
-
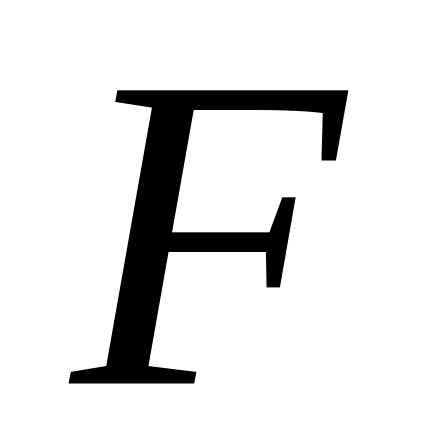
6
0
6
4
3
6,25
0
6
4,5
0
0
0
В приведённой
таблице полужирным начертанием выделена
строка, в которой значение целевой
функции максимально. Таким образом,
значения
,
являются
оптимальными. Задача решена.