Примерный вариан решения индивидуального задания
Найти неопределённые интегралы:
№1.
.
►
=
=
=
=
=
.◄
№2.
.
►
=
=
.◄
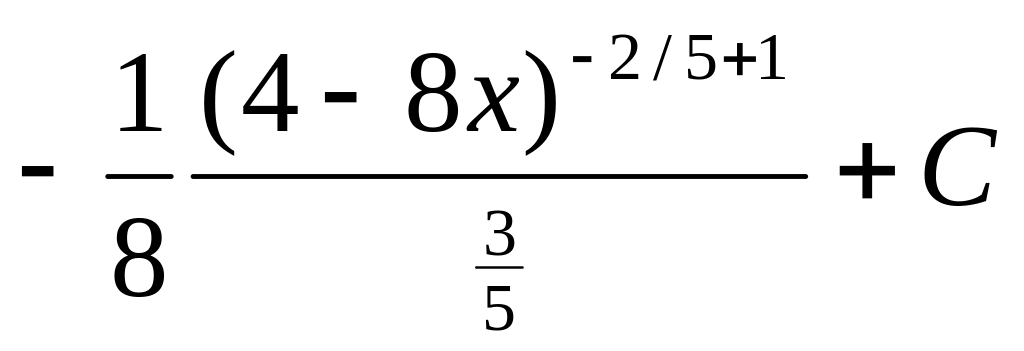№3.
.
►
=
.◄
№4.
.
►
=
.◄
№5.
.
►
=
=
=
=
.◄
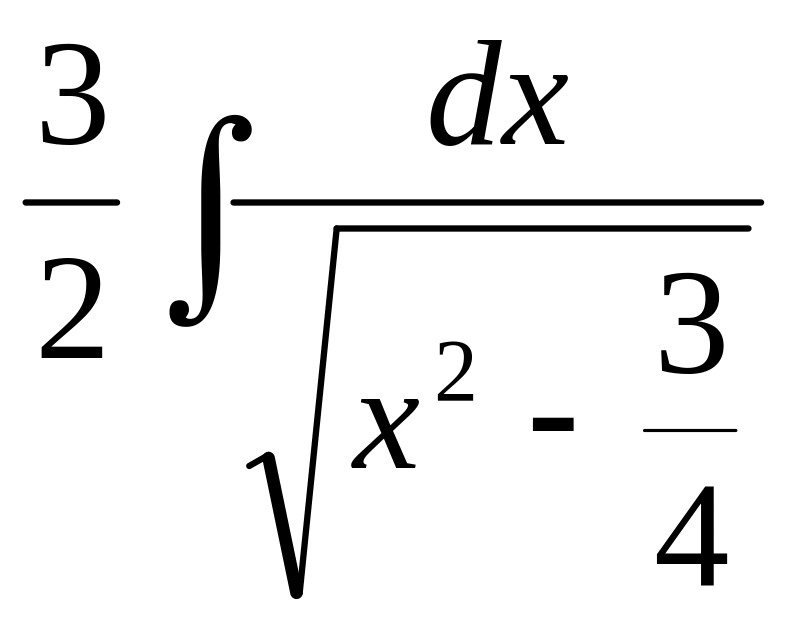№6.
.
►
=
=
=
=
=
.◄
№7.
.
►
=
=
.◄
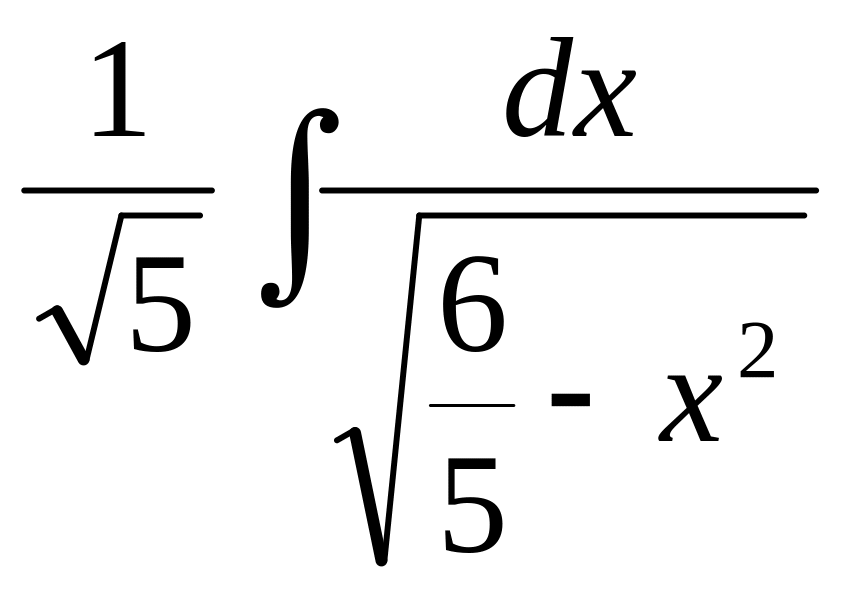№8.
.
►
=
.◄
№9.
.
►
=
=
=
=
=
.◄
№10.
.
►
=
=
=
=
=
.◄
№11.
.
►
=
=
=
=
=
.◄
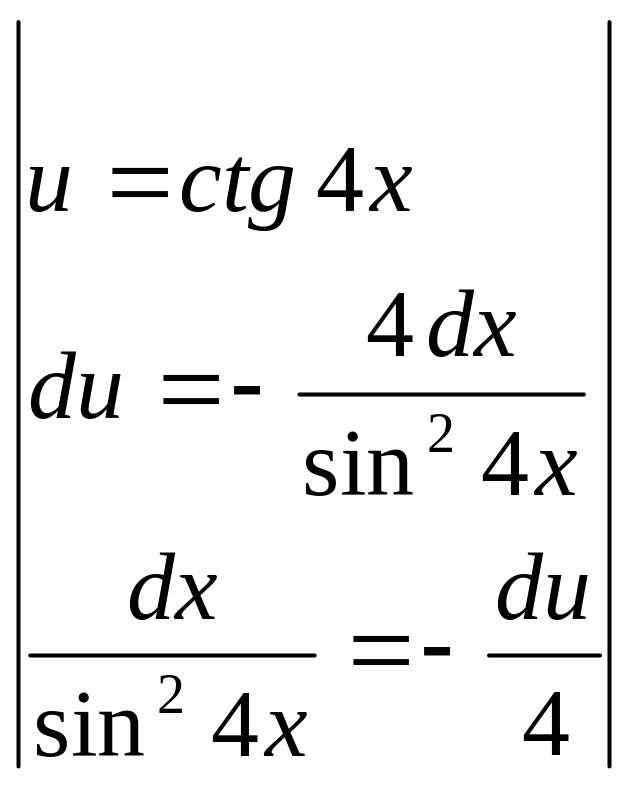№12.
.
►
=
=
=
=
=
=
.◄
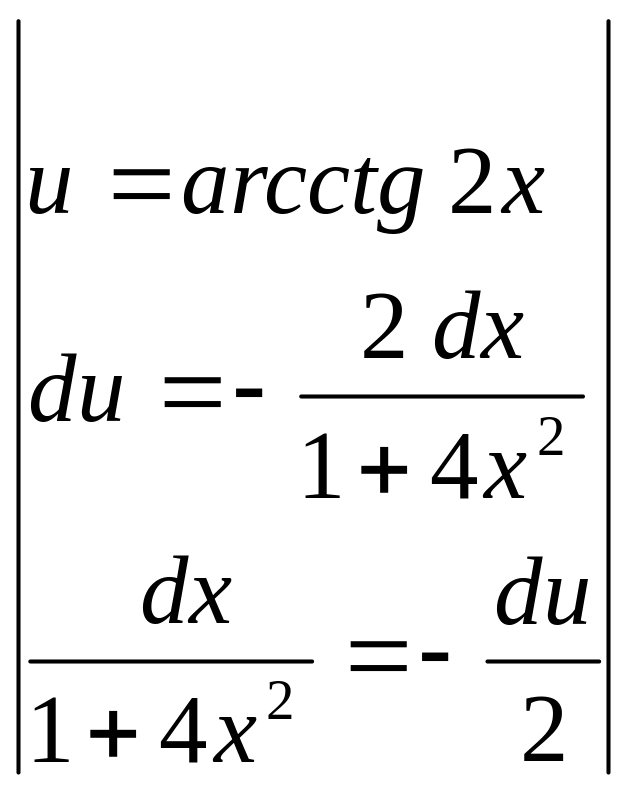№13.
.
►
=
=
=
=
=
.◄
№14.
.
►
=
+
=
=
=
=
=
=
.◄
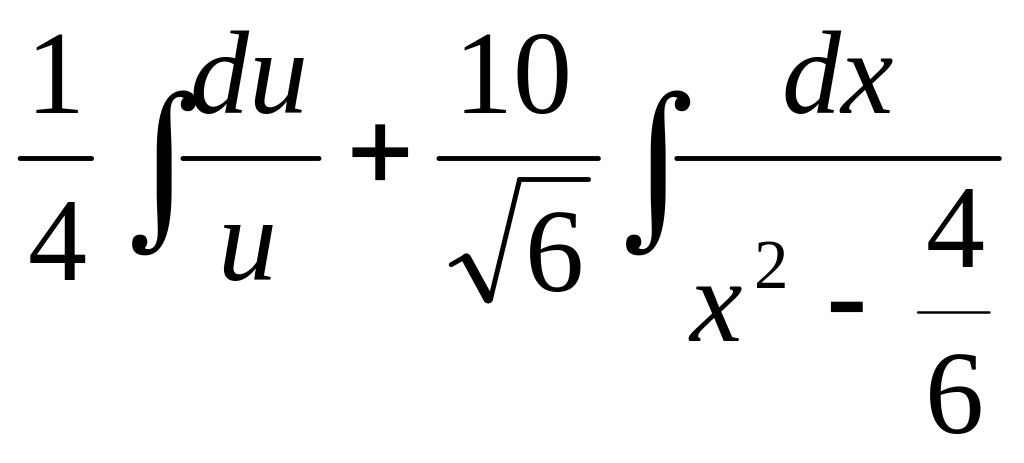№15.
.
►
=
-
=
=
=
=
=
=
.◄
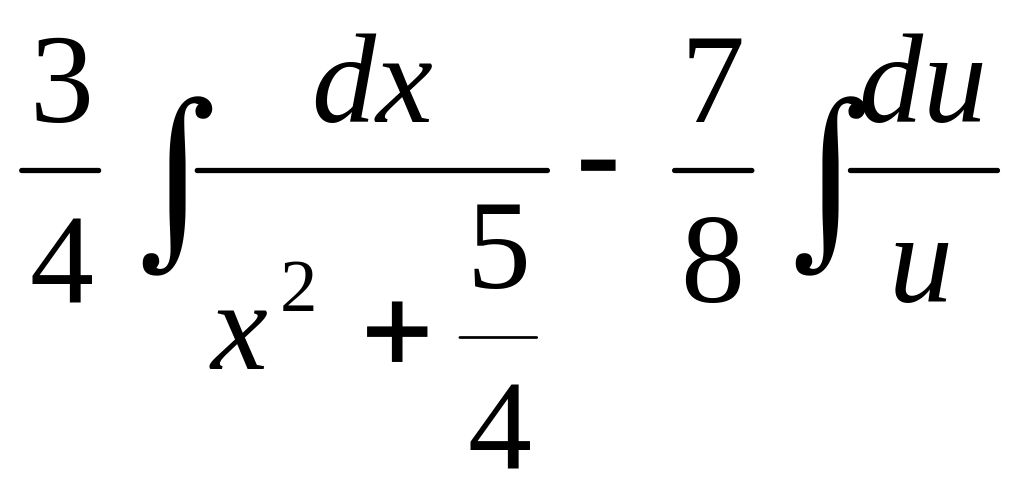№16.
.
►
=
=
=
=
=
.◄
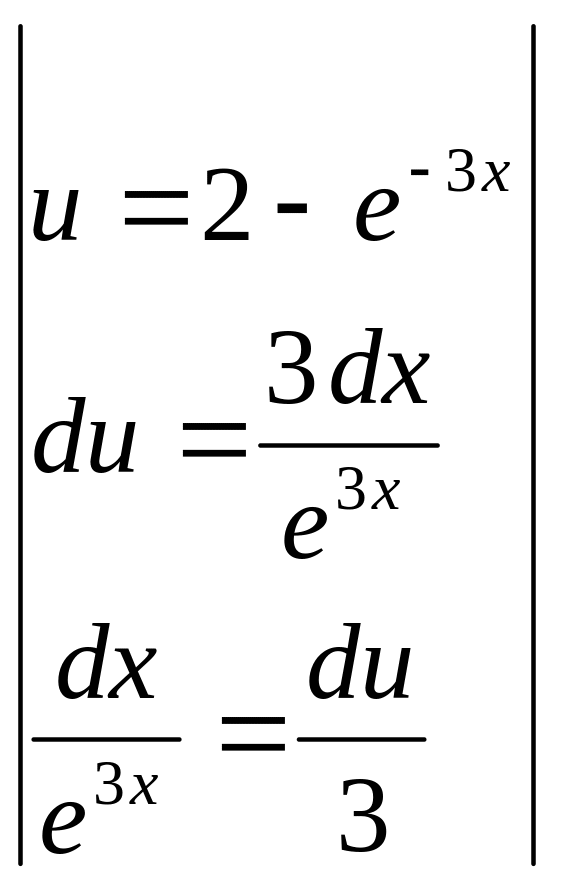Занятие 3 Интегрирование по частям
Цели
Знать:
Суть метода интегрирования по частям;
основные типы интегралов, которые удобно вычислять методом интегрирования по частям;
Уметь:
Применять метод интегрирования по частям при нахождении интегралов.
Пусть u
и v — две функции
аргумента х, имеющие производные
и
.
Тогда справедлива формула:
. (11)
При нахождении интегралов методом интегрирования по частям удобно пользоваться таблицей 1 выбора функции u=u(x).
Таблица 1
Таблица выбора функции u=u(x)
вид интеграла |
u |
|
u=P(x) |
|
u= |
возвратные
|
u=
|
;
;
.
;
;
;
;
.
;
;
.
или u=
.
.
Постановка
задачи. Найти неопределённый интеграл
.
План решения. Пусть v(x) имеет очевидную первообразную V(x), а u(x) — дифференцируемая функция, причём её производная является более простой функцией, чем u(x).
Выбрать u(x), dv, используя таблицу выбора функции u(x);
Найти du; v;
Применить формулу (11).
В некоторых случаях для сведения данного интеграла к одной из формул простейших интегралов формула (11) применяется несколько раз.
Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям (возвратные интегралы);
Записать ответ.
№3. Найти
интегралы: 1)
;
2)
;
3)
;
4)
.
►1)
=
=
=
=
;
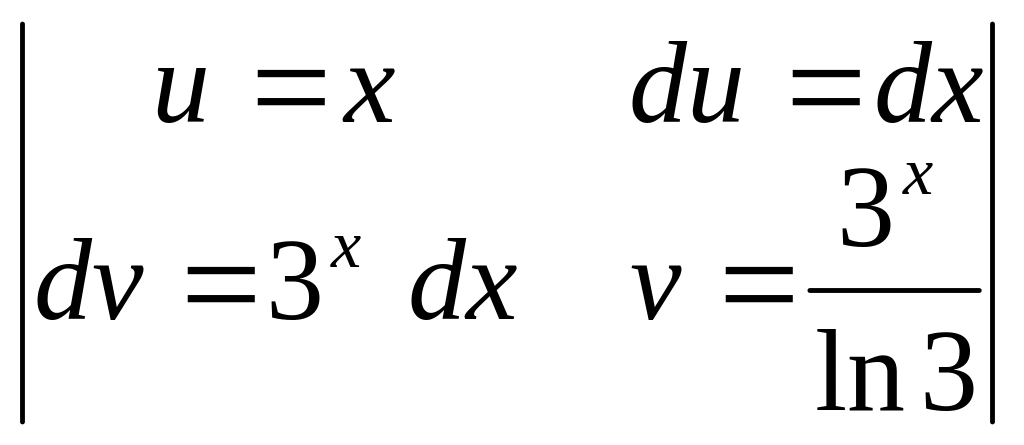2)
=
=
=
=
;
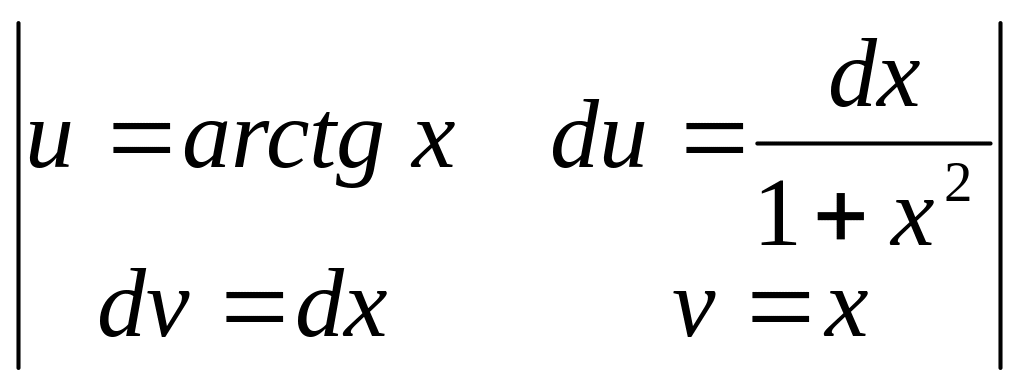3)
=
=
=
.
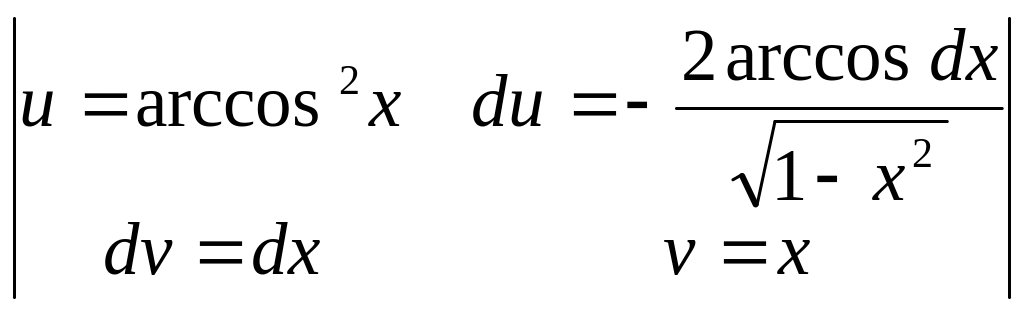Этот интеграл также находим методом интегрирования по частям
=
=
=
=
.
Следовательно,
=
;
4)
=
=
=
.
Этот интеграл также находим методом интегрирования по частям:
=
=
.
Подставив это выражение в последнее равенство, имеем:
по условию
это выражение равно
,
т.е.
=
.
Разрешим данное выражение относительно интеграла (как неизвестного):
,
следовательно,
.◄
Аудиторное занятие
Найти интегралы:
№136.
.
Ответ:
sin x-x
cos x.
№137.
.
Ответ:
.
№138.
.
Ответ:
.
№139.
.
Ответ:
.
№140.
.
Ответ:
.
№141.
.
Ответ:
.
№142.
.
Ответ: xtg
x+ln|cos
x|.
№143.
.
Ответ:
.
№144.
.
Указание. Подстановка t=ln x.
Ответ:
.
№145.
.
Ответ:
.
№146.
.
Ответ:
.
№147.
.
Ответ:
.
Домашнее задание
Найти интегралы:
№148.
.
Ответ: x(ln
x-1).
№149.
.
Ответ:
.
№150.
.
Ответ:
.
№151.
.
Ответ:
.
№152.
.
Ответ: x2
sin x+2x
cos x-2sin
x.
№153.
.
Ответ:
.
№154.
.
Ответ:
.
№155.
.
Ответ:
.
№156.
.
Ответ:
.
№157.
.
Ответ:
.
№158.
.
Ответ:
.
№159.
.
Ответ:
.
Дополнительные задания
Найти интегралы:
№160.
.
Ответ:
.
№161.
.
Ответ: ln
x(ln ln
x-1).
№162.
.
Ответ:
.
№163.
.
Ответ:
.
№164.
.
Указание.
Учесть, что
=
=
=
=
.
Ответ:
.
№165.
.
Ответ:
.
№166.
.
Ответ:
.
№167.
.
Ответ:
.
№168.
.
Ответ:
.
Используя метод интегрирования по частям, доказать, что
№169.
.
№170.
.
Примерный вариант решения
индивидуального домашнего задания
Найти интегралы:
№27.
.
►
=
=
=
=
.◄
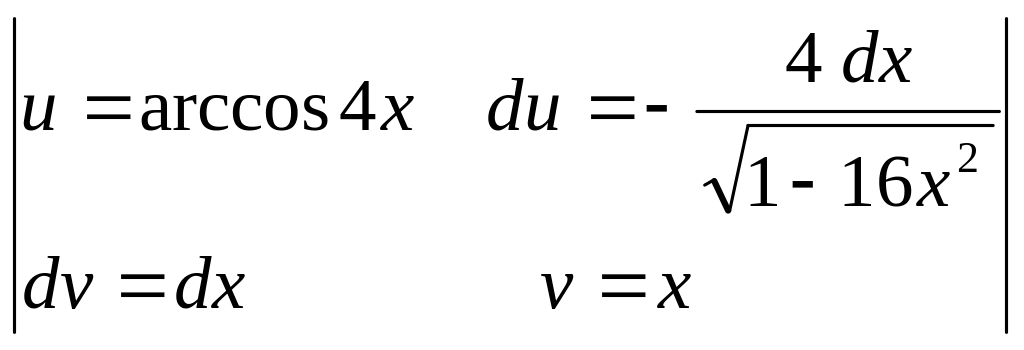№28.
.
►
=
=
=
=
.◄
№29.
.
►
=
=
=
=
=
.◄
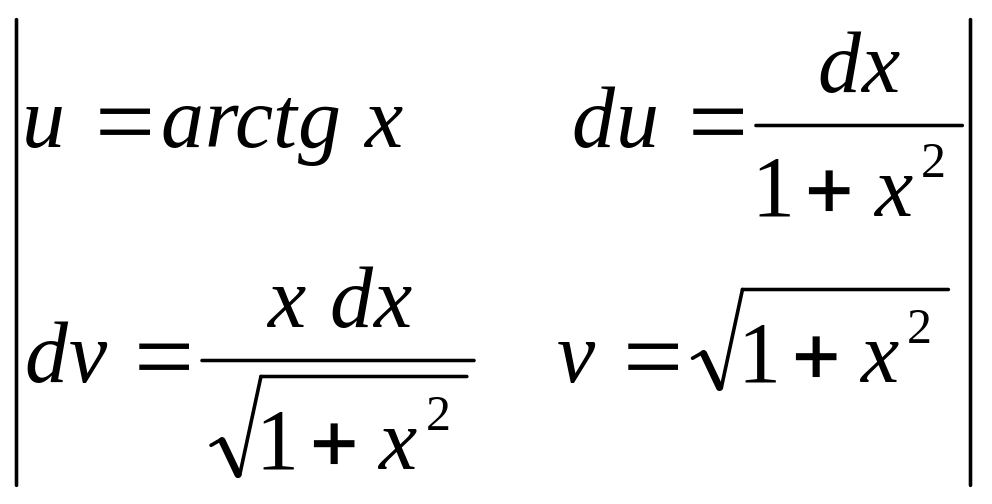№30.
.
►
=
=
=
=
=
=
=
=
=
=
.◄
№31.
.
► =
=
=
=
=
=
.◄
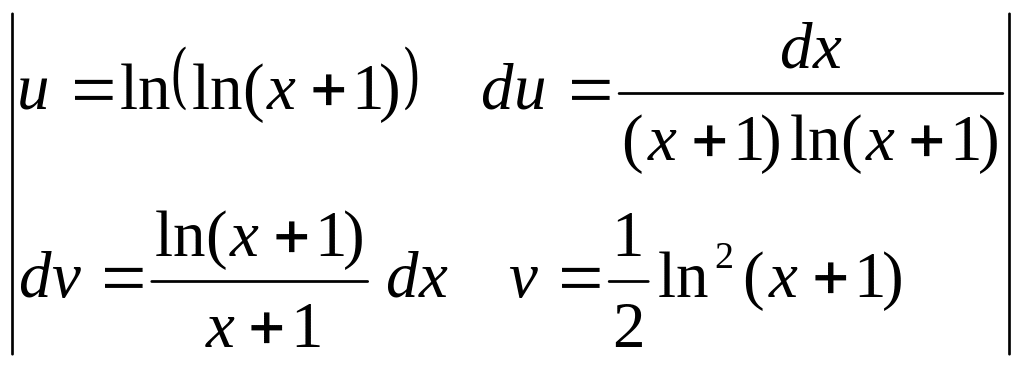Занятие 4
Интегрирование рациональных дробей
Цели
Знать:
Основные теоремы о разложении многочлена на множители;
правила разложения рациональных дробей на простейшие дроби.
Уметь:
Раскладывать многочлен на множители, рациональную дробь на простейшие дроби;
находить неопределённые коэффициенты при разложении дроби на слагаемые методом сравнения коэффициентов и методом частных значений аргумента;
выделять полный квадрат из квадратного трёхчлена;
интегрировать простейшие дроби.
▼Дробно-рациональной
функцией (рациональной дробью)
называется функция, равная отношению
двух многочленов, т.е.
,
где Pm(x)
— многочлен степени m, Qn(x)
— многочлен степени n.
▲
▼Рациональная дробь
называется правильной, если степень
числителя меньше степени знаменателя,
т.е. m<n;
в противном случае (
)
рациональная дробь называется
неправильной.▲
Правильные рациональные дроби
(I)
;
(II)
;
(III)
(знаменатель не имеет действительных корней, т.е. p2-4q<0);
(IV)
(
,
)
(знаменатель не имеет действительных корней),
где A, a, В, С, D, M, N, p, q — действительные числа, называются простейшими дробями.
Постановка
задачи. Найти интеграл
.
План решения.
1. Определить вид дроби;
Если числитель является дифференциалом знаменателя, то воспользоваться способом подведения под дифференциал, т.е.
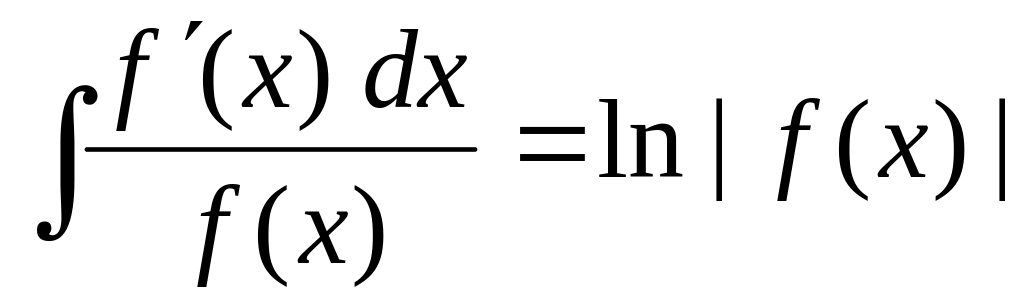;Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби (путём деления числителя на знаменатель);
Если дробь правильная, разложив знаменатель на множители, представить дробь её в виде суммы простейших рациональных дробей (см. таб.2)
Таблица 2
Разложение рациональной дроби в виде простейших дробей
вид множителя |
вид слагаемого |
|
|
|
|
|
|
|
|
Найти коэффициенты в разложении простейших дробей. Для нахождения неопределённых коэффициентов при разложении правильной дроби на слагаемые можно применитьили метод сравнивания коэфициентов или метод частных значений.