2.3.3. Ємність у колі синусоїдної напруги

З курсу фізики відомо, що заряд q та ємність конденсатора C пов'язані співвідношенням:

(2. 29)

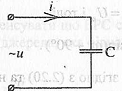
Рис 2.12

Якщо конденсатор підключений до джерела синусоїдної напруги

(2.30)

то в колі буде протікати струм

(2.31)

За аналогією з попереднім розрахунком виконаємо диференціювання синусоїдної напруги і при цьому встановимо фазові співвідношення між напругою і струмом, а також уведемо поняття ємнісного опору.

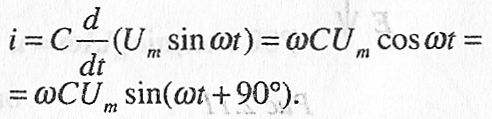(2 32)

Позначимо

(2.33)

і будемо називати його ємнісним опором. Перевіримо розмірність :

Розмірність ємності фарада можна взяти, наприклад, із формули (2.31):

Звідси

З урахуванням (2.33) струм у колі можна записати:

(2.34)

Позначимо , і тоді

(2.35)

Порівнявши напругу згідно з (2.30) і струм згідно з (2.35), можемо зробити висновок: у колі з ідеальною ємністю струм випереджає напругу на 90°. Зсув за фазою між напругою і струмом:

На рис. 2.13 показана векторна діаграма струму і напруги для ємнісного кола.

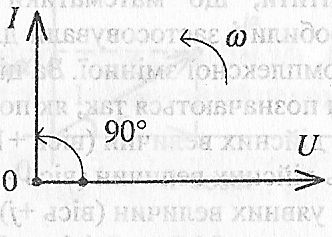
Рис. 2.13

Коло з ідеальною ємністю (R = 0) не споживає із мережі активну потужність. Проте, між джерелом і конденсатором відбувається урівноважене коливання з подвійною частотою активної енергії. Відмітимо, що енергія, яка запасена в конденсаторі, пропорційна квадрату напруги

(2.36)

Розрахунок та аналіз електричних кіл, які містять поєднання R, L, C класичним методом надалі розглядати не будемо. Це краще зробити комплексним методом, який є зручним апаратом для розрахунку електричних кіл змінного струму.

2.4. Загальні відомості про комплексний метод розрахунку кіл змінного струму

Наприкінці XIX століття американський вчений Штейнметц уперше почав застосовувати для розрахунку електричних кіл змінного струму комплексний (символічний) метод. Сутність методу полягає в тому, що замість геометричних дій над векторами проводяться відповідні математичні дії над символами, що однозначно визначають параметри цих векторів.

Дійсно, якщо на площині зображений вектор, то його модуль (довжина) і аргумент (кут відносно будь-якої осі, прийнятий за початок відліку) однозначно визначає параметри цього вектора. Вектор, у свою чергу, є синусоїдним струмом або напругою (див 2.4) або параметри вектора можуть бути однозначно визначені його проекціями на осі прямокутної системи координат.

Потрібно відмітити, що математики задовго до кінця XIX століття розробили і застосовували для своїх досліджень теорію функцій комплексної змінної. За цією теорією осі комплексної площини позначаються так, як показано на рис. 2.14:

• додатна вісь дійсних величин (вісь +1),

• від'ємна вісь дійсних величин (вісь -1),

• додатна вісь уявних величин (вісь +j),

• від'ємна вісь уявних величин (вісь -j).

Нехай вектор А має модуль А (без точки) і аргумент α(альфа) відносно осі +1.

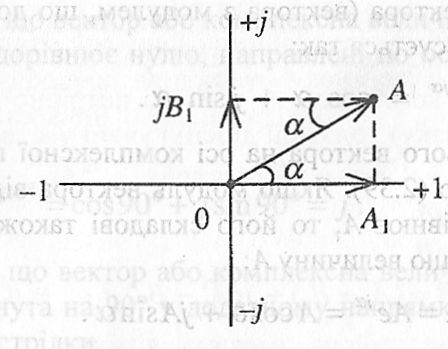
Рис 2.14

Кути прийнято відкладати від осі +1, додатним напрямом відліку прийнято напрям проти годинникової стрілки; за годинниковою стрілкою від осі +1 відкладаються кути зі знаком "мінус".

Зображений на рис 2.14 вектор А може бути записаний у двох формах:

(2.37)

Це так звана показникова форма запису комплексного числа.

Або:

(2.38)

Ця форма запису називається алгебраїчною, тут – проекція шуканого вектора на вісь дійсних величин, а – проекція на вісь уявних величин.

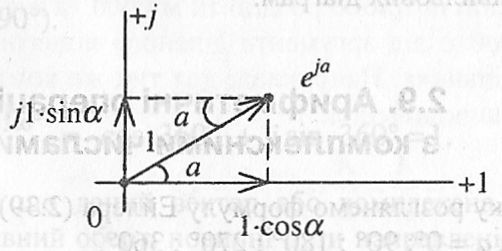
Рис. 2.15

Потрібно відмітити, що в основі подання векторів або будь- яких комплексних чисел лежить формула Ейлера, яка для одиничного вектора (вектора з модулем, що дорівнює 1, див. рис. 2.15) записується так:

(2.39)

Проекції цього вектора на осі комплексної площини показані формулою (2.39). Якщо модуль вектора відрізняється від одиниці і дорівнює А, то його складові також повинні бути помножені на цю величину А:

(2.40)

Останню форму запису називають тригонометричною.

Проекцію на вісь дійсних величин називають дійсною частиною комплексного числа, це А₁ у формулі (2.38) або у формулі (2.40).

Проекцію на вісь уявних величин називають уявною частиною комплексного числа, це B₁ у формулі (2.38) або альфа у формулі (2.40).

Очевидно, для математичного запису вектора не обов'язково на комплексній площині зображати сам вектор. Достатньо математично записати координати точки, яка є кінцем шуканого вектора, вважаючи, що початок вектора знаходиться у нульовій точці комплексної площини. Необхідні математичні дії над комплексами виконуються більш швидко і точно, кін­цевий результат при необхідності може бути поданий не тільки в потрібному аналітичному записі (алгебраїчному, тригонометричному, показниковому), але також за допомогою векторів або хвильових діаграм.