11.3.Полиномиально-разрешимые частные случаи np-полных задач

Сразу же после появления теории NP-полноты большой интерес вызвал вопрос поиска полиномиально разрешимых частных случаев таких задач, но интерес к этому направлению достаточно быстро угас. Оказалось, что тривиальные случаи задач можно решать за полином, а , а большинство «сильных» упрощений, все равно, оставляют задачу в NPC.

Выше мы видели, что 3-КНФ – выполнимость еще лежит в NPC и только 2-КНФ – выполнимость лежит в P.

Для задачи коммивояжера связный граф с максимальной степенью вершин, равной двум, является просто гамильтоновым одним циклом. Задача тривиальна. Но уже для кубического графа получаем NP-трудную задачу. Если мы наложим ограничение в виде условия треугольника или потребуем, чтобы веса ребер принимали только одно из двух фиксированных значений, то снова получаем NP-трудную задачу.

Для задачи ЦЛП известен случай полиномиальной разрешимости – n=const. Но это снова очевидная ситуация.

Задача о клике полиномиально разрешима для следующих графов: степень вершин ограничена константой; планарные графы, реберные графы.(Граф G является реберным графом, если существует граф G’ такой, что вершинам G соответствуют ребра G’ и в G существует ребро (x,y) тогда и только тогда. когда x и y имели в G’ общую концевую вершину.)

Задача гамильтонов цикл лежит в NPC даже если выполняются следующие условия: граф двудольный; максимальная степень вершины равна трем; граф планарен; в графе задан гамильтонов путь. Задача полиномиально разрешима для реберных графов и графов с максимальной степенью вершины, равной двум.

11.4.Методы направленного перебора

Пусть дана Z - задача оптимизации –пара (F,c) , где F –множество решений, а – c функция стоимости, отображающая элементы F на множество действительных чисел. Требуется найти такую x* точку из F, на которой значение функции c(x*) обладает определенным свойством, например, минимально, максимально и пр. Рассмотрим, например, задачу на минимум.

В задаче коммивояжера – это множество всех гамильтоновых циклов графа, в задаче ЦЛП – множество целочисленных точек многогранника и т.п.

Методы направленного перебора основаны на нескольких простых соображениях.

1. Экстремальное значение на множестве и на подмножестве связаны определенными неравенствами. В случае задачи на минимум c_G - минимум функции стоимости на подмножестве G 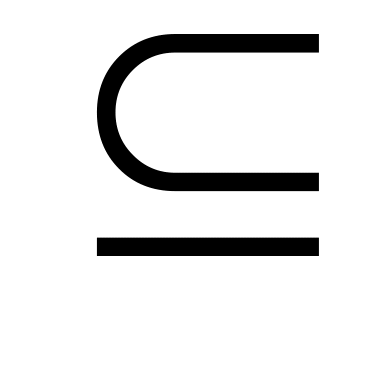F не превосходит c(x*) - минимума функции стоимости на всем множестве.

2. Пусть l(x*)≤ c(x*) ≤ u(x*), т.е. l(x*) и u(x*) - нижняя и верхняя оценка для c(x*). При этом значения l(x*) и u(x*) могут быть найдены полиномиальным алгоритмом.

3. Все множество F может быть иерархически разбито на непересекающиеся подмножества. Это разбиение представимо в виде дерева ветвей. Пример приведен на рисунке.

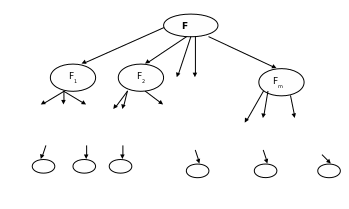
Здесь каждая вершина – некоторое множество допустимых решений. Все множество решений, соответствующее каждому родительскому узлу разбивается на подмножества решений, соответствующих узлам-потомкам. Здесь все подмножества родительского узла не пересекаются, а их объединение в точности дает множество, соответствующее родительскому узлу. Листья дерева – одноэлементные множества.

4. Если для некоторого узла дерева G F выполняется соотношение

l(x*)<c_G,

то это означает, что оптимальное решение x* не может находиться среди допустимых решений, соответствующих данному узлу, а все множество G можно исключить из дальнейшего рассмотрения. (Отрезать ветвь дерева.)

Отсюда следует другое название методов направленного перебора – методы ветвей и границ.

Пример. Задача коммивояжера.

Получение оценок.

Рассмотрим множество подстановок n-элементного множества. Каждой подстановке можно сопоставить множество ребер полного графа: (1,i₁),(2,i₂),…,(n,i_n). Если задана матрица весов ребер, то сумма весов ребер подстановки – это длина (вес) подстановки. Задача нахождения постановки минимального веса называется задачей о назначениях. Она решается, так называемым, венгерским алгоритмом за время O(n³). Гамильтоновым циклам графа соответсвуют одноцикловые подстановки. Задача коммивояжера – это задача поиска одноцикловой подстановки минимальной длины. Одноцикловые подстановки – это подмножество всех подстановок, поэтому длина минимальной подстановки не превосходит длины минимальной одноцикловой подстановки. Таким образом в качестве нижней оценки l(x*) можно взять решение задачи о назначениях – длину минимальной подстановки.

Верхней оценкой u(x*) может быть длина любого допустимого решения, например решения, полученного алгоритмом «иди в ближайшую» («жадный алгоритм»): из вершины 1 идем в вершину i₁ такую, что ребро (1,i₁) имеет минимальный вес среди всех ребер вида (1,j), на втором шаге из вершины i₁ идем в вершину i₂ 1 такую, что ребро (i₁,i₂) имеет минимальный вес среди всех ребер вида (i₁,j), j 1; из вершины i₂ идем в вершину i₃ 1, i₂ такую, что ребро (i₂,i₃) имеет минимальный вес среди всех ребер вида (i₂,j), j 1,i₂. И так далее. На последнем шаге замыкаем цикл.

Правила ветвления.

Здесь F –множество всех гамильтоновых циклов, F₁ -множество гамильтоновых циклов, начинающихся с ребра (1,2) , F₂ - с ребра (1,3),…, - F_n-1 - с ребра (1,n). Аналогично множество F₁ разбивается на подмножеств, а именно тех множеств, В которые входят гамильтоновы циклы, начинающиеся с пары ребер (1,2),(2,3); (1,2),(2,4);…;(1,2),(2,n). Каждому листу дерева соответствует один гамильтонов цикл. Очевидно, что при таком построении все требования выполняются.

Схема прохода дерева.

Начинаем с корня. Вычисляем для корня нижнюю и верхнюю границу c(x*). Далее переходим поочередно к ветвям: F₁ , F₂,…, F_n-1. Так как множество гамильтоновых циклов, соответствующее F₁ , F₂,…, F_n-1 - это подмножество всех гамильтоновых циклов, то нижняя оценка может только увеличиться при переходе от F к каждому из множеств F₁ , F₂,…, F_n-1.Для каждой ветви вычисляем нижнюю оценку. С помощью нее получаем нижнюю оценку длины гамильтонова цикла уже только для гамильтоновых циклов соответствующего подмножества: F₁ , F₂,…, F_n-1. Если для какого-то подмножества эта полученная оценка превосходит u(x*), то ветвь обрезается. Если не превосходит, то происходит ветвление этого множества на подмножества по принципу, описанному выше. Если ветвь не обрезается, то с помощью этого подмножества можно попытаться улучшить верхнюю оценку u(x*). Для этого нужно жадным алгоритмом обойти нефиксированные ребра и полученный результат сложить с суммой весов фиксированных ребер. Если мы получим гамильтонов цикл, вес которого меньше u(x*),то для дальнейшего будем использовать этот гамильтонов цикл, а его длину примем за u(x*).

Вместо (или вместе) задачи о назначениях можно использовать другие задачи из класса P такие, что гамильтоновы циклы будут частными случаями допустимых решений этих задач. Например, в алгоритме Балаша-Кристофидеса (1981 г.) используется четыре задачи (причем параметризованные), на основе решений которых получается оценка для c(x*). При тестировании алгоритма получены были следующие результаты. Решалось 120 задач с размерностями 50, 75,…,325 (по 10 задач каждой размерности. Во всех случаях было получено очное решение, причем время решения задачи не превышало полутора минут.

Согласно таблице из раздела 6.4 полный перебор для n=50 занял бы годы на самой современной машине того времени. Стратегия перебора в методе ветвей и границ содержит эвристические правила. Как при организации ветвления, так и при обрезании ветвей. Для любого набора правил всегда можно подобрать пример такой, что ни одну ветвь нельзя обрезать и придется ветвиться до листьев. (Например, в нашем случае веса всех ребер, кроме двух, одинаковы, а два оставшихся имеют «большой» и «маленький» вес, причем маленькое ребро не захватывается жадным алгоритмом до самого листа.) В этом случае мы получаем полный перебор.

Вообще говоря, проблема тестирования подобных алгоритмов – вопрос сложный и выходящий за пределы нашего курса. Мы лишь просто хотим сказать, что направленный перебор возможен и иногда эффективен. В 1970-е – 1980-е годы было построено большое количество алгоритмов этого типа для таких задач как задача о покрытии, задача ЦЛП, задача о рюкзаке и др. Поэтому, если вам придется на практике решать задачи из NPC, то можно поискать готовый алгоритм и попробовать его применить.