9.3.Теорема Кука
Само понятие NP-полноты - инструмент исключительно описательный. Из приведенных выше утверждений легко получить следующую теорему.
Теорема. Если L1L2 и L1 является NP-полной задачей, тогда Lтакже NP-полная задача.
Это утверждение позволяет гипотетически разбить весь класс NP на части. То есть выделить в нем некоторое множество сравнительно простых задач. Это класс P. И множество задач самых сложных – класс NPC. Это множество NP-полных задач.
Пусть, например, появилась некоторая новая задача Z. Мы пытаемся оценить ее сложность. Если мы придумали полиномиальный алгоритм ее решения, то она относится к классу P. Если наши усилия по построению такого алгоритма долго не увенчиваются успехом, то мы можем попытаться доказать с помощью сформулированной теоремы NP-полноту задачи Z. Если это удается, то можно утверждать, что новая задача в некотором смысле не проще многих известных задач, NP-полнота которых уже доказана.
Но доказательство NP-полноты можно проводить разными способами. Пока нам ясно два: использовать сформулированную только что теорему и технику сведения одной конкретной задачи к другой или непосредственно исходить из определения. Первый способ кажется предпочтительней (да так, наверное, и есть). Но для применения теоремы нужно иметь хотя бы одну NP-полную задачу.
Вот в этом и основной смысл теоремы Кука. Он доказал, пользуясь только определением, NP-полноту одной конкретной задачи. Всюду в дальнейшем пустой символ будем обозначать через .
Теорема Кука. Задача о выполнимости (ЗВ) NP-полна.
Мы приведем схему доказательства этой теоремы, взятую из лекций А.Разборова.
По определению NP-полноты мы должны доказать два факта.
ЗВ лежит в NP.
Любая задача Z из NP полиномиально сводится к ЗВ.
Для доказательства первого факта мы должны построить НМТ, которая за полиномиальное время решает ЗВ. Это очевидно. Действительно, вход задачи - КНФ от p переменных x1,…,xp, заданная в виде конъюнкции из m конъюнкций. Если она обращается в единицу на некотором наборе значений переменных x1=a1,…,xp=ap, то угадывающая головка данный набор длины p напишет. Подстановка в формулу и проверка требует полиномильного по длине входа времени.
Доказательство второго факта строится по следующему принципу. По входу w задачи Z строится вход задачи ЗВ. Это некоторая КНФ w, которая обращается в единицу тогда и только тогда, когда на слове w задача Z имеет ответ "да".
Так как задача Z (язык LZ) лежит в NP, то имеется НМТ TZ={S, A, F, q0, }, решающая эту задачу (допускающая язык LZ) за полиномиальное от длины входа |w|=n время. Пусть p(n) - полином, ограничивающий число тактов работы NMT. Для простоты индексации будем считать, что подобрано подходящее k, такое что p(n)<nk.
Идея состоит в том, чтобы смысл данной фразы записать в виде логической формулы. Наглядно представить себе подобную формулу позволяет подробное описание всех шагов вычисления TZ на входе w. Их легче всего представить в виде таблицы, строки которой - конфигурации работы TZ на стадии проверки. Такая таблица называется допускающей таблицей и имеет вид.
Номера конфигураций/ячеек |
-nk |
... |
v+1 |
v |
... |
-1 |
0 |
1 |
... |
n |
n+1 |
... |
nk |
1 |
|
… |
|
av |
… |
a1 |
q0 |
w1 |
… |
wn |
|
… |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ее размеры очевидным образом ограничены условием полиномиального времени работы: количество столбцов не превосходит времени работы, а число строк просто равно числу тактов работы НМТ. В первой строке написана отгадка a1,…,av и код слова индивидуальной задачи (слово языка LZ) w1,…,wn . В следующей строке приведена конфигурация НМТ после первого такта ее работы и т.д. Ясно, что построение такой таблицы потребует полиномиального по длине входа n времени.
Грубо говоря, эта таблица будет теперь входом задачи о выполнимости. То есть, по ней мы построим некоторую КНФ, которая выполнима тогда и только тогда, когда данный вход описывает именно таблицу допустимости.
Логика же здесь простая. Должны быть справедливы одновременно четыре утверждения.
В каждой клетке таблицы записан ровно один символ, причем это или пустой символ, или буква алфавита A, или символ (номер) состояния из S. (Пусть это условие можно записать в виде некоторой конъюнкции 0).
В первой строке записана начальная конфигурация, например, в том виде, что на рисунке выше. (Пусть это условие можно записать в виде некоторой конъюнкции start).
В последней строке записана некоторая допускающая конфигурация, т.е. машина остановилась в состоянии qy. (Пусть это условие можно записать в виде некоторой конъюнкции accept).
Каждая следующая строка в таблице получается вследствие допустимого перехода МТ. Этот переход осуществляется путем выполнения некоторой команды qiajqrat{Z},заданной функцией переходов .(Пусть это условие можно записать в виде некоторой конъюнкции computs).
В результате получаем КНФ
w = 0&start&accept&computs.
Если она обращается в единицу, то выполняются все вышеприведенные четыре условия, которые влекут за собой допустимость некоторого корректного вычисления НМТ на индивидуальной задаче w некоторой массовой задачи Z. Набор значений переменных в задаче о выполнимости, на котором КНФ обращается в единицу, и даст нам содержимое допускающей таблицы, которая и описывает данное корректное вычисление.
С другой стороны, если мы имеем некоторое корректное вычисление НМТ на индивидуальной задаче w некоторой массовой задачи Z, то оно может быть представлено в виде допускающей таблицы, по которой строится КНФ
w = 0&start&accept&computs.
И просто по построению эта КНФ должна быть выполнима на том входе, который задает содержимое допускающей таблицы.
Остается построить за полиномильное время четыре вышеупомянутые конъюнкции.
В качестве переменных рассмотрим множество булевских переменных
Var = {xij, i=-nk,…,nk; j=-nk,…,nk; SA}.
Эти переменные обращаются в единицу, если на пересечении i-й строки и j-го столбца допускающей таблицы стоит символ .
Покажем, что первая из четырех конъюнкций 0 выражается в следующем виде.
Знак конъюнкции означает, что логическое условие в скобках должно выполняться для каждой клетки таблицы. Первое из условий в круглых скобках соответствует требованию наличия в каждой клетки таблицы хотя бы одного символа (из области значений введенного выше множества переменных Var). То требование, что в клетке должно быть не более одного символа, записано в виде логического выражения во второй круглой скобке формулы для 0.
Так как число состояний и число символов алфавита являются константами, то длина выражения в скобках от n не зависит. Поэтому длина всей конъюнкции 0 равна O(n2k).
Следующая конъюнкция start выражается формулой
Здесь все понятно. Это просто логическая запись требования к содержимому первой строки таблицы. Для индивидуального входа w и отгадки a оно должно быть именно таким, как показано на рисунке выше. Длина всей конъюнкции start равна O(nk).
Что касается конъюнкции accept , то она выражается формулой
Смысл в том, что в последней строке допускающей таблицы должна стоять конфигурация, содержащая символ конечного состояния. Длина всей конъюнкции accept равна O(nk).
Самым сложным является вычисление конъюнкции computs. Мы не будем выписывать его во всей строгости, приведем лишь общую идею формулы. Как уже говорилось выше, эта конъюнкция должна быть формальной записью того условия, что каждая следующая строка в таблице получается вследствие допустимого перехода МТ. А сам переход осуществляется путем выполнения некоторой команды qiajqrat{Z},заданной функцией переходов . Обозначим через i(i+1) условие того, что правильно осуществлен переход между соседними конфигурациями. Тогда computs выглядит следующим образом
Для нахождения i(i+1) заметим следующее. Две соседние строки допускающей таблицы различаются не более чем в трех клетках. То есть все изменения сосредоточены в "окошке" таблицы" следующего вида
-
(i,j-1)
(i,j)
(i,j+1)
(i+1,j-1)
(i+1,j)
(i+1,j+1)
Первая строка таблицы правильно заполнена в силу условия start. Заполняем таблицу, начиная со второй строки. Поэтому в паре i-й и (i+1)-й строк проверка того условия того условия, что каждая следующая строка в таблице получается вследствие допустимого перехода МТ, сводится к правильности проверки заполнения (i+1)-й строки. Для этого "проходим" всю пару вышеупомянутыми окошками.
Если в верхней части окошка нет символа состояния, то в нижней части символы алфавита совпадают с верхними. Как только символ состояния встретился, читаем стоящий рядом символ алфавита. Так как число состояний, число букв алфавита и число правил переходы - постоянные величины, то логическое условие, определяющее правильность перехода между соседними конфигурациями, не зависит от n. Действительно, вспомним теорему о полноте базиса из трех булевых функций: , и . В качестве простого упражнения можно записать упомянутое условие через эти функции.
Но для построения конъюнкции i(i+1) все равно нужно пройти всю строку. Поэтому и длина всей конъюнкции computs равна O(n2k).
Таким образом, все четыре требуемые конъюнкции построены за полиномиальное время.
Теорема доказана.
Итак, у нас появилась первая NP-полная задача. Для доказательства NP-полноты следующей задачи можно либо повторить что-то похожее на только что доказанную теорему, либо использовать понятие сводимости.
Рассмотрим несколько примеров.
Выше мы рассмотрели пример.
Пример. "Задача выполнимости" "Задача 3-выполнимости".
На основе теоремы Кука из него следует существование еще одной NP-полной задачи.
Пример. "Задача 3-выполнимости" "ЦЛП".
Задача "ЦЛП" (целочисленного линейного программирования) :
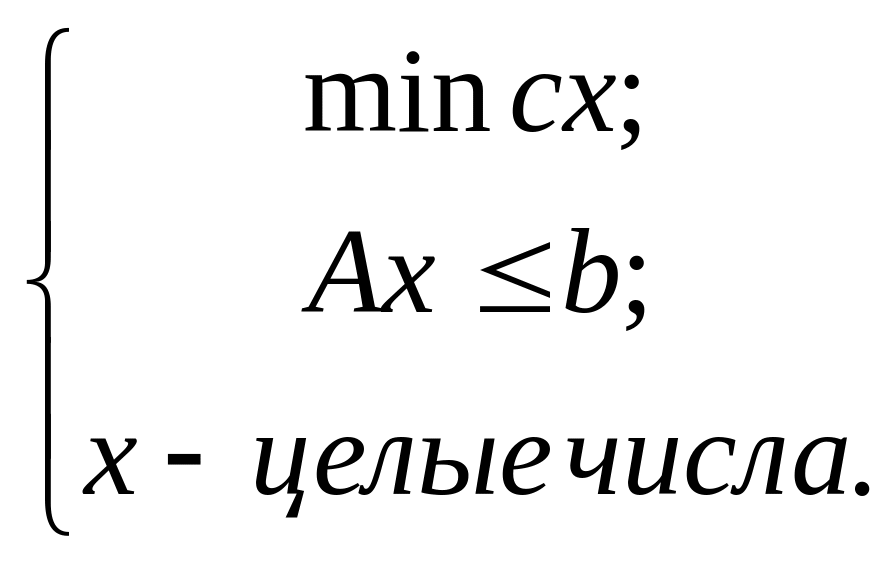
Из того, что "Задача 3-выполнимости" является NP-полной следует, что она, являясь частным случаем ЗВ, все же "не проще" последней. Не проще именно сточки зрения теории NP-полноты. Известные же переборные алгоритмы могут быть в чем-то более изощренными для этого частного случая и иметь "в константу" или "или в полином" раз меньшую трудоемкость.
Из приведенного примера следует, что "Задача k-выполнимости" является NP-полной для любого k>2. А как быть со случаем k=2 ?
Теорема. "Задача 2-выполнимости" полиномиально разрешима.
Схема доказательства.
В "Задаче 2-выполнимости" в каждой дизъюнкции не более двух литералов. Пусть B такая КНФ от переменных x1,…,xn. Сопоставим B ориентированный граф G=(V,E), множество из 2n вершин которого помечено переменными x1,…,xn или их отрицаниями. Вершины с пометками a и b соединены в графе ребром ab, если в B имеется дизъюнкция вида ab.
Строго связной компонентой графа называется множество вершин графа, между любой парой которых существует цепь (ориентированный путь) в этом графе. Если, например, граф c n вершинами и m ребрами задан списками вершин, то за O(nm) легко найти все его строго связные компоненты. Покажем теперь, что нахождение этих компонент почти эквивалентно решению задачи 2-выполнимости. Для этого докажем, что формула В выполнима тогда или только тогда, когда в G не существует строго связной компоненты, в которую входят вершины помеченные переменной и ее отрицанием.
Пусть B выполняется на наборе 1,..., n. Пусть пометка вершины x на этом наборе принимает значение 1, тогда пометки y всех вершин, к которым из данной идут ребра, также на этом наборе принимают значение 1. Это следует из того, что каждому ребру соответствует какая-то дизъюнкция из двух литералов и хотя бы один из них должен на данном наборе обращаться в единицу.
Но отсюда следует, что пометки всех вершин любой строго связной компоненты должны одновременно обращаться в единицу на этом наборе. То есть в любой строго связной компоненте нет вершин, помеченных переменной и ее отрицанием.
Докажем теперь утверждение в другую сторону. Пусть в любой строго связной компоненте нет вершин, помеченных переменной и ее отрицанием. Покажем, что в этом случае существует набор 1,..., n (найденный за полиномиальное время), такой, что B выполняется на наборе 1,..., n.
Тот факт, что в любой строго связной компоненте нет вершин, помеченных переменной и ее отрицанием, означает, что в графе нет цепей в обоих направлениях между вершинами, помеченными x0 и x1. Предположим, что такой цепи нет в одном из этих направлений, например от x0 к x1. Тогда введение нового ребра от x1 к x0 не нарушит предположения о том, что в любой строго связной компоненте нет вершин, помеченных переменной и ее отрицанием. Действительно, если бы такая компонента появилась после введения нового ребра, то это новое ребро обязательно бы в нее входило, а, значит, между вершинами x0 и x1 были бы цепи в обоих направлениях. Но тогда одна из них, а именно: цепь из x0 к x1, существовала бы еще до введения нового ребра. Но это противоречит нашему предположению.
Повторяя эту процедуру ввода новых ребер, мы введем все возможные ребра от переменных к их отрицаниям. Так мы добьемся того, что в новом графе всегда будет цепь от переменной к ее отрицанию.
Теперь построим набор 1,..., n, на котором выполняется КНФ В. Для этого положим x=1, если существует ориентированный путь из x0 в x1, x=0 в противном случае. Очевидно, что такой набор строится за полиномиальное время. На нем КНФ обращается в единицу. Действительно, рассмотрим, например, дизъюнкцию xy. Покажем, что x и y не могут обращаться на данном наборе одновременно в 0. Пусть это не так. Тогда вспомним, что на этапе ввода новых ребер мы добились того, что существуют ориентированные пути из x1 в x0 и из y1 в y0. Но по построению графа G существуют ребра из x0 в y1 и из y0 в x1. Но это противоречит тому, что переменная и ее отрицание не входят в одну строго связную компоненту.
Теорема доказана.