§ 7. Комбинаторная мера информации. Вероятность искажения информации

В комбинаторной мере информации количество информации определяется как число комбинаций элементов (сочетаний символов). Количество информации совпадает с числом возможных сочетаний, перестановок и размещений элементов. Комбинирование символов в словах, состоящих только из 0 и 1, меняет значения слов. Рассмотрим две пары слов:

100110 и 001101 ;

011101 и 111010 .

В них произведена перестановка крайних разрядов (изменено местоположение знакового разряда в числе – перенесен слева направо ).

В теории кодирования имеет место понятие вероятности искажения информации. Понятие корректирующщей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки.

Пусть имеется п - разрядный код и вероятность искажения одного символа равна р. Число кодовых комбинаций, каждая из которых содержит k искажений символов, равна числу сочетаний из п по k :

.

Вероятность того, что искажены k символов, а остальные символов не искажены, определяется как . Тогда полная вероятность искажения информации определяется как

.

Глава ιіі. Теория графов

§ 1. Первоначальные понятия теории графов

Теория графов связана с проектированием вычислительных машин, комбинаторным анализом, служит математической моделью для всякой системы, содержащей бинарное отношение. Теория графов применяется при анализе функционирования сложных систем, таких как компьютерные и телефонные сети, сети железных дорог, ирригационные системы. Эта теория традиционно является эффективным аппаратом формализации задач экономической и планово-производственной практики, применяется в автоматизации управления производством, в календарном и сетевом планировании. В теории графов решалось много проблем, достойных внимания самых искушенных математиков. Основателем теории графов считается Леонард Эйлер, который доказал невозможность маршрута прохождения всех четырех частей суши в задаче о кенигсбергских мостах (1736 г.). Графы обладают эстетической привлекательностью благодаря их представлению в виде диаграмм.

Графом G называется совокупность множеств V и U, т.е.

G = < V, U > ,

где носитель V – множество вершин, а сигнатура U – множество дуг или ребер графа.

Дуга – линия с ориентацией, соединяющая две вершины графа.

Ребро – линия без ориентации, соединяющая две вершины графа.

Графы можно разбить на две большие группы: ориентированные (орграфы) и неориентированные графы.

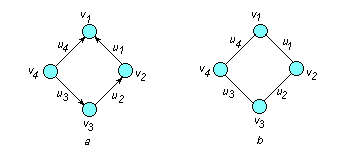
Рис. 4.1

Ориентированный граф G = < V, U > ( рис. 4.1a) имеет:

множество вершин ,

множество дуг .

В дуге v_i – начало дуги, v_j – конец дуги.

Неориентированный граф G = < V, U > (рис. 4.1b) имеет:

множество вершин ,

множество ребер .

Дуга (ребро) u , соединенная с вершиной v, называется инцидентной вершине v , а вершина v – инцидентной дуге (ребру) u.

Две дуги (ребра) называются смежными , если они инцидентны одной и той же вершине.

Две вершины графа называются смежными, если они соединены ребром (дугой).

Вершины графа могут быть соединены двумя и более ребрами или дугами:

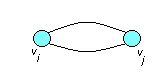
кратные ребра.

Граф, содержащий кратные ребра, называется мультиграфом.

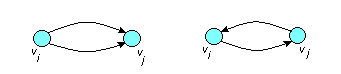
кратные дуги кратные дуги

(строго параллельные) (нестрого параллельные)

Число вершин графа называется его порядком.

Степенью s(v) вершины v называется число дуг (ребер) , инцидентных этой вершине.

Граф может иметь петли:

Петля дает в степень вершины вклад 2.

Если степень вершины равна нулю, то вершина называется изолированной, а если единице – висячей.

Граф, состоящий из одной изолированной вершины, называется тривиальным

Граф называется однородным степени k, если степени всех его вершин равны k.

Граф без петель и кратных ребер (строго параллельных дуг) называется простым графом, с петлями и кратными ребрами (строго параллельными дугами) – псевдографом .

Граф называется полным , если все его вершины попарно смежны.

Полный граф обозначают через К _п , где п – число вершин.

Пример. Задан ориентированный граф , у которого , . Является ли заданный граф G полным, однородным? Определить степень вершины v₂ .

□ Зная множество вершин V и множество дуг U, всегда можно построить граф G (рис. 4.2)

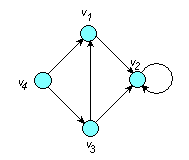
G

Рис. 4.2

Заданный граф G не является полным, т.к. не все вершины попарно смежны: вершины v₂ и v₄ не смежны. Граф G не является однородным, т.к. не все степени его вершин имеют одинаковое значение. Степень вершины v₂ равна 4, т.е. , т.к. этой вершине инцидентны две дуги и эта вершина имеет петлю. ■

Граф G называется двудольным, если множество его вершин V разбито на два непересекающихся подмножества V₁ и V₂ так, что каждое ребро (дуга) в G соединяет две вершины из разных подмножеств (рис. 4.3а).

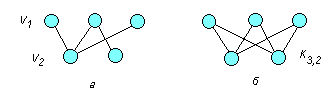
Рис. 4.3

Двудольный граф называется полным, если каждая вершина из V₁ соединена с каждой вершиной из V₂ и наоборот и обозначается K_m,n , где m – число вершин V₁ , а n – число вершин V₂ ( рис. 4.3б ).

Граф К_т,п имеет т + п вершин и т·п ребер. Граф К _1,п называется звездным графом.

Граф является частью графа , если . Часть графа может совпадать с самим графом G (также как в теории множеств ).

Граф, полученный из графа G удалением некоторых вершин и инцидентных им дуг (ребер) называется подграфом графа G .

Подграф, содержащий все вершины графа, называется остовным подграфом.

Подграф также является частью графа.

Множество вершин, смежных с вершиной , называется ее окрестностью (окрестностью единичного радиуса, сечением) и обозначается Г . Тогда граф G можно определить как совокупность множества вершин и множества их окрестностей, т.е.

.

Пример. Определить окрестность вершины v₃ графа, изображенного на рисунке

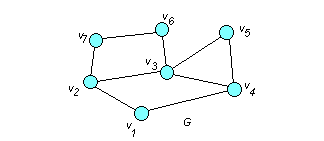
□ Смежными с вершиной v₃ являются вершины v₂ , v₄ , v₅ , v₆ .

Поэтому Гv₃ = { v₂ , v₄ , v₅ , v₆ }. ■

Два графа G и G₁ называются изоморфными, если между множествами их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг также должна быть одинаковой.

Другими словами, графы G и G₁ изоморфны, если для них сохраняется отношение инцидентности .

Пример. Показать, что графы G и G₁ ( рис. 4.4 ) изоморфные.

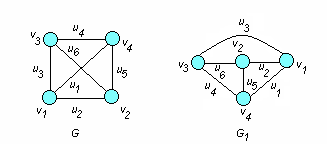
Рис. 4.4

□ Проверим для этих графов сохранение отношения инцидентности.

Граф G :

вершина v₁ инцидентна ребрам u₁, u₂, u₃ ;

вершина v₂ инцидентна ребрам u₂, u₅, u₆ ;

вершина v₃ инцидентна ребрам u₃, u₄, u₆ ;

вершина v₄ инцидентна ребрам u₁, u₄, u₅ .

Граф G₁ :

вершина v₁ инцидентна ребрам u₁, u₂, u₃ ;

вершина v₂ инцидентна ребрам u₂, u₅, u₆ ;

вершина v₃ инцидентна ребрам u₃, u₄, u₆ ;

вершина v₄ инцидентна ребрам u₁, u₄, u₅ .

Отношение инцидентности выполняется, значит, графы G и G₁ изоморфны. ■

Очевидно, что отношение изоморфизма графов является отношением эквивалентности, т.е. оно рефлексивно, симметрично и транзитивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.

Если сопоставить каждой вершине графа вес w_i из множества весов W, то получим множество взвешенных вершин

.

Если сопоставить каждой дуге графа G = < V, U > вес p_i из множества весов Р, то получим множество взвешенных дуг

.

Совокупность множества взвешенных вершин и множества взвешенных дуг определяет взвешенный граф .

Аналогично определяется взвешенный неориентированный граф.

Совсем не обязательно, чтобы были взвешены одновременно вершины и дуги (ребра) графа. В качестве весов могут использоваться какие-либо числа, переменные, функциональные переменные.