Распределение предприятий по уровню рентабельности

Рентабельность, %	Количество предприятий
10 12 15 17 20	1 2 3 2 2
Итого	10

Теперь мы применили формулу средней арифметической взве­шенной:

где f_i - частота, т.е. число раз, которое встречается каждое значение приз­нака.

Часто данные наблюдения представляют в интервальной фор­ме. Тогда при расчете средней в качестве х_i берут сере­дины интервалов. Если первый и последний интервалы открытые (не имеют одну из границ), то их условно «закрывают», принимая за величину интервала величину примыкающих интервалов, т.е. первый закрывают исходя из величины второго, последний — предпоследнего.

Так, в ниже приведенном примере.1 середина первого интервала равна 500 (ве­личина второго интервала: 1000 (2000-1000); тогда нижняя гра­ница первого: 0 (1000-1000), а середина - 500. Аналогично по­ступаем с последним интервалом. За его середину принимаем 25000 (величина предпоследнего интервала 10000 (20000-10000), тогда верхняя граница последнего 30000 (20000+10000), а середи­на последнего соответственно — 25000).

Если веса представлены не частотами, а частостями, формула для расчета средней арифметической взвешенной модифициру­ется в следующую:

где .

частость, которая представляет собой удельный вес частоты соответствующей варианты в общей сумме частот; сумма частостей для расчетов по данной формуле должна быть равна 1, т.е. в долях от единицы, а не в процентах.

6.1. По результатам выборочного обследования одной из групп населения рассчитаем среднедушевой размер денежного дохода (данные условные).

Таблица 6.3

Среднедушевой денежный доход, руб./мес.	Доля населения, %	Середины интервалов xi	Частость wi
До 1000	4,1	500	0,041
1000 - 2000	8,6	1500	0,086
2000 - 4000	12,9	3000	0,129
4000 - 6000	13,0	5000	0,130
6000 - 8000	10,5	7000	0,105
8000 - 0000	27,8	9000	0,278
10000 - 20000	12,7	15000	0,127
20000 и выше	10,4	25000	0,104
И т о г о	100,0	-	1,000

Тогда среднедушевой размер месячного дохода составит

= 500 • 0,041 + 1500 • 0,086+3000 • 0,129+5000 • 0,13+7000 • 0,105+ +9000 • 0,278+15000 • 0,127+25000• 0,104 = 8928,5 руб.

Средняя арифметическая величина обладает рядом математи­ческих свойств. Основные из них состоят в следующем:

1. Если x_i = с, где с — постоянная величина, то средняя арифметическая будет равна с.

2 . Сумма отклонений значений признака от его средней арифметической равна 0, т. е.

3 . Если из всех значений признака вычесть постоянную величину с, то средняя арифметическая уменьшится на эту величину с:

4. От уменьшения или увеличения частот f_i - каждого значе­ния признака в т раз величина средней арифметической не изменится:

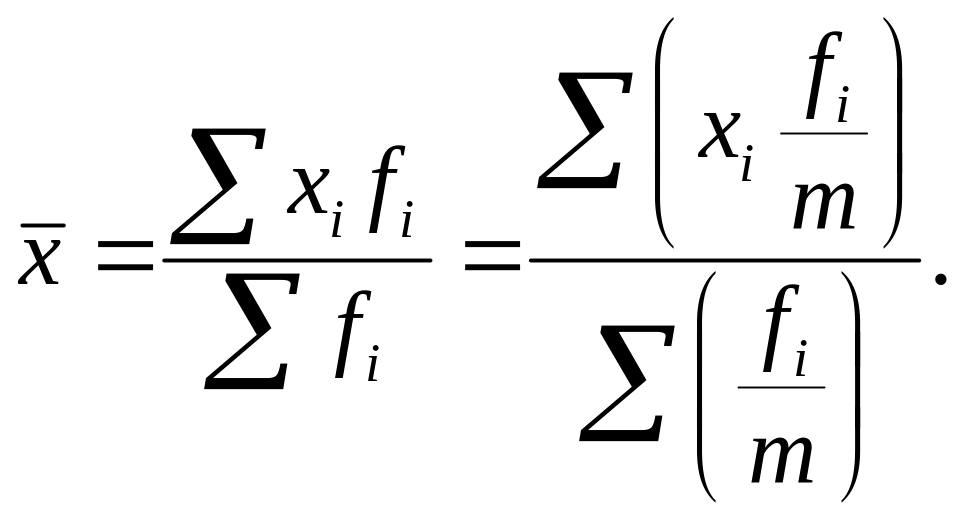
5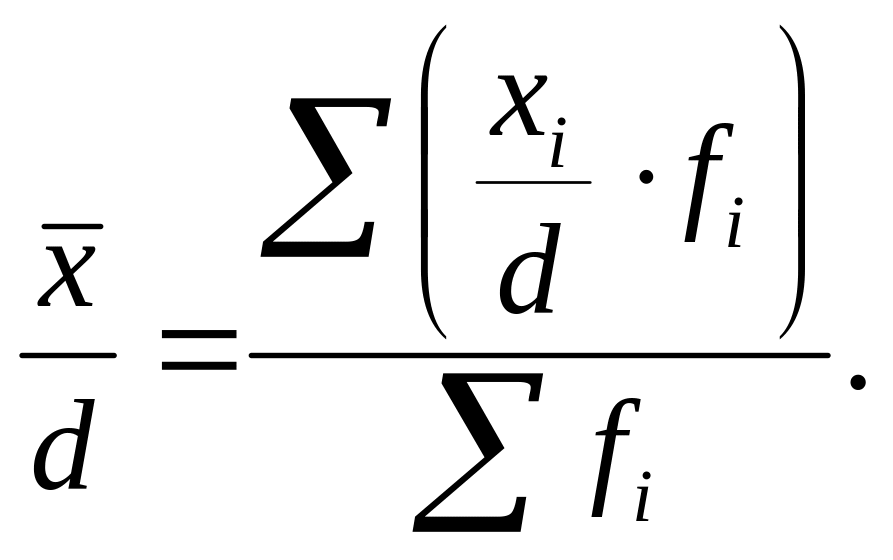 . Если все индивидуальные значения признака уменьшить или увеличить в d раз, то величина средней арифметической так­же уменьшится или увеличится в d раз:

На изложенных свойствах средней арифметической базируется один из методов ее расчета - способ моментов, или метод отсчета от условного нуля, который используется в случае вариационных рядов с равными интервалами. Согласно этому методу среднюю арифметическую взвешенную можно вычислить по следующей формуле

где 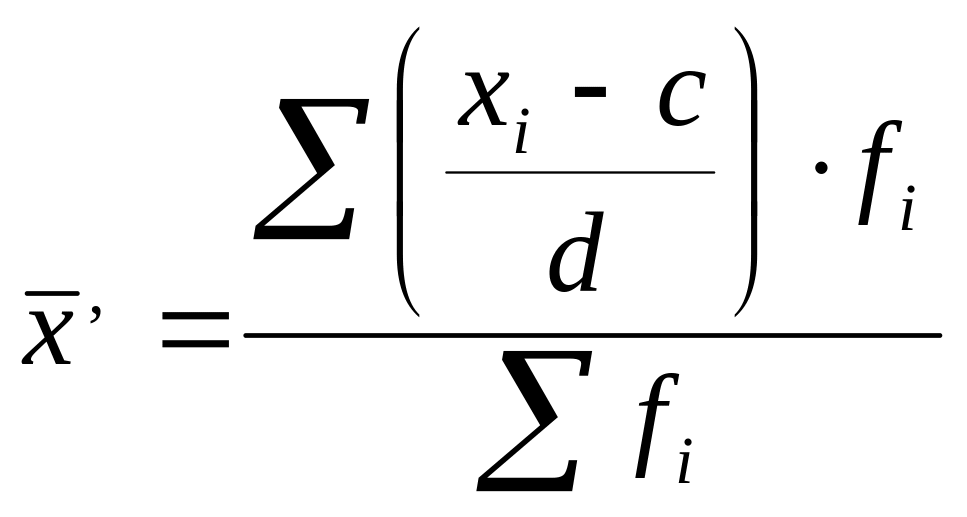- момент первого порядка.

За d, как правило, принимают величину интервалов, а за с – значение середины интервала, находящегося в центре ряда (если количество интервалов нечетное) или середину интервала с наибольшей частотой также из центра ряда (при четном количестве интервалов в центре ряда будут находиться два интервала).

6. 2. Рассчитаем среднюю за период прибыль по группе банков способом моментов :

Таблица 6.4

Прибыль, тыс.д.е.	Середина интервала xi	Количество банков f	xi – с с = 3750	d = 1500
До 1500	750	6	-3000	-2	-12
1500 – 3000	2250	5	-1500	-1	-5
3000 – 4500	3750	9	0	0	0
4500 – 6000	5250	4	1500	1	4
6000 и выше	6750	2	3000	2	4
С у м м а	-	26	0	0	-9

П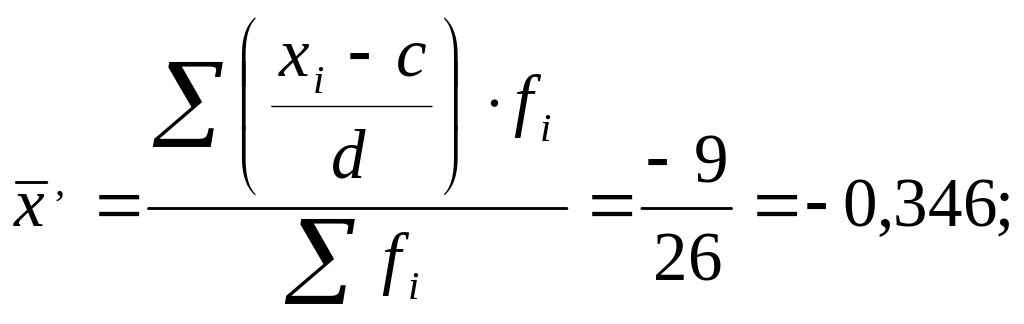 роведем расчет:

x = x' ∙ d + c = -0.346 ∙ 1500 + 3750 = 3230,769 тыс.д.е.

Средняя гармоническая

Средняя гармоническая взвешенная величина является модифици­рованной формой средней взвешенной арифметической. Она применяется в тех случаях, когда не знают значения частот у ва­риант ряда, зато известны для каждого х₍ произведения этих вари­ант на соответствующие им частоты, т.е.: F_i = х_i ∙ f_i. Величиной F_i может быть, например, товарооборот по видам товаров при рас­чете средней их цены; фонды заработной платы у отдельных ка­тегорий работников при расчете средней заработной платы; сто­имостные объемы сделок при покупке валют, ценных бумаг, бир­жевых продажах и т.д. Как видим, ситуаций, когда нам известны не частоты, а произведения частот на соответствующие им вари­анты при расчете средней величины, более чем достаточно.

Формула средней гармонической имеет вид:

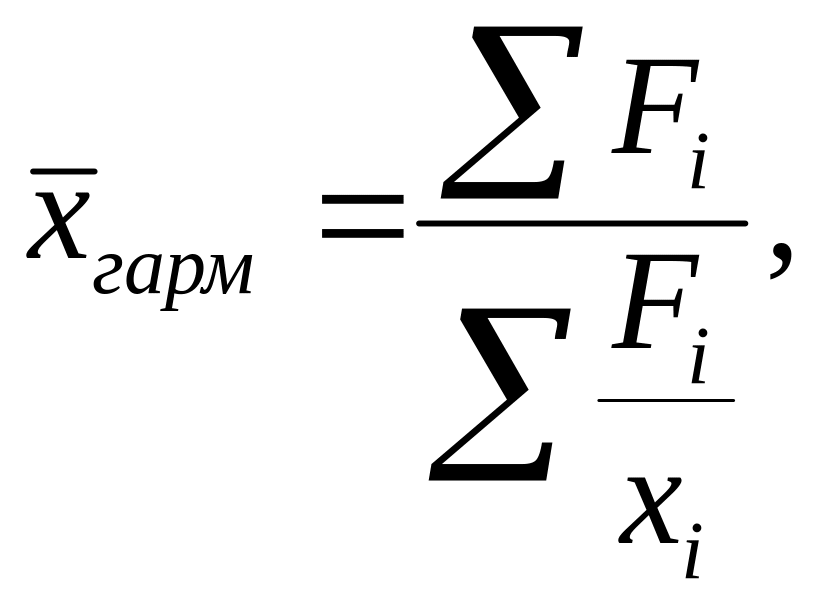
где F_i – значение произведения варианты на соответствующую ей частоту;

x_i - значения вариант.

Если для каждой варианты мы рассчитаем частоту как то формула

с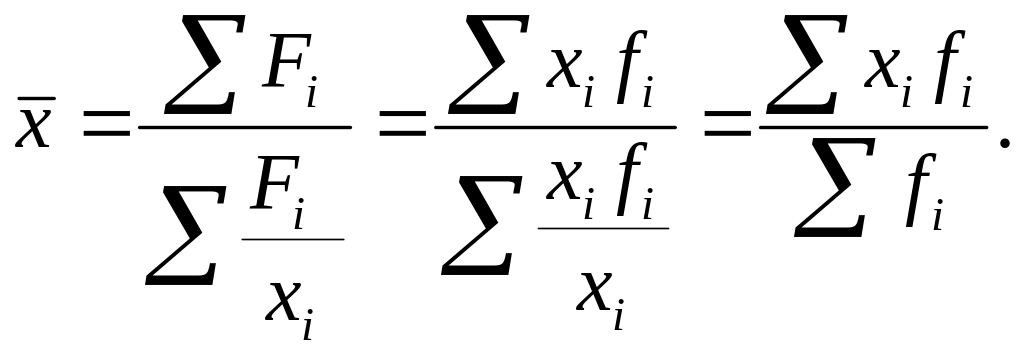 редней гармонической взвешенной превратится в формулу для расчета средней арифметической взвешенной:

6. 3. По данным о ценах акций и уровнях капитализации рассчитаем среднюю цену одной акции:

Таблица 6.5

Вид акции	Цена за одну акцию, тыс.руб. Xi	Капитализация *, тыс.руб. Xi ∙ fi = Fi
А	1,0	500
Б	2,3	1840
В	1,8	1314
Г	2,7	2565
Д	1,4	854
И т о г о	-	7073

Примечание. * Капитализация представляет собой общую стоимость продаж акций определенного вида, математически она равна произведению цены за одну акцию на объем их продаж.

Средняя цена по группе акций:

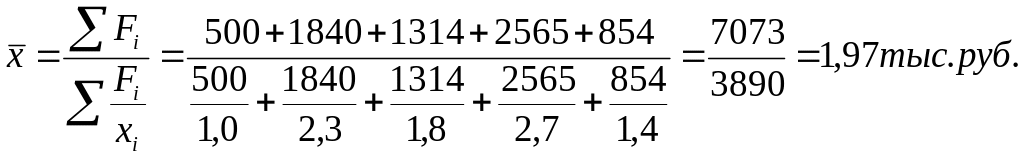
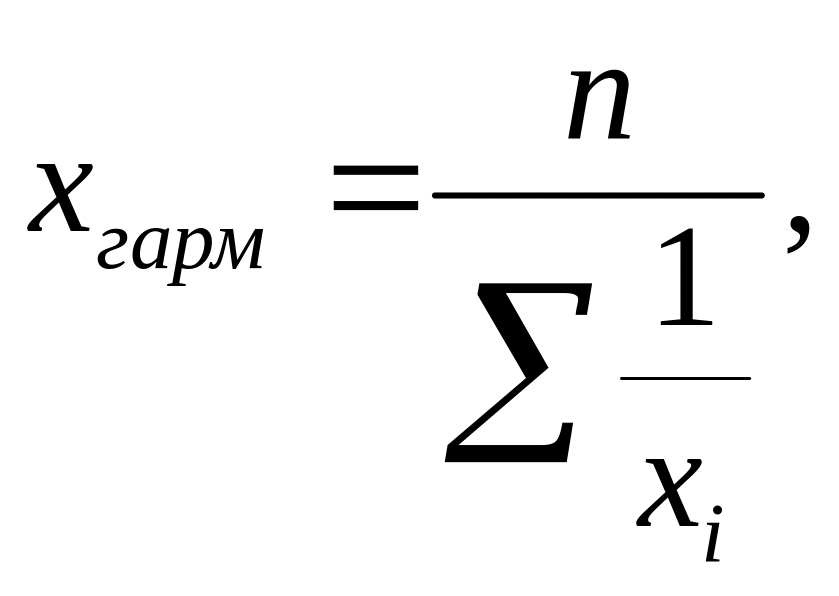Если произведения вариант на соответствующие им частоты равны между собой (при этом мы можем их не знать, но известно об их равенстве), т.е. F₁ = F₂ = F₃ =…= F_i, то применяется средняя гармоническая простая, рассчитываемая по следующей формуле

где n – число единиц в совокупности.

6. 4.Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно - со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w₁=w₂ (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч.

Средняя геометрическая

Если минимальное и максимальное значения признака резко от­личаются друг от друга, что возникает при существенной вариации показателя в совокупности, либо, если мы имеем данные, представляющие собой отношения двух показателей, например, ин­дексы или коэффициенты роста, то для нахождения среднего значения используется формула средней геометрической, Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая

где n – число единиц в совокупности.

Д ля сгруппированных данных с неравными частотами приме­няется средняя геометрическая взвешенная

Предприятиями были осуществлены следующие инвестиции в основные фонды:

Таблица 6.6

Номер предприятия	Инвестиции в основные фонды, тыс. руб.
1	10
2	40
3	76
4	130
5	274
6	550
7	1080
8	2300
9	5100
Итого	9560

Найдем средний размер инвестиций. Поскольку колебле­мость признака довольно значительная и данные несгруппированы, воспользуемся формулой средней геометрической простой:

Средняя квадратическая и другие степенные средние более высоких порядков

Если мы подставим в формулу средней степенной т = 2, то полу­чим среднюю квадратическую:

взвешенную (для сгруппированных данных):

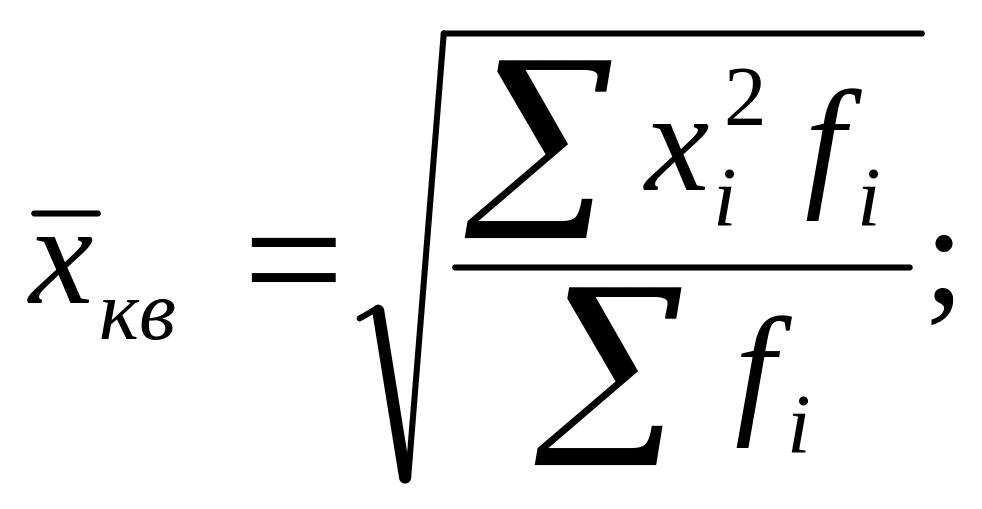
простую (для несгруппированных данных):

Средняя квадратическая величина широко применяется при оценке вариации признака, а также в многомерных статистичес­ких методах. Кроме того, прикладное значение имеет расчет сте­пенных средних и более высоких порядков, например, при изуче­нии характеристик распределения случайных величин. Формулы для их вычисления получаются при подстановке в качестве т соот­ветствующего показателя степени.

Мода.

Мода (Мо) - это наиболее часто встречающееся значение призна­ка, или, говоря иначе, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному. В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды.

В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, ко­торому соответствует наибольшая частота, и будет значением моды.

6. 5. По представленным результатам проведения экзамена по статистике определим моду.

Таблица 6.7

Балл (по 5-балльной системе)	Число студентов
2	3
3	10
4	7
5	4

Здесь наибольшая частота – 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами на экзамене, была "тройка".

Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, ко­торым является интервал с наибольшей частотой, а затем ведут расчет по формуле

где x_Mo- нижняя граница модального интервала;

d - величина интервала;

f_Mo – частота модального интервала;

f_Mo-1 – частота интервала, предшествующего модальному;

f_Mo+1 – частота интервала, следующего за модальным.

6. 6. Имеются данные по группе банков.

Таблица 6.8

Сумма выданных кредитов, млн.д.е.	Количество банков
До 40	8
40 – 60	15
60 – 80	21
80 – 100	12
100 – 120	9
120 – 140	7
140 и выше	4

Определим модальный размер выданных кредитов:

1. модальным является интервал 60—80, так как ему соответ­ствует наибольшая частота (21);

2. нижняя граница модального интервала х_Мо = 60; величина интервала d = 20 (80 - 60 = 20);

частота модального интервала f_Мо = 21; частота интервала, предшествующего модальному, f_Мо-1= 15; частота интервала, следующего за модальным, f_Мо+1 = 12.

Тогда, подставив в формулу соответствующие величины, по­лучим:

Если интервалы вариационного ряда не равны между собой, то для определения моды необходимо проделать следующие действия;

1) для каждого интервала на основе частот (f_i) и длин интерва­лов (d_i) рассчитать величину которая называется абсолютной плотностью распределения;

2. по наибольшей абсолютной плотности распределения най­ти модальный интервал;

3. определить значение моды по формуле

где x_Mo – нижняя граница модального интервала;

d_Mo – величина модального интервала;

р_Мо - абсолютная плотность модального интервала;

p_Mo-1 – абсолютная плотность интервала, предшествующего модальному;

p_Mo+1 – абсолютная плотность интервала, следующего за модальным.

6. 7. Имеются данные по группе коммерческих банков :

Таблица 6.9

Кредитная ставка по краткосрочным кредитам, % хi	Количество банков fi	Величина интервала di	Абсолютная плотность распределения
10 – 15	4	5	0,80
15 – 25	3	10	0,30
25 – 40	14	15	0,93
40 – 55	10	15	0,67
55 - 65	6	10	0,60

Определим модальное значение размера кредитной ставки под краткосрочные кредиты.

М одальным является интервал 25-40, так как у него наиболь­шая плотность распределения (0,93). Значение моды равно: