Алгоритм нахождения общего решения

1. Составить характеристическое уравнение ^k – a₁^k–1 – … – a_k–1 – a_k = 0.

2. Найти все его различные корни ₁ , … , _s и их кратности r₁ , … , r_s .

3. Записать общее решение u(n, c₁ , … , c_k) = .

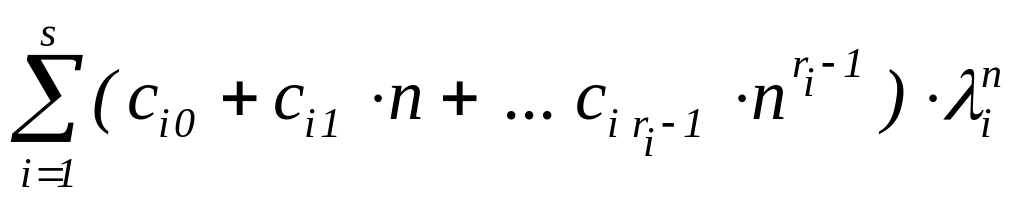Если нужно найти частное решение u(n) с заданными начальными условиями u(0)=u₀ , … , u(k–1)=u_k–1 , то составляем систему линейных уравнений:

,

из которой однозначно находятся все k констант с_ij (0  i  s, 0  j < r_i). Можно доказать (как ?!), что эта система всегда однозначно разрешима.

Примеры: 1. Найти общее решение линейного рекуррентного соотношения f(n + 3) = 3f(n + 2) – 3f(n + 1) + f(n).

Составляем характеристическое уравнение: ³–3²+3–1 = ( – 1)³ = 0. Оно имеет единственный корень  = 1 кратности r = 3. Значит, общее решение этого соотношения третьего порядка выглядит так: u(n, c₀ , c₁ , c₂) = (c₀ + c₁n + c₂n²)1ⁿ = c₀ + c₁n + c₂n² .

Если требуется соблюсти начальные условия u(0) = 0, u(1) = 1, u(2) = 3, то получается система

,

из которой находим c₀ = 0, c₁ = = c₂ , т.е. u_n = .

2. Найти общее решение линейного рекуррентного соотношения

f(n+3) = –f(n+2) – 2f(n+1) + 16·f(n).

С

_ ³ + ² + 2· – 16 |  – 2

³ – 2·² ² + 3· + 8

_ 3·² + 2· – 16

3·² – 6·

_ 8· – 16

8·

 – 16

0

оставляем характеристическое уравнение: () = ³ + ² + 2 – 16 = 0. Угадываем корень ₁ = 2 и понижаем степень уравнения, деля характеристический многочлен на  – 2. Таким образом, ³ + ² + 2 – 16 = ( – 2)·(² + 3· + 8), и решая уравнение ² + 3· + 8 = 0, находим остальные корни уравнения _{2 , 3} = .

Все корни различны, т.е. имеют кратности r₁ = r₂ = r₃ = 1. Поэтому общее решение таково: u_n = 2ⁿ·a + ·b + ·c (a, b, c  C).

3. Найти общее решение линейного рекуррентного соотношения

f(n+4) = –2·f(n+2) – f(n).

Характеристическое уравнение () = ⁴ + 2·² + 1 = 0 раскладывается на множители ⁴ + 2·² + 1 = (² + 1)², так что имеет два корня ₁ = i, ₂ = –i кратностей r₁ = 2 = r₂ . Общее решение записывается так:

u_n = iⁿ·(a·n + b) + (–i)ⁿ·(c·n + d).

§ 5. Частные решения линейных неоднородных рекуррентных соотношений с постоянными коэффициентами и специальной правой частью

Теорема (о частном решении линейного неоднородного рекуррентного соотношения). Для любого линейного рекуррентного соотношения с постоянными коэффициентами

f(n + k) = a₁f(n + k – 1) + …+ a_kf(n) + T_m(n)ⁿ,

где T_m(x) – многочлен степени m,   С, существует решение вида n^rS_m(n)ⁿ , где S_m(x) – некоторый многочлен степени m, а r – кратность корня  в характеристическом уравнении x^k – a₁x^k–1 – … – a_k–1x – a_k = 0 . В частности, если  не является корнем характеристического уравнения, то нужно считать r = 0.

Доказательство. Подставим n^r(s_mn^m+…+s₁n+s₀)ⁿ в рекуррентное соотношение:

(здесь всегда можно считать m > r, используя, если необходимо, нулевые коэффициенты многочленов).

В случае, когда  не является корнем характеристического многочлена, т.е. r = 0, система упрощается:

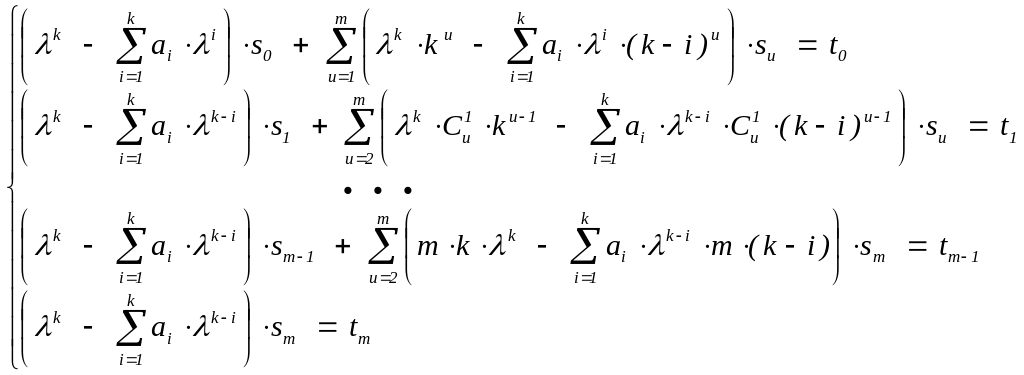
Видно, что система имеет верхнетреугольный вид с диагональными элементами ()  0, а потому имеет единственное решение.

Если же  – это r-кратный корень характеристического многочлена (x), то в силу леммы о соотношениях для r-кратного корня многочлена последняя группа уравнений системы тривиальна: все коэффициенты в ней нулевые. Действительно, эти коэффициенты имеют вид , где u = m+j–r (j = 1, … , r).

При этом

по упомянутой выше лемме.

Более того, система снова верхнетреугольная. В самом деле, если j > u, то коэффициент при s_u в j-м уравнении первой группы (j  r) равен

по лемме о соотношениях для r-кратного корня многочлена, т.к. u+r–j < r при j > u. При j = u коэффициент при s_u равен

и отличен от нуля по той же лемме.

Если же j > r, то коэффициенты могут быть ненулевыми только для значений u из диапазона j–r  u  m. При этом

по лемме о соотношениях для r-кратного корня многочлена, т.к. u+r–j < r при j > u. При j = u > r коэффициент при s_u равен и отличен от нуля по той же лемме.

Таким образом, в любом случае полученная система уравнений крамерова и имеет единственное решение.

Теорема доказана.

Эта теорема упрощает нахождение частных решений для линейных рекуррентных соотношений с постоянными коэффициентами, имеющими свободные члены специального рассмотренного в теореме вида.

Пример. 1. Найти формулу общего члена решения рекуррентного соотношения f(n + 3) = f(n) + 1.

Здесь (x) = x³ – 1 имеет три простых корня ₁ = 1, , а свободный член соотношения представим в виде 1 = ₁ⁿT₀(x), где T₀(x) = 1. Таким образом, общее решение однородного соотношения записывается в виде c₁₁ⁿ + c₂₂ⁿ + c₃₃ⁿ, а частное решение неоднородного соотношения – в виде cn₁ⁿ = cn. Подставляя это выражение в исходное соотношение, получаем соотношение с(n+3) = cn + 1, откуда находим c = .

Таким образом, общее решение рассматриваемого неоднородного соотношения имеет вид c₁₁ⁿ + c₂₂ⁿ + c₃₃ⁿ + .

2. Найти формулу общего члена решения рекуррентного соотношения

f(n + 1) = f(n) + n² – 1.

Здесь () =  – 1 имеет единственный корень  = 1, так что общее решение однородного соотношения (n, c) = c.

Частное решение неоднородного соотношения будем искать в виде n·(s₂n²+s₁n+s₀)1ⁿ, т.к. свободный член рассматриваемого соотношения имеет вид 1ⁿT₂(n), где T₂(x) = x² – 1. Подставляя это выражение в исходное соотношение, получим

s₂(n + 1)³+s₁(n + 1)²+s₀(n + 1) = s₂n³ + s₁n² + s₀n + n² – 1,

т.е. 3s₂n²+(3s₂ + 2s₁)n + s₂ + s₁+s₀ = n² – 1, откуда , а значит, s₂ = , s₁ = – , s₀ = – . Таким образом, общее решение рассматриваемого неоднородного соотношения имеет вид

w(n) = с + ( n³ – n² – n).