12. Модель 13."Выход в космос"

Рассмотрим движение некоторой планеты вокруг массивной звезды, которую будем считать неподвижной¹. Влиянием других звезд и планет на движение рассматриваемой планеты пренебрежем. Исследуем возможные орбиты движения планеты.

Звезда и планета взаимодействуют с силой, подчиняющейся закону всемирного тяготения Ньютона. Эта сила взаимодействия является консервативной и направлена вдоль линии, соединяющей центры звезды и планеты. Поэтому в процессе движения планеты будут сохраняться механическая энергия и момент импульса. Так как момент импульса является вектором, то орбита планеты будет плоской.

Введем систему координат в плоскости орбиты, начало отсчета которой совместим с центром звезды (рис. 13.1). Положение планеты удобно задавать с помощью полярных координатах: - расстояние от начала координат до планеты, - полярный угол между осью и направлением на планету. Вектор скорости планеты разложим на две составляющих - радиальную , направленную вдоль линии, соединяющей планету со звездой, и перпендикулярную ей азимутальную компоненту .

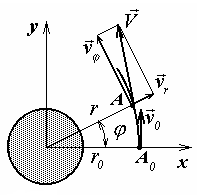
Рис. 13.1

Будем считать, что в начальный момент времени планета находилась на оси в точке на расстоянии от звезды, и ее скорость была равна и направлена перпендикулярно оси . Заметим, что в этой точке радиальная компонента скорости , поэтому в этой точке расстояние до звезды минимально или максимально. Выбором направления осей координат всегда можно добиться такого положения, поэтому введенные начальные условия не являются специальными. Закон сохранения механической энергии записывается в виде уравнения:

, (13.1)

где - массы планеты и звезды, соответственно; - гравитационная постоянная; - потенциальная энергия гравитационного взаимодействия.

Сохранение момента импульса выражается уравнением:

. (13.2)

Выразим из уравнения (13.2) азимутальную составляющую скорости:

(13.3)

и подставим в уравнение (13.1):

. (13.4)

Теперь очень внимательно посмотрите на полученное уравнение² - это уравнение не содержит угловой координаты , только расстояние и радиальную составляющую скорости . Более того, по форме оно совпадает с уравнением закона сохранения энергии для тела, движущегося вдоль одной оси:

, (13.5)

поэтому для его анализа можно пользоваться стандартными методами, основанными на исследовании потенциальной кривой. В данном случае потенциальная кривая описывается функцией:

(13.6)

С физической точки зрения эта функция не является потенциальной энергией, так как первое слагаемое является частью кинетической энергии. Однако по своей математической форме в уравнении (13.4) эта функция играет смысл потенциальной энергии, поэтому эту функцию называют «эффективной потенциальной энергией».

Прежде чем приступить к качественному анализу уравнения (13.4), как всегда, введем собственную систему единиц измерения, дабы избавится от лишних параметров. В качестве единицы длины выберем начальное расстояние . Второй «основной» единицей сделаем скорость движения планеты по круговой орбите радиуса . Эту скорость можно найти из очевидного уравнения, следующего из второго закона Ньютона:

(13.7)

Таким образом, единица скорости определяется соотношением:

. (13.8)

Заметим, что единицей времени в данной системе единиц является величина:

, (13.9)

а период обращения по круговой орбите в данной системе единиц равен . Эта величина нам понадобится для численного решения уравнений движения.

Выразим физические величины через введенные единицы измерений и безразмерные («штрихованные», по нашей терминологии) величины

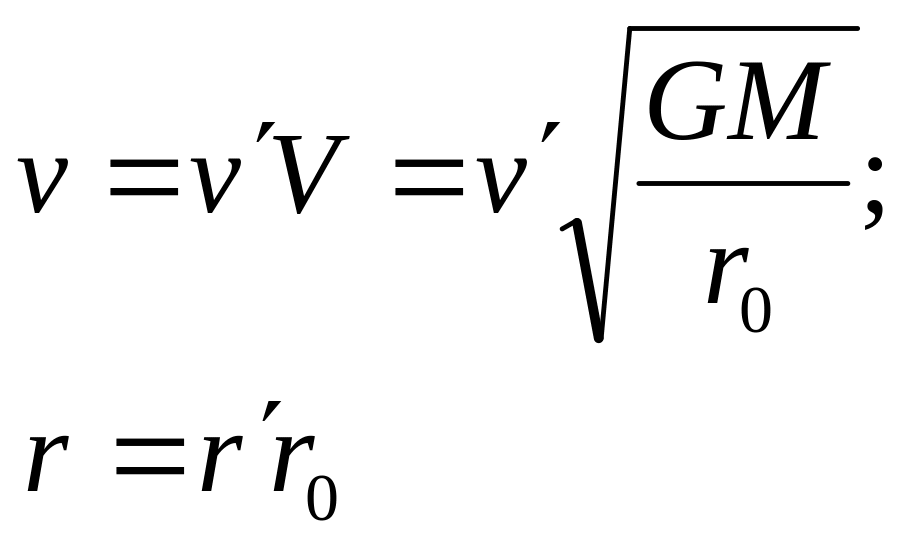(13.10)

и подставим их в уравнение (13.4). После сокращения и отбрасывания штрихов получаем уравнение:

, (13.11)

содержащее всего один параметр начальную скорость (естественно в относительных единицах). Для того, чтобы иметь возможность построить траекторию движения, перепишем закон сохранения момента импульса в виде (используя введенные единицы):

, (13.12)

где - угловая скорость вращения радиус-вектора планеты. Выбрав в качестве единицы измерения величину начального расстояния, мы стандартизировали и начальные условия, положив начальное расстояние равным единице.

Получим также динамическое уравнение, описывающее радиальное ускорение планеты. Для этого вычислим производную по времени от уравнения (13.11)

(13.13)

При вычислении производной использовано правило дифференцирования сложной функции. Учитывая, что , последнее уравнение запишем в форме, традиционной для второго закона Ньютона:

. (13.14)

В первом слагаемом правой части уравнения без труда можно узнать силу гравитационного притяжения. Второе слагаемое является производной от эффективной части потенциальной энергии. Однако ему можно дать и более традиционное толкование - это центробежная сила инерции, появляющаяся во вращающихся системах отсчета³. Это уравнение лучше поддается численному решению, чем уравнение закона сохранения механической энергии. Дело в том, что если из уравнения (13.11) выразить значение скорости, то неизбежно появляются два знака скорости, поэтому при программировании возникают трудно решаемые проблемы правильного выбора знака, который постоянно будет меняться в ходе движения планеты.

Мы уже убедились, что можно проанализировать возможные типы движений системы по виду потенциальной кривой. В нашем случае эффективная потенциальная энергия определяется функцией (13.6), которая в используемой системе единиц имеет вид:

. (13.15)

Если⁴ , то эта при , а при , причем . Следовательно, данная функция имеет точку минимума, то есть очередной раз мы «попадаем» в потенциальную яму. Эффективная потенциальная энергия зависит от начальных условий, поэтому у нас нет возможности независимо варьировать потенциальную кривую и начальные условия. Это упрощает анализ - мы имеем только один варьируемый параметр - начальную скорость. Следовательно, одной потенциальной кривой соответствует одна траектория. В наших единицах начальное расстояние равно 1, поэтому полная энергия равна эффективной потенциальной энергии при . Это позволяет сразу провести на графике потенциальной энергии уровень полной энергии. Чтобы не загромождать график, этот уровень проведем мысленно.

Допустим (какая наглость!) Ньютон не прав. Закон всемирного тяготения Ньютона утверждает, что сила гравитационного притяжения обратно пропорциональна квадрату расстояния. А может этот показатель степени немного отличается от двойки? Посмотрим, что произойдет с орбитой планеты, если мы незначительно изменим закон всемирного тяготения. Положим, что сила притяжения определяется формулой (мы по-прежнему пользуемся собственной системой единиц):

, (13.16)

где - некоторая малая добавка.

Этой силе соответствует потенциальная энергия, определяемая функцией:

. (13.17)

В компьютерной программе необходимо изменить не только выражение для силы, но и процедуру контроля точности решения (именно для этого мы привели выражение для энергии).

Рассмотрим движение планеты в системе двух звезд. Как известно, существует множество систем двойных, тройных и т.д. звезд. Некоторые астрономы утверждают, что в двойных системах возможно существование обитаемых планет. Интересно, какой хоровод звезд-двойняшек увидят обитатели этой планеты на своем небе.

Давайте исследуем траектории движения планеты в гравитационном поле двух одинаковых звезд. Примем, что масса планеты значительно меньше масс звезд, поэтому движение планеты никак не влияет на движение звезд. Для простоты, будем полагать, что звезды движутся по круговым орбитам вокруг общего центра масс. Также будем полагать, что все тела движутся в одной плоскости.

Иными словами, попытаемся взглянуть на эту систему глазами стороннего наблюдателя. Мы рассчитаем орбиту планеты в системе отсчета, связанной со звездами, а переход в «планетарную» систему отсчета пусть проводят местные астрономы.

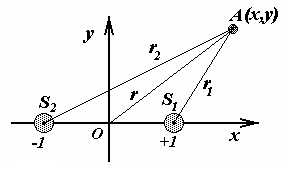
Рис. 13.2

Свяжем декартовую систему координат со звездами , так что ось совпадает с линией, их соединяющей, а ось проходит через середину отрезка (рис. 13.2). Надеюсь, вы уже привыкли пользоваться в каждой задаче собственной системой единиц, поэтому для вас не должно быть удивительно, если координаты звезд окажутся равными . Также будем считать, что силы гравитационного притяжения планеты к звезде выражается формулой:

, (13.18)

где - расстояние от планеты до соответствующей звезды.

Рекомендуем самостоятельно разобраться с системой единиц, в которой справедлива формула (13.18).

В этом разделе не будем мудрствовать с записью уравнений движения в полярных координатах, поэтому положение планеты будем описывать парой привычных декартовых координат . Это упростит запись уравнений движения, но усложнит их анализ и решение. Смиримся с этим обстоятельством, и основные усилия направим на компьютерное моделирование движения планеты.

В основание модели положим уравнение второго закона Ньютона⁵:

, (13.19)

которое в проекциях на оси координат записывается в виде системы уравнений:

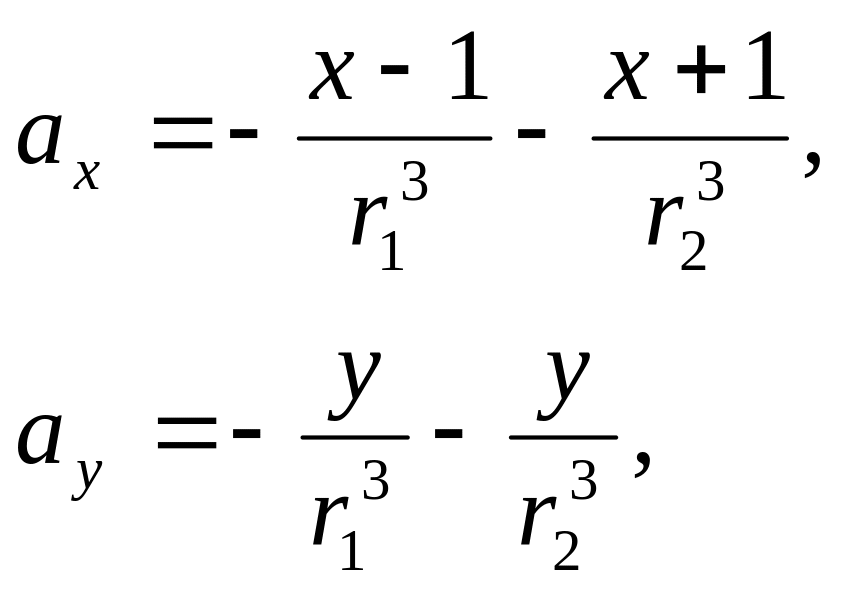(13.20)

где

В качестве начальных условий необходимо задавать как начальное положение планеты , так и ее начальную скорость .

Модель (13.20) страдает существенным недостатком - в ней не учтено движение самих звезд - без их вращения вокруг общего центра масс расстояние между звездами не может оставаться постоянным. Если звезды не будут двигаться, они просто упадут друг на друга. Можно, конечно, предположить, что система отсчета связана с вращающимися звездами, однако, в таком случае эта система является неинерциальной, поэтому в уравнениях движения должны появиться силы инерции - центробежная и сила Кориолиса⁶.

Оценим, при каких условиях можно пренебречь центробежной силой. Итак, пусть звезды вращаются по круговым орбитам, радиуса (здесь используем систему СИ, в нашей же системе единиц ). Тогда расстояние между звездами равно . Для определения угловой скорости звезд , запишем уравнение второго закона Ньютона для одной из них:

, (13.21)

где - масса звезды. Из этого равенства получаем:

. (13.22)

Центробежная сила, действующая на планету, рассчитывается по формуле ( масса планеты, - расстояние до оси вращения), поэтому условие допустимости пренебрежения этой силой записывается в виде неравенства (сравниваем с гравитационными силами, действующими на планету):

. (13.23)

Используя выражение (13.22), получаем необходимые условия:

, (13.24)

которые в реальности неосуществимы. Действительно, для их выполнения планета должна двигаться где-то очень близко от центра масс звезд ( ). Если одно из неравенств выполняется (например, планета близка к одной из звезд ), то второе выполнятся заведомо не будет. Следовательно, нужно обязательно учитывать силы инерции. А жаль, больно уж очень красивые траектории получаются при решении⁷ системы (13.20). Нам они так нравятся, что не жалко отвести на их изображение почти страницу (рис. 13.3). Первые четыре «картинки» (1 а-г ) показывают несколько стадий траектории 1. Разные траектории (1-4) соответствуют разным начальным условиям и только!

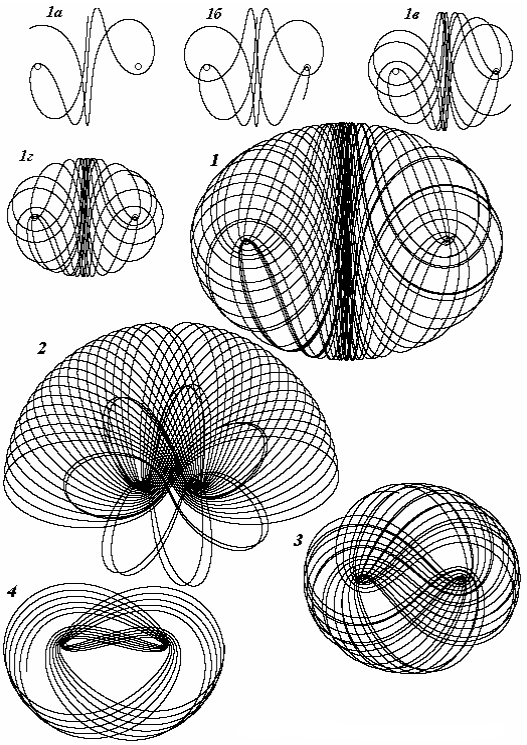
Рис. 13.3

Для того, чтобы получить систему уравнений в системе отсчета, связанной со звездами, в уравнения (13.20) необходимо добавить центробежную силу , направленную вдоль линии, соединяющей начало координат с планетой, и силу Кориолиса . Проекции силы Кориолиса на оси вращающейся системы определяются по формулам:

.

В нашей системе единиц и , следовательно .

Таким образом, уравнения движения планеты в неинерциальной системе отсчета, связанной со звездами, имеют вид:

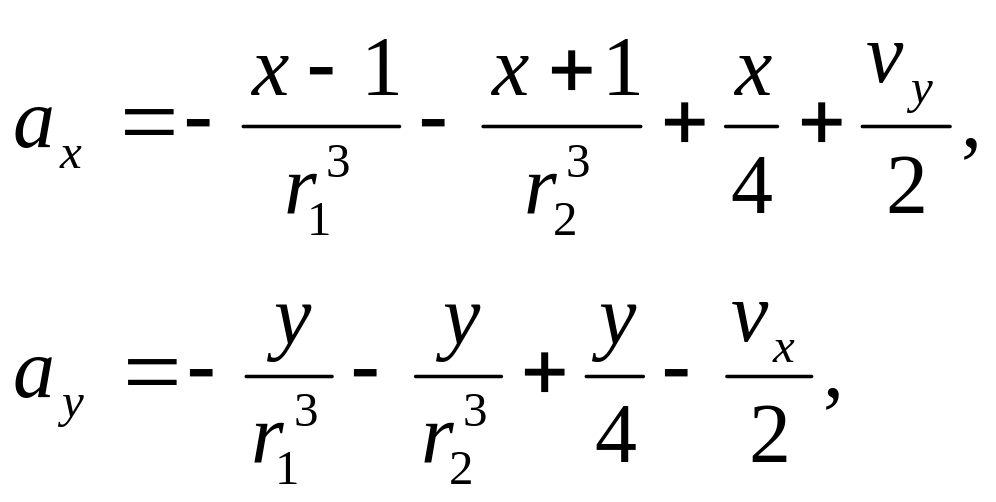(13.24)

где

Запишем выражение для потенциальной энергии планеты:

, (13.25)

где последнее слагаемое соответствует центробежной силе. Явное выражение через координаты имеет довольно громоздкий вид:

. (13.26)

На рис.13.4 показана потенциальная поверхность, описываемая функцией (13.26), и ее сечение, проходящее через ось .

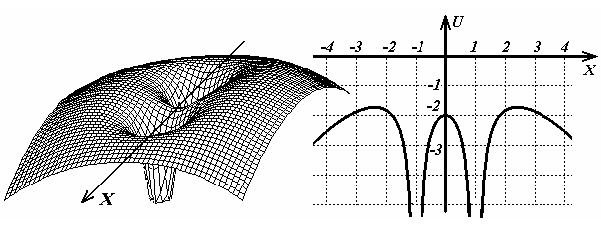
Рис. 13.4

Мало того, что трудно себе вообразить движение шарика по этой поверхности с перескоками из одной ямы в другую, но даже если это и представить, то движение планеты будет иным. В уравнения движения входит сила Кориолиса, которая зависит от скорости. Так как эта сила перпендикулярна скорости, то она работы не совершает, поэтому полная механическая энергия системы будет сохраняться. Однако, из-за наличия сил, зависящих от скорости, движение планеты будет заметно отличаться от движения шарика по нарисованной поверхности⁸. Тем не менее, условие сохранения механической энергии следует использовать для контроля точности компьютерных расчетов.

Заметим, что момент импульса планеты сохраняться не будет - сила Кориолиса не является центральной, поэтому ее действие приводит к изменению момента импульса планеты.

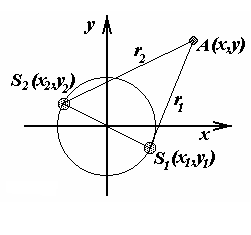
Рис. 13.5

Второй подход к решению задачи⁹ заключается в описании движения планеты в «обычной» инерциальной системе отсчета, в которой явным образом учитывается движение самих звезд. Такая декартовая система отсчета показана на рис.13.5. Сохраняя прежнюю систему единиц, будем считать, что звезды движутся по окружности единичного радиуса, центр которой совпадает с началом отсчета. Чтобы такое движение было возможно, звезды должны находиться в противофазе, иными словами в любой момент времени соответствующие координаты звезд противоположны по знаку. Следовательно, зависимость координат звезд от времени можно описать формулами¹⁰:

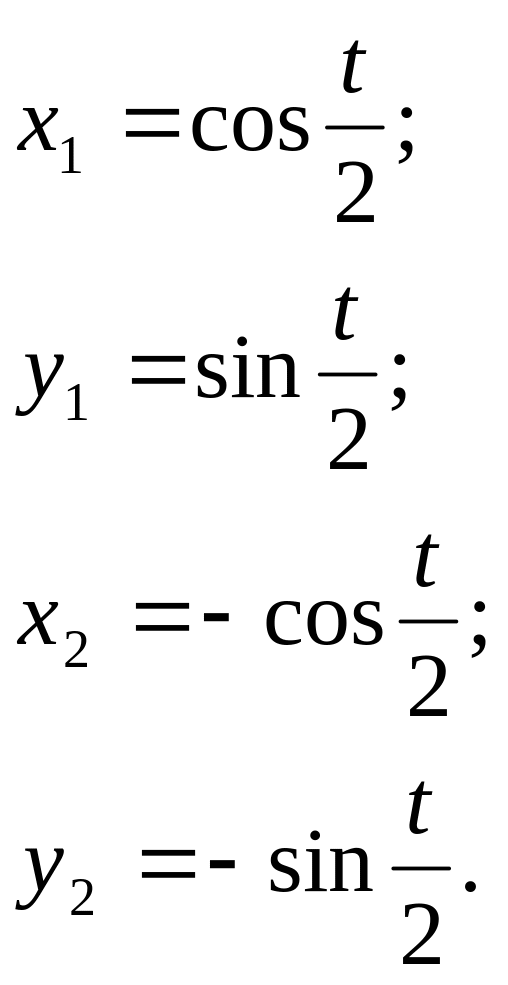(13.27)

В уравнениях движения планеты необходимо корректно записать выражения для сил притяжения к обеим звездам. На этом ограничим свои комментарии и приведем систему уравнений:

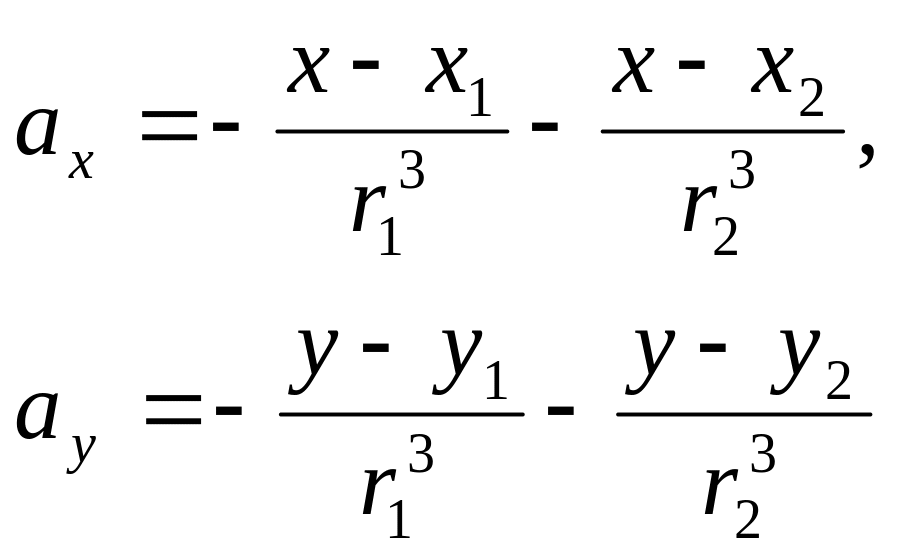(13.27)

где

К данной системе (13.26)-(13.27) необходимо добавить начальные условия - четыре числа: начальные координаты и проекции начальной скорости на оси координат.

Сравним системы уравнений одного и того же движения: в инерциальной системе (13.26)-(13.27) и неинерциальной, вращающейся системе отсчета (13.20). Уравнения движения в инерциальной системе отсчета более понятны - в них фигурируют только силы гравитационного притяжения, однако (и это существенный недостаток), в эти уравнения явным образом входит время. Поэтому механическая энергия и момент импульса планеты сохраняться не будут! Конечно, полная энергия и полный момент импульса системы (две звезды - одна планета) должны сохранятся. Но мы заранее задали закон движения звезд - то есть пренебрегли влиянием движения планеты на движение звезд. Это приближение вполне применимо, если масса звезд значительно превышает массу планеты¹¹. Уравнения движения в неинерциальной системе отсчета таковы, что механическая энергия планеты сохраняется. Никакого противоречия между этими системами нет - речь идет о действительно разных энергиях, подумайте, кинетическая энергия зависит от выбора системы отсчета и достаточно сложным образом. Отметим также что, момент импульса планеты не будет сохраняться потому, что гравитационные силы направлены не к началу отсчета, поэтому момент этих сил отличен от нуля, следовательно, их действие приводит к изменению момента импульса. Попытка наглядно вообразить себе движение планеты может быть предпринята в следующей форме: представьте, что потенциальная поверхность, похожая на изображенную рис. 13.4, вращается вокруг вертикальной оси, и по этой вращающейся поверхности движется шарик. Представили? Нам не удается!

Итак, подведем итог: уравнения движения в инерциальной системе отсчета понятнее, но значительно сложнее для решения и анализа. Вот и выбирайте, что предпочтительнее: один раз разобраться с силой Кориолиса, или всю жизнь мучаться с уравнениями, содержащими время в явном виде? Мы же поступим дипломатично - решим обе системы уравнений, как в инерциальной системе отсчета, так и в неинерциальной. Сравнение этих решений позволит нам (конечно, при условии их совпадения) получить подтверждение их правильности.

Для сравнения решений нам необходимо уметь переходить из одной системы отсчета в другую. Получим формулы перехода от координат неинерциальной системы отсчета к координатам инерциальной системы и обратно.

Начала отсчета этих систем отсчета совпадают (рис.13.6), обозначим угол между соответствующими осями координат , который зависит от времени по закону .

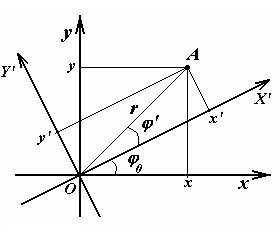
Рис. 13.6

Формулы перехода можно получить различными способами, мы же воспользуемся полярными координатами: - расстояние до начала координат одинаково в обеих системах отсчета; если радиус-вектор , образует угол с осью , то угол между радиус-вектором и осью будет равен .

Декартовые координаты точки в неинерциальной системе отсчета выражаются знакомыми формулами:

, (13.28)

аналогичные соотношения можно записать и для координат инерциальной системы отсчета:

.

Используя тригонометрические формулы для синуса и косинуса и выражения (13.28), получим искомые соотношения между координатами:

. (13.29)

Для того чтобы получить обратные преобразования, заметим, что полученные формулы фактически описывают поворот осей координат на угол по часовой стрелки, а обратный переход есть поворот осей на тот же угол против часовой стрелки. Поэтому в полученных выражениях достаточно заменить угол на противоположный . Следовательно, формулы обратного преобразования имеют вид:

. (13.30)

Обращаем ваше внимание, на необходимость согласования и начальных условий в различных системах отсчета - особенно внимательно следите за выражением для скоростей. В начальный момент времени угол между осями координат , то есть, они совпадают, поэтому начальные значения координат в обеих системах координат оказываются равными.

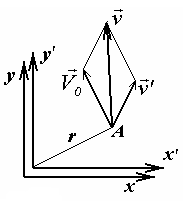
Рис. 13.7

Чтобы найти формулы преобразования скоростей при переходе из одной системы отсчета в другую необходимо учесть, так называемую, переносную скорость движения неинерциальной системы относительно инерциальной (рис.13.7). Так, если планета находится на расстоянии от начала отсчета, то переносная скорость в этой точке будет равна и направлена перпендикулярно к радиус-вектору точки . Поэтому скорость планеты в инерциальной системе отсчета будет определяться выражением:

, (13.31)

где - скорость планеты относительно вращающейся неинерциальной системы отсчета. Как видно, формулы преобразования скоростей сложны, зависят от координат точки. Поэтому чтобы несколько «упростить себе жизнь», будем задавать «специфические» начальные условия: будем считать, что при планета находится на оси и ее скорость направлена перпендикулярно этой оси (рис.13.8).

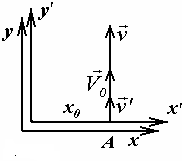
Рис. 13.8

В этом случае векторы всех скоростей направлены вдоль одной оси, поэтому переход от одной системы отсчета в другую упрощается:

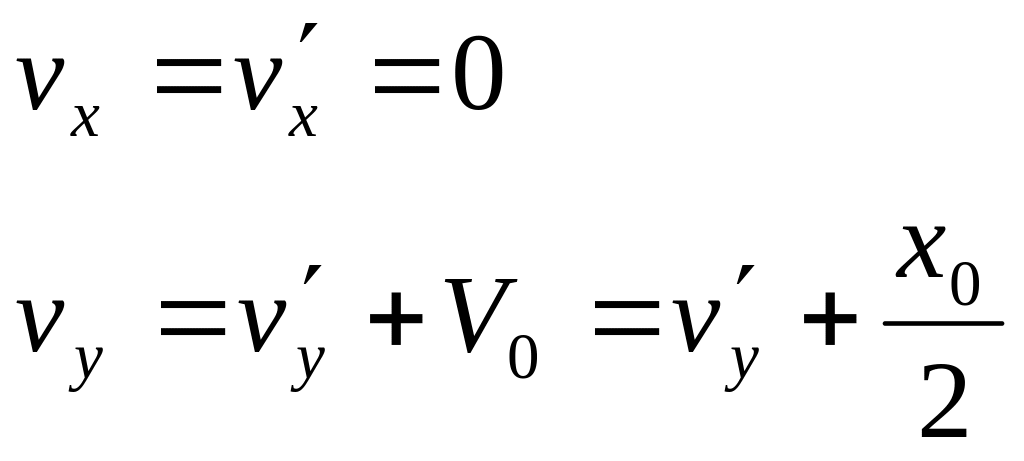. (13.32)

В принципе, получить общие формулы преобразования скоростей не так уже сложно, достаточно продифференцировать формулы преобразования координат (13.29) или (13.30). Так, например, вычисляя производную от первой формулы (13.29), получаем:

.

При вычислениях учтено, что производная от угла поворота есть угловая скорость .

Вот теперь можно уверенно сказать: - «Описывайте движение в той системе, где вам больше нравится, а затем переходите в ту, которая требуется».

Задачу будем решать численно известным методом Эйлера. Как всегда, основная проблема - выбор разумного значения шага изменения времени . Методы решения этой проблемы, в принципе остаются прежними - оценка характерного времени системы¹², уменьшение его на 3-4 порядка, а затем экспериментально подбираем значение шага, достаточного для достижения требуемой точности.

В данной задаче проблема выбора осложнена еще одним часто встречающимся обстоятельством - ускорение планеты может изменятся в широких пределах, особенно резко возрастая при приближении к одной из звезд. Поэтому при малом расстоянии до звезды шаг должен быть очень малым. Если же выбрать таким малым, то при больших расстояниях время расчета неоправданно возрастает. Выход из этой ситуации почти очевиден - шаг изменения времени нужно сделать переменным, зависящим от величины ускорения. Проще всего, положить величину обратно пропорциональной полному ускорению планеты - в этом случае величина изменения скорости будет оставаться примерно постоянной. Таким образом, имеет смысл добавить еще одну «строчку»: после вычисления проекций ускорения пересчитать значение шага :

, (13.32)

где величина - некоторая постоянная, достойная подбора по изложенной методике¹³.

Численный метод, который мы применяем для решения уравнений движения, является приближенным, поэтому обязательно необходимо предусмотреть в программе постоянный контроль точности решения. В данной задаче такой контроль можно вести, рассчитывая значение полной механической энергии. Причем лучше использовать выражение для энергии, содержащее значение угловой скорости (это автоматически контролирует и точность расчета угла поворота), то есть пользоваться формулой:

.

При анализе колебаний (модель 11) в качестве критерия использовалось значение относительного изменения энергии. В данной задаче такой подход несколько неудобен, так как полная энергия может равняться нулю. Максимальное по модулю значение энергии для замкнутых орбит равно 1 (если положить , то полная энергия равна -1), поэтому в качестве критерия точности можно использовать модуль разности рассчитанного и начального значений энергии, то есть величину . Если эта величина превышает некоторый указанный предел¹⁴, то решение следует прекратить. В дальнейших примерах величину будем считать равной . Этот способ контроля мы применим в задаче c одной звездой.

Каким способом будем проводить контроль точности решения в задаче с двумя звездами? При решении системы уравнений движения (13.24) следует контролировать постоянство механической энергии планеты, которая рассчитывается по формуле:

. (13.33)

При описании движения планеты в инерциальной системе отсчета полная механическая энергия планеты не сохраняется. Поэтому контроль точности по условию сохранения энергии невозможен. Однако, «энергетический контроль» возможен (и необходим) в несколько иной форме - с помощью известной из курса механики теоремы о кинетической энергии: «изменение кинетической энергии системы равно работе внешних сил». На языке численных расчетов эта теорема выражается уравнением¹⁵:

, (13.34)

где - работа внешних сил, которую можно последовательно рассчитывать в ходе решения системы. Так как работа на небольшом участке перемещения определяется скалярным произведением , то на каждом шаге она рассчитывается по формуле:

. (13.35)

Таким способом можно постоянно подсчитывать работу внешних сил, и тем самым контролировать выполнение условия (13.34). Очевидно, что, из-за неизбежных погрешностей расчетов, не следует ожидать абсолютно точного соблюдения этого равенства, поэтому можно ограничиться разумной точностью. Так нам показалось достаточным выполнение этого равенства с погрешностью не превышающей 5%.

Итак, мы имеем три способа¹⁶ проверки корректности расчетов траекторий:

- сравнение результатов, полученных при различных значениях шага ;

- «энергетический» контроль;

- решение в двух системах отсчета, неинерциальной и инерциальной, с последующим переходом в одну из них.

Может показаться, что тройной контроль немного избыточен, однако сложность поставленной задачи его оправдывает.

Модель 13. Выход в космос

1. Постановка задачи. Исследовать возможные орбиты движения планеты в системах “Планета-звезда” и “Планета – двойная звезда”. Влиянием других звезд и планет на движение рассматриваемой системы пренебречь. Звезда и планета взаимодействуют с силой, подчиняющейся закону всемирного тяготения Ньютона.

2. Математическая модель.

Одна звезда.

Уравнение движения планеты.

Угловая скорость.

Начальные условия.

Две звезды

а) неинерциальная система отсчета.

Уравнение движения планеты.

где

Начальные условия.

б) инерциальная система отсчета.

Уравнение движения планеты.

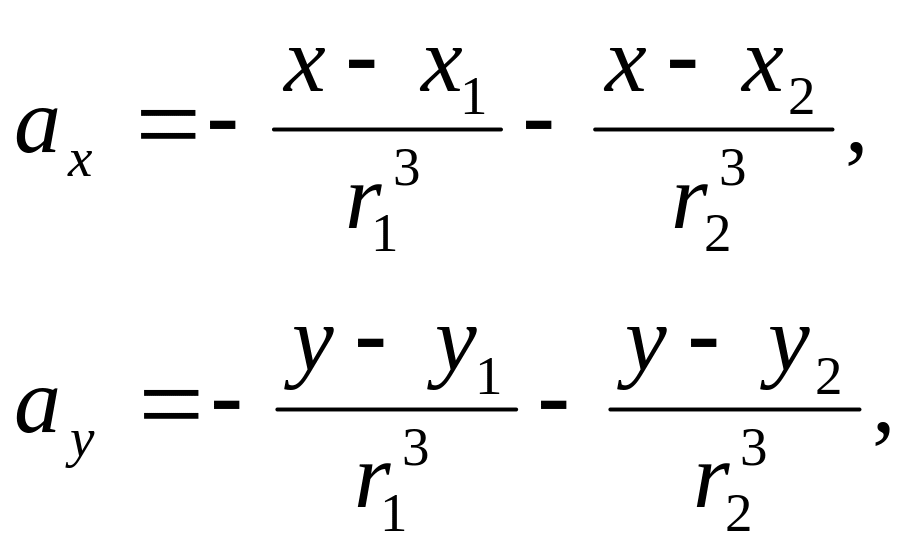
Закон движения звезд.

где ;

- координаты планеты;

- координаты первой и второй звезд.

Начальные условия.