4. Базис скінчено вимірного векторного простору. Координати векторів.

Означення 12. Базисом -вимірного векторного простору називається довільна впорядкована лінійно незалежна система із векторів цього простору.

Зауваження 1. З означення випливає, що у векторному просторі існує безліч базисів.

Зауваження 2. Базис називають ще впорядкованою максимально лінійно незалежною системою векторів у просторі. Слово «максимально» тут означає, що до системи базисних векторів неможливо приєднати жодного вектору простору так, щоб система залишалась лінійно незалежною.

Теорема. Кожний вектор -вимірного векторного простору може бути поданий у вигляді лінійної комбінації векторів базису, причому таке подання єдине.

Доведення. Нехай – деякий базис векторного простору . Нехай . Тоді система векторів є лінійно залежною, тобто існує нетривіальна лінійна комбінація: . В цій лінійній комбінації коефіцієнт , інакше і тоді система векторів – лінійно залежна, що суперечить умові. Отже, маємо: , тобто вектор є лінійною комбінацією базисних векторів. Покажемо, що таке подання єдине. Від супротивного припустимо, що існує два різних розклади вектора по системі базисних векторів: та . Звідси випливає, що , а оскільки вектори лінійно незалежні, то .

Означення 13. Якщо – базис векторного простору і – розклад деякого вектору по базису , то коефіцієнти цього розкладу називаються координатами вектора в базисі .

З доведеної вище теореми випливає, що будь-який вектор простору однозначно визначається своїм набором координат у вибраному базисі. Це дозволяє повністю абстрагуватись від самої природи векторного простору і мати справу лише з наборами координат замість векторів. Крім того, це вказує на певну «схожість» всіх векторних просторів однакової розмірності. Пізніше ми доведемо теорему, в якій ця схожість називатиметься ізоморфізмом векторних просторів.

Зауваження. Координати вектора будемо записувати як вектор-стовпчик, позначаючи їх наступним чином: .

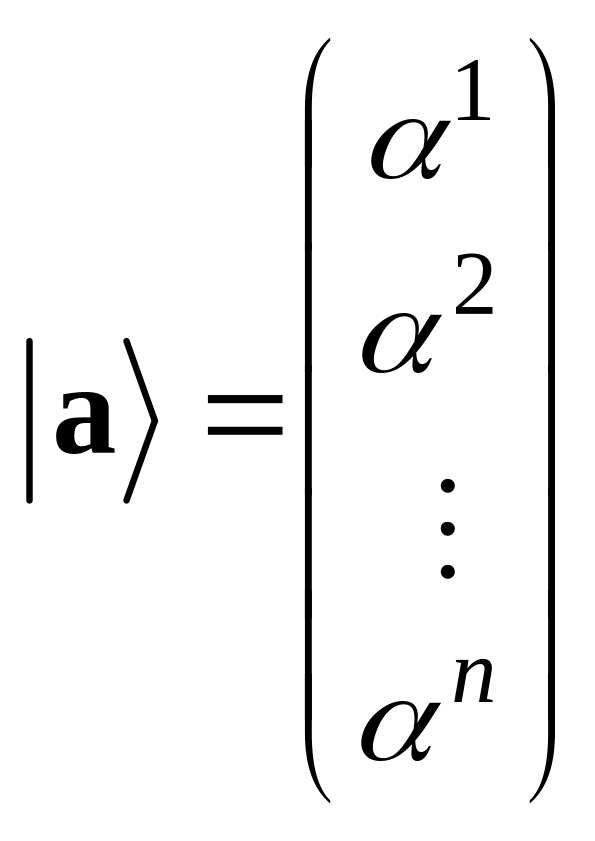Наслідки з теореми.

1. Координати будь-якого вектору простору у фіксованому базисі визначаються однозначно.

2. Два вектори рівні тоді і тільки тоді, коли рівні їх координати у фіксованому базисі.

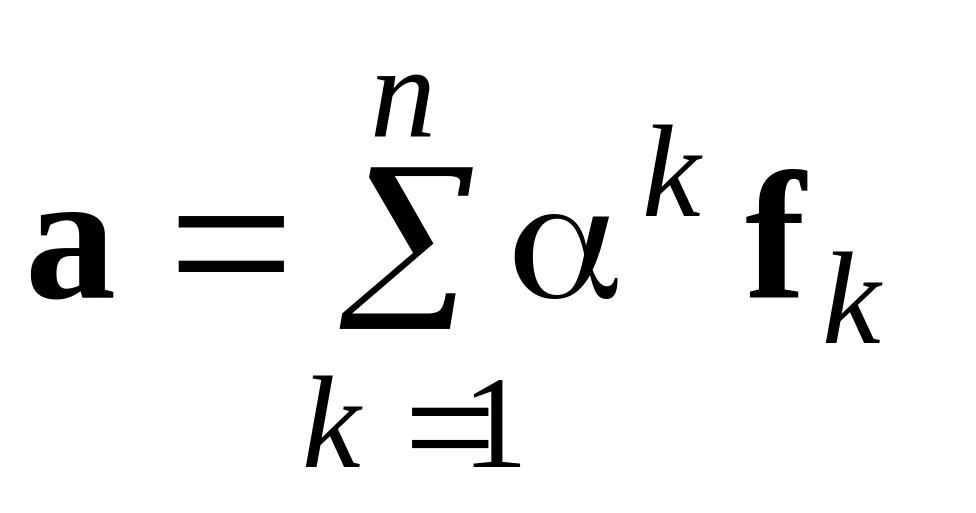3. Якщо та 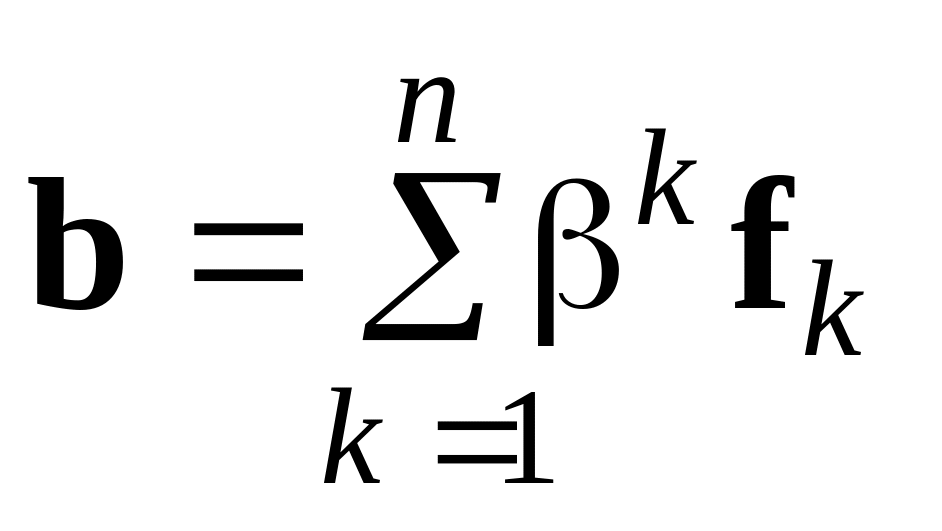розклади довільних векторів простру по базису , то вектор 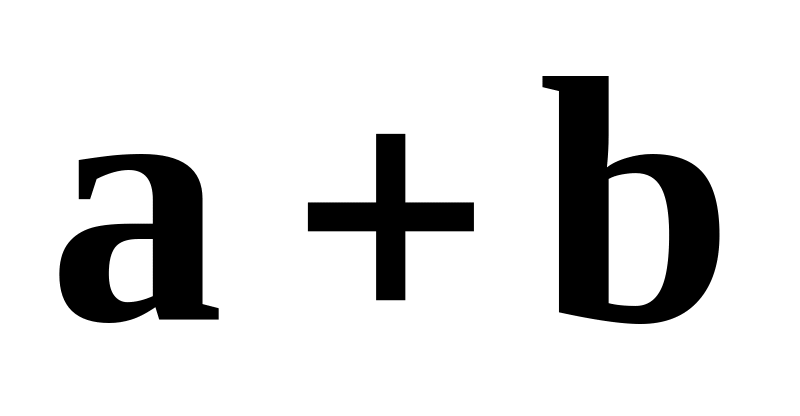в цьому базисі матиме координати 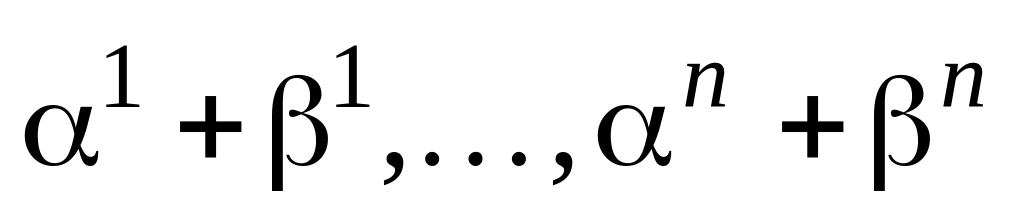, а вектор – координати

. Доведіть цей факт самостійно.

4. Система векторів простору лінійно незалежна тоді і тільки тоді, коли лінійно незалежна система вектор-стовпчиків їх координат. Доведіть це самостійно.

5. Системи координат в просторі геометричних векторів.

Повернемось у тривимірний простір геометричних векторів. Очевидно, базис в ньому утворюють довільні три не компланарні вектори (нагадаємо, що компланарними називаються три вектори, які паралельні одній площині). Отже, виберемо три не компланарних вектори та зведемо їх до спільного початку – деякої точки О. Одержимо загальну афінну систему координат. Якщо три базисних вектори взаємно перпендикулярні, система координат називається прямокутною. І нарешті, якщо у прямокутній системі координат базисні вектори мають одиничну довжину, маємо знайому із школи ПДСК – прямокутну декартову систему координат. Базисні вектори в ній позначаються, як вже згадувалось вище, , а координати вектора називаються відповідно абсциса, ордината та апліката. Будемо позначати їх наступним чином: .

Якщо розглядаються лише вектори, що належать одній площині, то крім ПДСК на площині використовують також полярну систему координат. Вважатимемо, що цей матеріал добре засвоєний у курсі математичного аналізу.

Приклад. Точки K та L – середини сторін AB та BC паралелограма OABC. Довести, що точка перетину діагоналей паралелограму співпадає з точкою перетину медіан трикутника OKL.

Ведемо афінну систему координат на площині: точка О – початок, та – базисні вектори.

П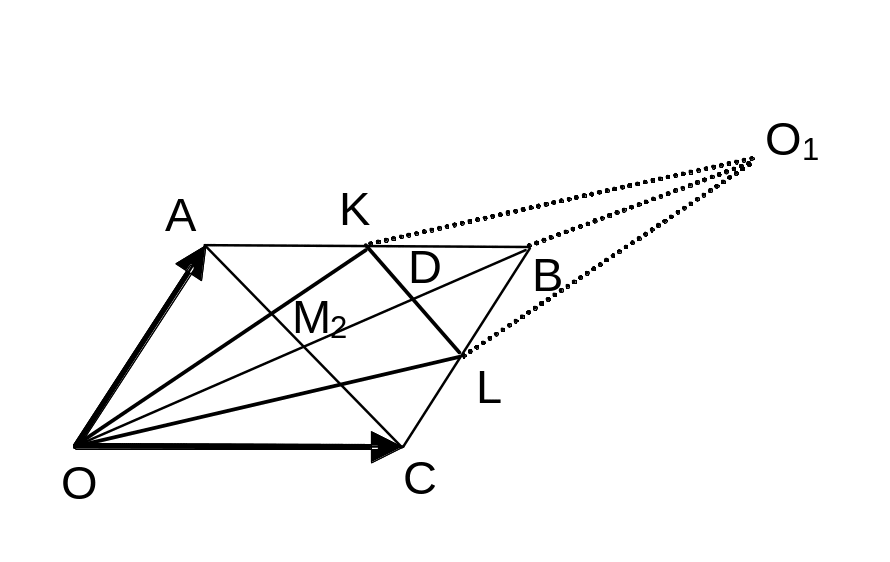 означимо М₁ – точку перетину діагоналей паралелограма OABC. Тоді за правилами додавання векторів маємо , тому . Тепер розглянемо трикутник OKL. Позначимо М₂ – точку перетину медіан цього трикутника (див. мал.). Маємо , . Для паралелограма OKО₁L діагональ OО₁ визначається як сума сторін-векторів: . Тоді медіана OD трикутника OKL – це половина даної діагоналі: . Як відомо медіани трикутника в точці перетину діляться у співвідношенні 2:1, тому для точки їх перетину справедлива рівність: , що означає векторну рівність , тому точки М₁ та М₂ співпадають.

4