4.2. Моделювання одномірних часових рядів

Результатом виявлення основної тенденції є висновок про те, що існує можливість поширити закономірності розвитку об'єкта в минулому на його майбутнє, тобто провести операцію екстраполяції. Екстраполяційні методи засновані на припущенні про те, що закон зміни, який мав місце в минулому для процесу, який досліджується, збережеться для нього і у майбутньому, тобто на факті наявності у розвитку явища основної тенденції. При дотриманні цих вимог екстраполяція здійснюється шляхом підстановки у знайдене рівняння тренда (модель ) значення незалежної змінної , що відповідає величині періоду упередження (прогнозу).

Методика екстраполяції здійснюється за таким алгоритмом:

1. Упорядкування минулих даних.

2. Згладжування ЧР.

3. Виділення тренда.

4. Визначення рівняння тренда.

5. Розрахунок прогнозного значення.

6. Оцінка довірчого інтервалу із заданою ймовірністю.

Нижче буде розглянуто методики проведення згладжування початкових даних для прогнозування – початкового ЧР та принципів визначення рівняння тренда.

4.2.1. Методи згладжування часових рядів

Згладжування часових рядів за допомогою ковзної середньої

Одним з найбільш широко відомих методів згладжування ЧР є метод ковзної середньої (МКС). Застосовуючи цей метод, можна вилучити випадкові коливання й одержати значення, які відповідають впливу головних факторів. Згладжування за допомогою ковзних середніх побудоване на тому, що в середніх величинах взаємно погашаються випадкові відхилення. Це відбувається внаслідок того, що початкові рівні ЧР замінюються середньою арифметичною величиною усередині обраного періоду часу – інтервалу згладжування . Отримане значення відноситься до середини обраного періоду. Потім період зрушується на одне спостереження й розрахунок середньої повторюється, причому періоди визначення середньої беруться увесь час однаковими. Таким чином, у кожному випадку середня центрована, тобто віднесена до серединної точки інтервалу згладжування і являє собою рівень для цієї точки. При застосуванні МКС в розрахунках беруть участь всі рівні ряду. Чим ширшим є інтервал згладжування, тим більш плавним стає тренд. Згладжений ряд коротше початкового на спостережень ( = - величина інтервалу згладжування). При великих значеннях коливальність згладженого ряду значно знижується. Одночасно помітно скорочується кількість спостережень, що створює труднощі.

З вибором інтервалу згладжування пов'язане питання про кількість рівнів ряду, які беруть участь у розрахунку, і техніку цього розрахунку. Якщо число членів інтервалу згладжування непарне, то отримані за МКС значення ряду приходяться на середній член інтервалу ковзання. При парній кількості рівнів отримані значення не можна віднести до жодного рівню ряду – вони будуть розташовуватися в проміжках між рівнями.

Для першого випадку ковзна середня буде обчислюватися за формулою

. (4.2)

Для другого випадку ковзна середня визначається наступним чином:

. (4.3)

Для формул (4.2) і (4.3): - величина -ї ковзної середньої; - -й рівень часового ряду ; - задане ціле позитивне число, за допомогою якого визначається величина інтервалу згладжування;

- число рівнів часового ряду; - змінний індекс для інтервалу згладжування .

Метод експоненціального згладжування(МЕЗ)

Особливість його полягає у тому, що в процедурі вирівнювання кожного спостереження використовуються тільки значення попередніх рівнів ЧР, взятих з певною вагою. Вага кожного спостереження зменшується за мірою його віддалення від моменту, для якого визначається згладжене значення. Згладжене значення рівня ряду на момент визначається за формулою

, (4.4)

де - значення рівня ЧР, який підлягає експоненціальному згладжуванню в момент ; - значення рівня ЧР для моменту , який був попередньо згладжений експоненціально; - значення рівня незгладженого ЧР в момент ; — вага -го значення ряду динаміки (або параметр згладжування ).

З формули (4.4) видно, що при обчисленні експоненціальної середньої використовується лише попередня експоненціальна середня й останнє спостереження , а всі попередні рівні ряду “забуваються”.

При практичному використанні МЕЗ виникають деякі труднощі. Основними з них є вибір значення параметра згладжування і визначення початкової умови . Від чисельного значення параметра залежить, наскільки швидко буде зменшуватися вага попередніх спостережень і, відповідно до цього, ступінь їхнього впливу на рівень, який згладжується. Чим більше значення параметра , тим менше позначається вплив попередніх рівнів і відповідно меншим виявляється згладжувальний вплив експоненціальної середньої. Пошук компромісного значення параметра згладжування складає задачу оптимізації моделі, яка й дотепер до кінця ще не вирішена.

Автор методу експоненціального згладжування англійський учений Р.Г.Браун запропонував наступну формулу розрахунку :

, (4.5)

де - число рівнів, які входять в інтервал згладжування. Величина , отже, і визначаються в цьому випадку емпірично. Як практичний компроміс автор рекомендує обирати у межах від 0,1 до 0,3.

Задачу вибору параметра , який визначає початкові умови згладжування, пропонується вирішувати наступним чином: якщо є дані про розвиток явища в минулому, то в якості можна використати середню арифметичну всіх наявних рівнів ЧР або якоїсь їхньої частини, тобто . Якщо ж таких відомостей немає, то в якості використовують вихідне (перше) значення рівня ЧР. Вага, яка приписана цьому рівню, швидко зменшується в міру віддалення від першого рівня ряду, разом із цим швидко зменшується його вплив на значення обчислених експоненціальних середніх.

4.2.2. Описання рівняння тренду за допомогою методу найменших квадратів

Метод спрямований на визначення найкращої (з точки зору найменшої статистичної похибки) форми кривої , яка апроксимує точки розкиду експериментальних даних згладженого ЧР. Існують різні прийоми, що дозволяють вибрати форму кривої, яка досить добре апроксимує ЧР. Найбільш простий шлях - це візуальний, на основі побудованого графічного зображення ЧР. За видом такого емпіричного графіка підбирається такий вид рівняння кривої, яка ближче за все підходить до емпіричних точок розкиду. Апроксимація може бути здійснена за рахунок використання:

1) поліномів

• першого ступеню: 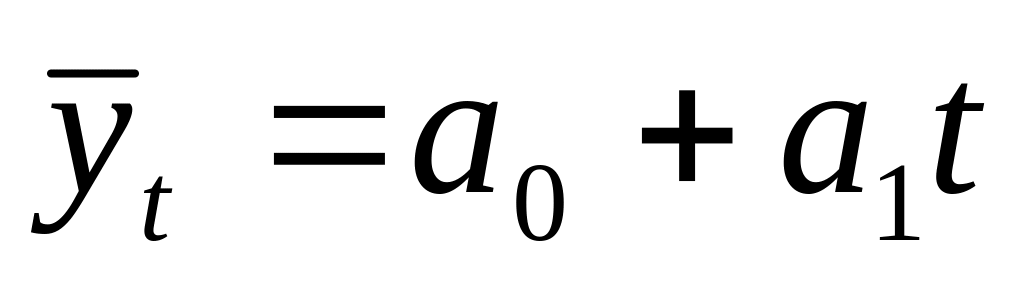; (4.6)

• другого ступеню: ; (4.7)

• третього ступеню: ; (4.8)

• -го ступеню: ; (4.9)

2) експонент

; (4.10)

; (4.11)

; (4.12)

3) логістичних кривих

, (4.13)

де - основа натурального логарифма;

, (4.14)

4) кривих Гомперца: (4.15)

або функцій інших видів.

Параметри та наведених вище функцій мають певний якісний зміст і досить легко інтерпретуються.

Так, наприклад, рівняння прямої (поліному першого ступеню) характеризує постійний приріст значень параметра прогнозування , рівний одиницям, при початковому рівні .

У рівнянні параболи (поліному другого степеню) коефіцієнт виражає початкову швидкість росту, а коефіцієнт - постійну швидкість зміни приросту. Якщо рівень явища зростає із прискоренням, то величина цього прискорення в середньому за період дослідження дорівнює одиницям.

Експонента відбиває постійний відносний ріст, рівний одиницям, а експонента характеризує постійний відносний приріст, рівний одиницям.

На даний час у науковій літературі дано опис декількох десятків математичних функцій (кривих росту), з них найчастіше використовуються в прогнозуванні поліноміальні, експоненціальні й -подібні криві.

Практика аналітичного моделювання свідчить про те, що існує закономірність між характером розвитку процесу, який підлягає прогнозуванню, та вибором виду функції, яка повинна описувати ці явища. Так, монотонне зростання або спадання значень показника процесу характеризують функції: лінійна, параболічна, степенева, проста експоненціальна крива, модифікована експонента або гіперболічна крива.

Для моделювання ЧР, у яких проявляється швидкий розвиток процесу на його початку і згасання у закінченні (процеси насичення) застосовуються логістичні криві.

Процеси, які характеризуються наявністю екстремальних значень показника , описується кривою Гомперца.

Оцінки у формулах (4.6)-(4.9) знаходяться за методом найменших квадратів, суть якого полягає у відшуканні таких параметрів функції у залежності , при яких сума квадратів відхилень розрахункових значень рівнів, обчислених за цією формулою, від їхніх фактичних значень була б мінімальною.

Вибір виду функції, що описує тренд, параметри якої визначаються методом найменших квадратів, здійснюється в більшості випадків емпірично, шляхом побудови ряду функцій і порівняння їх між собою за величиною середньоквадратичної помилки, яка обчислюється за формулою

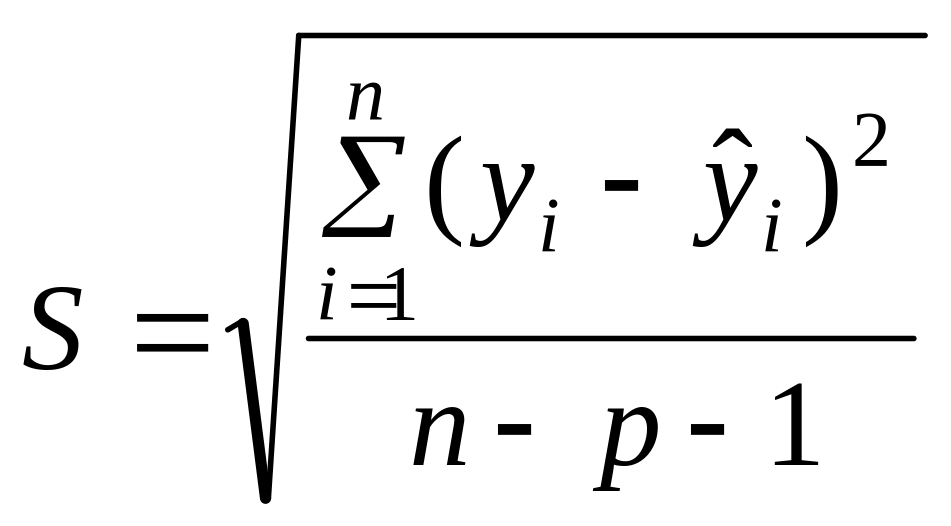(4.16)

де - розрахункові значення рівнів ЧР; - фактичні рівні ЧР; - число рівнів у ЧР; - число параметрів а_і, які знаходяться у формулах, що описують тренд.