3. Деревья бинарного поиска

На практике в большинстве таблиц встречаются элементы, к которым обращаются чаще, чем к другим. Такие элементы будут быстрее обнаружены, если находятся в «средних точках» на ранних этапах работы бинарного поиска. Обеспечить такое их расположение невозможно для последовательно распределенных таблиц, элементы которых упорядочены. Для этого введем особую структуру данных.

Дерево бинарного поиска над множеством T={x₁, …, x_n} – бинарное дерево, узлы которого содержат элементы множества Т так, что при симметричном обходе дерева порядок узлов совпадает с порядком их во множестве Т.

Пример 1: Два дерева двоичного поиска над таблицей Т={5, 7, 10, 12, 14, 15, 18}

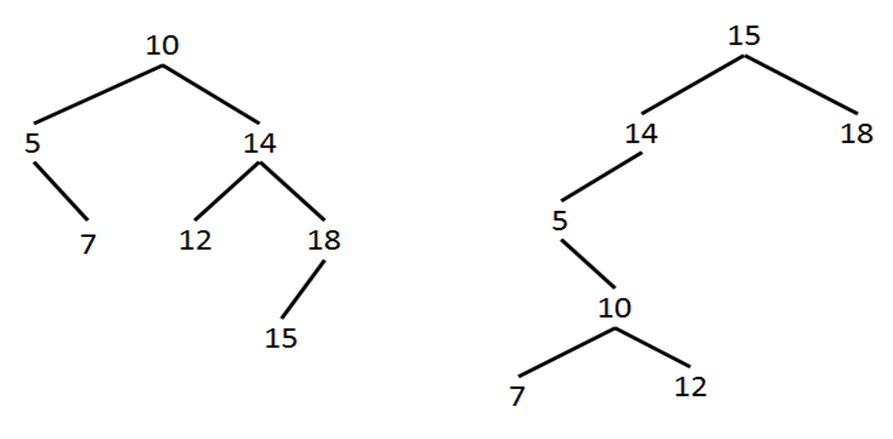
Характеристическим свойством дерева двоичного поиска является то, что все элементы, хранящиеся в узлах левого поддерева любого узла х меньше элемента, находящегося в х, а все элементы в узлах правого поддерева узла х больше, чем элементы в узле х.

Для поиска элемента х в дереве бинарного поиска, х сравнивается с элементом, стоящим в корне.

1. Если корня нет(дерево пусто), то х не найден.

2. Если х совпадает с элементом в корне, то х найден.

3. Если х меньше элемента в корне, то продолжить поиск в левом поддереве.

4. Если х больше элемента в корне, продолжить поиск в правом поддереве.

Рассмотрим далее функцию MEMBER(x, A), которая осуществляет поиск элемента х в бинарном дереве А. Здесь все элементы множества имеют тип elementtype(это может быть встроенный в язык программирования или определенный пользователем).

Узлы дерева имеют тип nodetype, т.е. запись, содержащее поле element для элементов множества и два поля leftchild и rigthchild для указателей на левого и правого сына.

type

nodetype=record

element:elementtype;

leftchild, rigthchild:^nodetype;

end;

Для дерева определим тип SET-указатель на корень дерева двоичного поиска:

type SET:^nodetype;

function MEMBER ( х: elementtype; A: SET ): boolean;

{ возвращает true, если элемент х принадлежит множеству А, false — в противном случае }

begin

if A = nil then

return(false) { x не может принадлежать Ø }

else if x = A^.element then

return (true)

else if x < A^.element then

return (MEMBER(x, A^.leftchild))

else { x > A^.element }

return(MEMBER(x, A^.rightchild))

end; { MEMBER }

Для работы с бинарными деревьями поиска также требуются процедуры INSERT(x, A) и DELETE(x, A), которые добавляют и удаляют элемент из бинарного дерева соответственно.

§13 Абстрактные типы данных. Методы представления множеств.

Абстрактный тип данных (АТД) можно определить как математическую модель объекта с совокупностью операторов, определенных над объектом в рамках этой модели.

Простым примером абстрактного типа данных могут служить множества целых чисел с операторами объединения, пересечения и разности множеств.

Реализация АТД подразумевает 1) определение с помощью выбранного языка программирования переменных, представляющих объекты этого АТД; 2) написание процедуры для каждого оператора, выполняемого над объектами АТД.

Реализация АТД зависит от структуры данных, представляющих АТД. Каждая структура данных строится на основе базовых типов данных применяемого языка программирования, используя доступные в этом языке средства структурирования данных. Например, структуры массивов и записей — два важных средства структурирования данных, возможных в языке Pascal.

Часто в рамках одной математической модели определяются и реализуются различные АТД. Причина в том, что над объектами этих АТД необходимо выполнять различные действия, т.е. определять операторы разных видов.

Особенности реализации АТД «Множество».

Рассмотрим операторы, выполняемые над множествами, которые часто включаются в реализацию различных абстрактных типов данных. Некоторые из этих операторов имеют общепринятые (на сегодняшний день) названия и эффективные методы их реализации.

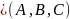1. — оператор объединения. Имеет "входными" аргументами множества 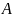и 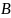, а в качестве результата — "выходное" множество , равное .

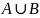2. ‑ оператор пересечения. Имеет "входными" аргументами множества и , а в качестве результата — "выходное" множество , равное .

3. ‑ оператор вычитания. Имеет "входными" аргументами множества и , а в качестве результата — "выходное" множество , равное .

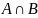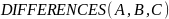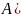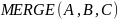4. ‑ оператор слияния. Используется очень редко. Имеет "входными" аргументами множества и , а в качестве результата — "выходное" множество , равное , но результат будет не определен, если 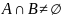. Это единственное отличие оператора от оператора . Функциональности оператора , при написании программы вполне достаточно.

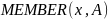5. – оператор проверки принадлежности элемента множеству. Имеет входящие аргументы множество и объект 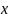того же типа, что и элементы множества , и возвращает булево значение 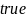(истина), если 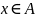, и значение 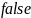(ложь), если .

6. ‑ оператор присваивает множеству значение пустого множества.

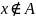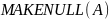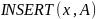7. – оператор вставки элемента в множество. Имеет аргументами объект , который имеет тот же тип данных, что и элементы множества . Данный оператор делает элементом множества . Другими словами, новым значением множества будет множество 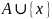. В случае, когда элемент уже присутствует в множестве , это множество не изменяется в результате выполнения данной процедуры.

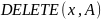8. ‑ оператор удаления. Удаляет элемент из множества , т.е. заменяет множество множеством 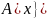. Если элемента нет в множестве , то это множество не изменяется.

9. ‑ оператор присваивания. Присваивает множеству в качестве значения множество . На практике, обычно, происходит копирование множества во множество . Такой алгоритм связан с особенностями реализации языков программирования.

10. ‑ оператор поиска минимального элемента. Возвращает наименьший элемент множества . Для применения этой функции необходимо, чтобы элементы множества А были линейно упорядочены.

11. ‑ оператор поиска максимального элемента. Возвращает наибольший элемент множества . Реализация аналогично оператору .

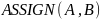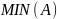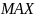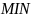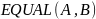12. ‑ оператор равенства множеств. Возвращает значение тогда и только тогда, когда множества и состоят из одних и тех же элементов, в противном случае возвращает значение .

Далее будет предполагаться, что все рассматриваемые множества упорядочены по возрастанию. На данном условии будут строиться все алгоритмы работы операторов.