Метод хорд.
Метод хорд является более быстрым способом нахождения корня уравнения f(x0)=0 лежащем на отрезке [a,b], в током, что f(a)*f(b)<0. Требуется найти корень с погрешностью e. Для определенности пусть f(a)<0,f(b)>0. Делится отрезок в отношении - f(a)/f(b). Это дает приближенное значение корня x, равное x=a+h, где
x=a+ -(f(a))*(b-a)/-(f(a)+f(b); h= -(f(a))*(b-a)/-(f(a)+f(b);
Далее применяя этот прием к тому из отрезков [a,x] или [x,b] на концах, которого функция имеет противоположные знаки, получим второе приближение корня.
Геометрический метод хорд эквивалентен замене кривой y=f(x), хордой проходящей через точки (a и b) уравнения хорды:
(x-a)/(b-a)=(y-f(a))/(f(b)-f(a)), полагая, что x=x1 y=0, получим
x1=a – f(a)*(b-a)/(f(b)-f(a)), где x1-первое приближение корня. Для сходимости процесса корень должен быть отделен и вторая производная должна сохранять знак на [a,b].
Рабочие формулы метода хорд:
а) для случая f(a)<0
xn+1= xn- f(xn)*(b-xn)/f(b)-f(xn)
б) для случая f(a)>0
xn+1= xn- f(xn)*(xn-a)/f(xn)-f(a)
Метод простой итерации.
Суть метода состоит в замене уравнения f(x) на уравнение x=φ(x). Процесс нахождения корня итерационный.
x2 = φ(x1)
xn+1 = φ(xn)
Счёт заканчивается при выполнении условия:
| xn+1-xn|<=eps или | f(xn+1)|<=eps
Условие, при котором данный процесс будет сходящимся, определяется следующей теоремой:
если интервал (a,b) является интервалом изоляции корня уравнения x=φ(x) и во всех точках данного интервала удовлетворяется условие
| φ(x)|<=q<1,
то процесс нахождения корня будет сходящимся, вычисления прекращаются при выполнении условия:
|xn+1-xn|<=(1-q)/q*eps
Где q-наименьшее значение | φ(x)| при изменении x: a<=x<=b
Очень важно при использовании данного метода преобразование уравнения f(x)=0 к уравнению вида x= φ(x) таким образом, чтобы итерационный процесс был сходящимся.
Метод Ньютона.
Метод основан на последовательном приближении к корню уравнения при заданных начальных условиях: начальное приближение и точность вычисления. В методе Ньютона осуществляется экстрополяция с помощью касательной к кривой в данной точке. В основе метода лежит разложение функции по формуле Тейлора. Члены, содержащие h во второй и более высоких степенях, отбрасываются. Для нахождения корня используется соотношение xn+1 = xn + h. Предполагается, что переход от xn к xn+1 приближает значение функции к нулю.
h = -f(x)/f’(x) тогда
xn+1 = xn -f(x)/f’(x)
Условие окончания счёта:
|xn+1-xn|<=eps
| f(xn+1)|<=eps
Очень важным при использовании данного метода является выбор начального приближения. Начальное приближение выбирается из условия
F(x0)*f’’(x0)>0
В противном случае сходимость итерационного процесса не гарантируется.
Схема Горнера.
Один из методов вычисления полинома – разложение его по схеме Горнера.
Полином
f(x) = antn + an-1tn-1 +… + a4t4+ a3t3+ a2t2+ a1t + a0
по схеме Горнера представляется в виде
f(x) = (((…(ant+ an-1)t +…+a4)t + a3)t + a2)t +a1)t + a0
Данное разложение полинома удобно тем, что в нём отсутствует возведение в степень, что значительно ускоряет вычисление полинома.
Блок-схема метода деления отрезка пополам:
да
нет
c=(a+b)/2
b=c
a=c
да
нет
да
нет
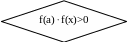
Блок-схема метода хорд:
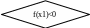Нет Да
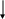
n:=x2
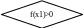Нет Да
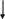
k:=n-f(n)(
n-x1)/ (f(n)- f(x1))
k:=n-f(n)(
x2-n)/(f(x2)-f(n))
Нет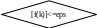 
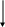
Д
n:=k
Блок-схема метода простой итерации:
Нет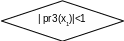 
k=(x1)
x1:=k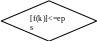
Нет
Да
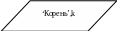
Блок-схема метода Ньютона:
xxxxx
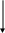
x:=x0
– fa(x0)/fq(x0)
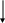
Нет
x0:=x
Да
Блок-схема схемы Горнера:
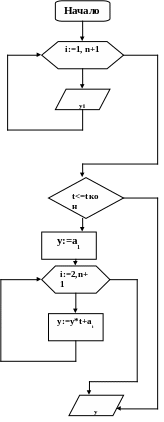
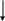
Листинг программы.
Program kurs;
uses crt,graph;
var GrMode,Grdriver:integer;
cc,j,i:integer;
s:string;
key:char;
prexit:boolean;
menu:array[1..5] of string;
function f(x:real):real;
begin
f:=exp(-x)-x;
end;
function p1(a,b:real):real;
var c:real;
const e=0.001;
begin
repeat
c:=(a+b)/2;
if f(a)*f(c)<0 then b:=c else a:=c;
until abs(a-b)<e;
p1:=a;
end;
function p2(a,b:real):real;
var x1,x0:real;
const e=0.001;
begin
if f(a)<0 then begin x1:=a;
repeat
x0:=x1;
x1:=x0-f(x0)*(b-x0)/(f(b)-f(x0));
until abs(x0-x1)<e; end
else begin x1:=b;
repeat
x0:=x1;
x1:=x0-f(x0)*(x0-a)/(f(x0)-f(a));
until abs(x0-x1)<e; end;
p2:=x1;
end;
function p3(q:real):real;
var x0,x1:real;
const e=0.001;
begin
x1:=q;
repeat
x0:=x1;
x1:=exp(-x0);
until abs(x0-x1)<e;
p3:=x1;
end;
function p4(q:real):real;
var x0,x1:real;
const e=0.001;
begin
x1:=q;
repeat
x0:=x1;
x1:=x0-f(x0)/(-exp(-x0)-1);
until abs(x1-x0)<e;
p4:=x1;
end;
procedure nl;
var a,b,q,l:real;
s:string;
begin
a:=0; b:=1; q:=0.5;
Outtextxy(100,100,'Reshenie nelineinogo uravneniya:');
Outtextxy(100,150,'Metod bisekcii: k = ');
str(p1(a,b),s); Outtextxy(320,150,s);
Outtextxy(100,200,'Metod hord: k = ');
str(p2(a,b),s); Outtextxy(320,200,s);
Outtextxy(100,250,'Metod prostyh iteracij: k = ');
str(p3(q),s); Outtextxy(320,250,s);
Outtextxy(100,300,'Metod Njutona: k = ');
str(p4(q),s); Outtextxy(320,300,s);
readkey;
end;
function kv:real;
var a,b,d,disk,x1,x2,r:real;
begin
a:=1; b:=-4; d:=3;
disk:=b*b-4*a*d;
x1:=(-b+sqrt(disk))/(2*a);
x2:=(-b-sqrt(disk))/(2*a);
if abs(x1)<abs(x2) then r:=x1 else r:=x2;
kv:=r;
end;
procedure kvadr;
var s:string;
begin
Outtextxy(100,100,'Naimenshij po absolutmomu znacheeniju koren uravneniya');
Outtextxy(100,150,'a*z*z+b*z+d=0');
Outtextxy(100,200,'pri a = 1, b = -4, d = 3');
str(kv:3:3,s);
outtextxy(100,250,'m = '); outtextxy(130,250,s);
readln;
end;
procedure graf;
const t0=0; tkon=115; tk=0.75;
var i:integer;
s:string;
p,q,c,k,m,o,gr,t:real; u,z: integer;
g:array[0..4] of real;
begin
p:=1; q:=cos(30*pi/180); c:=sin(35*pi/180);
cleardevice;
setcolor(green);
Outtextxy(100,50,'Znacheniya koefficientov osnovnoi funkcii');
setcolor(white);
str(p:3:3,s);
outtextxy(100,100,'p = ');outtextxy(150,100,s);
str(q:3:3,s);
outtextxy(100,130,'q = ');outtextxy(150,130,s);
str(c:3:3,s);
outtextxy(100,160,'c = ');outtextxy(150,160,s);
str(p1(0,1):3:3,s);
outtextxy(100,190,'k = ');outtextxy(150,190,s);
str(kv:3:3,s);
outtextxy(100,220,'m = ');outtextxy(150,220,s);
readkey; cleardevice;
setcolor(green);
rectangle(490,40,630,300);
rectangle(490,40,630,20);
line(530,20,530,300);
outtextxy(500,30,'t y');
setcolor(8);
for i:=1 to 15 do line(52,400-20*i,420,400-20*i);
for i:=1 to 12 do line(50+30*i,95,50+30*i,398);
setcolor(yellow);
line (50,5,50,400); line(50,400,470,400);
line (50,5,48,10); line (50,5,52,10);
outtextxy(470,410,'t');
line (470,400,465,398); line (470,400,465,402); setcolor(yellow);
outtextxy(60,10,'y*10^6 ');
for i:=1 to 120 do
if i mod 10 = 0 then
begin
line(50+3*i,398,50+3*i,402);
str(i,s);
outtextxy(40+3*i,410,s);
end;
outtextxy(45,410,'0');
for i:=1 to 16 do
begin
line(48,400-20*i,52,400-20*i);
str(0.1*i:3:1,s);
outtextxy(10,395-20*i,s);
end;
t:=t0;
u:=50; z:=400-round(abs((p1(0,1)+kv)/5000));
g[1]:=p;
g[2]:=q;
g[3]:=c;
g[4]:=kv+p1(0,1);
repeat
if t>tkon then t:=tkon;
gr:=0;
for i:=1 to 3 do
gr:=(gr+g[i])*t;
gr:=gr+g[4];
setcolor(white);
if frac(t/5)=0 then begin
str(t:2:0,s);
outtextxy(495,round(50+2*t),s);
str(abs(gr):3:1,s);
outtextxy(550,round(50+2*t),s); end;
setcolor(red);
line(u,z,round(50+3*t),(400-round(abs(gr)/5000)));
u:=round(50+3*t); z:=400-round(abs(gr)/5000) ;
if t<>tkon then t:=t+tk;
if cc=3 then delay(100);
until t=tkon;
readln;
end;
begin
GrDriver:=detect;
initgraph(GrDriver,GrMode,' ');
cleardevice;
setcolor(white);
menu[1]:=' Reshenie kvadratnogo uravneniya ';
menu[2]:=' Reshenie nelineynogo uravneniya ';
menu[3]:=' Grafik v realnom vremeni ';
menu[4]:=' Grafik v mashinnom vremeni ';
menu[5]:=' Vyhod iz programmy ';
cc:=1;
prexit:=false;
repeat
begin
setcolor(8);
cleardevice;
end;
Setcolor(4+127);
Outtextxy(170,100,'Menu');
for i:=1 to 5 do begin setcolor(green);
if i=cc then setcolor(6) else setcolor(yellow);
outtextxy(150,200+20*i,menu[i]);end;
key:=readkey;
case ord(key) of
13:begin cleardevice;
case cc of
1:kvadr;
2:nl;
3:graf;
4:graf;
5:prexit:=true; end;end;
72:dec(cc);
80:inc(cc); end;
if cc<1 then cc:=5;
if cc>5 then cc:=1;
until prexit;
closegraph;
end.
Результаты расчетов:
T |
Y |
0.0 |
1.6 |
15 |
3580.0 |
30 |
27798.2 |
45 |
92906.1 |
60 |
219153.7 |
75 |
426791.0 |
90 |
736068.0 |
105 |
1167234.7 |
115 |
1532395.7 |