1.

Математическое моделирование называется процесс составления математич. одели, решение любой задачи невозможно без математ-кой модели. Для этого нужно : 1) выделить учавствующие задачи и величины 2) определить какте величины неизвестны, какие найти 3) определить взаимозависимости между величинами, если они есть

Каждая модель содержит много факторов.Требования, предъявляемые к математической модели. Основные требования следующие:

1) Достаточность означает, что модель должна содержать достаточно величин и соотношений , чтобы получить решение задач.

2) Адекватность означает , что расчетные результаты должны соответствовать - не обязательно совпадать действительным

3) Корректность - сложное требование. В понятие корректность

входит 3 составные части:

разрешимость, единственность, и устойчивость.

Разрешимость означает, что решение должно быть.

Под единственностью понимается единственность решения. Устойчивость означает, что малые изменения начальных данных не должны приводить к большим изменениям результата. Основные типы задач, возникающих при математическом моделировании

1) Решение алгебраических, линейных, трансцендентных уравнений и систем уравнений.

2) Решение диф. Уравнений и систем диф. Уравнений.

3) Обработка результатов эксперимента.Аппроксимация (приближение) функций.

4) Решение задач оптимизации.

5) Решение интегральных уравнений и систем таких иуравнений. И т.Д.

6) Планирование эксперимента.

7) Задачи оптимизированного управления и др.

13.

Интерполяцией называют отыскание видов функций f(x) мет.узлами таб. По зада.значениям f(x1) в узлах таблицы, получ.формул,работает только для [x1,xn]

Рассмотрим таблицу значений х,у Х х1 х2 … хn

У у1 у2 … уn

Известно,что х зависит от у , причем f(xk)=yk,k=1,2,..n. Интерпол.многочлен Лагранжа Lk(x)-это единст.

Многочлен.степени не выше <=n-1, который выч.по формуле

n

Lk(x)=Σ yklk(x) , где уn из таблицы k=1 Lk(x)=(x-x1)(x-x2)(..)(x-x k-1)(x- x k+1) ..(x-xn) /

(xk-x1)(xk-x2)(…)(xk- x k-1) (x- x k+1) .. (xk-xn)

Причем выполняется условие , что Lk(xi)= 1,k=i 0,k≠i Известно , что для многочл.Лагранжа выполняется условие Lk(xk)=yk

2.

Чаще применяют численные методы, при этом возникают различные ошибки-погрешности. Различают: погрешности метода, начальные погрешности, остаточные погрешности, погрешности округления . Еще сущ-ют абсолютные и относительные погрешности Пусть х-число x̃ –его приближенное значение Тогда абсолютной погрешностью называют величину Δх=|х- x̃ |, а относительной

x̃ =х- x̃/| x̃ | = Δх /| x̃ При решении числ-ми методами точное значение х неизвестно,поэтому невозможно вычислить погрешность, в таких случаях ищут предельные погрешности. если сущ-ет величина Δ x̃ , что |Δx|<|Δ x̃ | , то Δ x̃ наз-ся предельной абсолютной погрешностью, а δ Δ x̃= Δ x̃ /| x̃ | - предел.относит.погрешность Численные методы решения нелинейных ур-ний f(x)=0 Решаем ур-е f(x)=0, если f(x)-нелинейн.функ.,то ур-е будет назыв.нелинейным,в частных случаях,например,f(x)=ax²+bx+c и др.оно решается точно,чаще оно точно не решается,числин.методы,называемые итерационными+шаг,такие методы выполн.в 2 этапа:

1)ищут приближенные решения или отрезка [а,в] с одни корнем ур-я f(x)=0 2)уточняют приближенное решение до заранее заданной точности ε(малое)ε=0.001 при этом говорят , что ур. f (x)=0 решено с точностью ε

3.

Для уравн. F(x)=0 находим обычно графически отрезок [а,в] с одним корнем, должно выполняться условие f(a)·f(b)<0 – условие выбора [а,в] Затем делим [а,в] пополам х0=а+в/2 →[а;х0] и [х0;в] оставляем тот,на концах которого f(x) имеет разные знаки , другой отбрасываем Пример :

Новый отрезок снова делим пополам х1=а+х0/2 →[а;х1] и [х1;х0] …. продожаем до тех пор , пока на каком-то шаге не выполнится одно из условий окончаний итер-ного процесса: а) |х к+1 - хк| <= ε б) | f(xk)| <= ε Достоинства: можно решить ур-е с любой точностью Недостатки: трудоемкость,медленная сходимость

4.

Известно , что ур-е 1-ой касательной имеет вид у1-у0=f ′ (x0)(x1-x0) т.к. у0=f(x0) у1≈0 ,т.к. f(х)=0 , то х1=х0 - f(x0)/ f ′ (x0) x2= x1- f(x1)/ f ′ (x1) итер.ф-ла Ньютона х к+1 = хк - f(xк)/ f ′ (xк) х0 выбираем из условия f(х0) · f ′′(х0)>0 Достоинства: быстрая расходимость при удачном выборе х

Недостатки: метод применим только дл ф-ции f ′ , f ′′ , причем f ′ (xк) ≠0

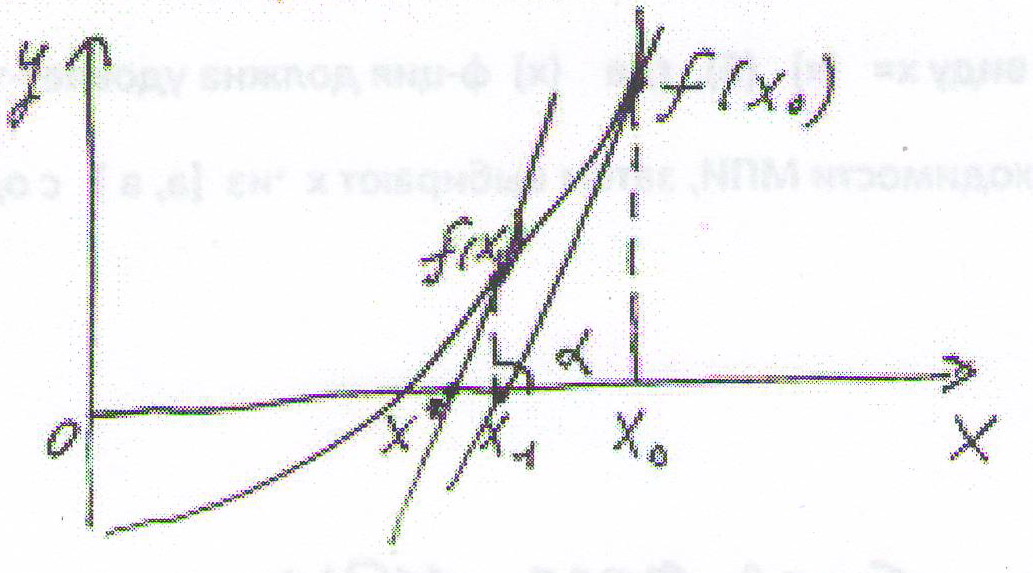
5. ур-е f(x)=0 приводят к виду х=ψ(х), где ψ(х)-ф-ция должна удовлетворять условию 0<|ψ(x)|<1 – условие сходимости МПИ , затем выбирают х из [а,в] с одним корнем ур-ния f(x)=0 х1= ψ(х0), х2= ψ(х1) х к+1 = ψ(хк) – итер.формула МПИ Решение продолжают пока не выполниться условие а) |x к+1 -хк| <=ε б) |f(xk)|<=ε , перейти от 1 к 6 можно по разному : |: обе части f(x)=0 на - N , и прибавив к обеим частям Х

- f(x)/ N=0 x- - f(x)/ N= 0+X x=x- f(x)/ N N найдем из условия сходимости 0< |1 - - f ′ (x)/ N| <1 затем примен.формул. x к+1= хл- f(xк)/ N

6

Метод Гаусса состоит из прямого и обратного хода

В прямом СЛАУ приводиться к треугольному виду. В обратном ищется неизвестные начиная с последнего

Метод Крамера решение ищут по формуле:

Xj=Dj/D

D=DltA не равно 0 Dj определители получаются из D после замены j

Столбца на столбец правой части

Пример

5x+y=6 5x+x2=6

x-4y=3 x1-4x2=-3

A=(5 1) D1=(6 1)

(1-4) ( -3-4) =-21

D=dltA=5 1=-21

1 -4

D2=5 6=-21

1 -3

X1=D1/D=1 x2=D2/D=1

Берем программу из двух функций

A11x1+a12x2=b1

A21x1+a22x2=b2

INPUT

A11,a12,b1,a21,a22,b2

D=a11*a22-a12*a21

D1=b1+a22-b2*a12

D2=…

X1=D1/D

X2=D2/D

Print x1,x2

7

Метод прогонки яв-ся модефикацией метода Гаусса. Применяется только для СЛАУ с 3-х диагональной ленточной матрицей,такие СЛАУ имеют вид:

акх к-1 +вкхк+скх к-1=dк а1=0 сn=0 к=1,2,..n (1) Здесь а,в,с,d –известные , х,к-неизвестные Запишем СЛАУ при n=3 к=1 в1х1+с1х2 =d1

к=2 а2х1+в2х2+с2х3= d2 к=3 а3х2+в3х3= d3 Метод прогонки имеет прямой ход и обратный – в прямом ищут прогоночные коэф.-ты, в обратном находят неизвестные,начиная с последнего . решение ищут по ф-ле хк=uкх к-1 +vк (2)

Прямой ход

Найдем Uk и Vk для этого подставим в (1) замену для хк-1, полученной из (2) ак(u к-1 хк+v к-1)+вкхк+скх к-1=dk (ак u к-1+вк)хк= dk - скх к-1-акvк-1

Найдем хк= -ск/ак u к-1+вк · х к-1 +dk-akvk-1/ak u к-1+bk

Сравнивая эту формулу с (2) хк=uk x к-1 +vk

Uk= - ck/ak u к-1 +b1

Vk=dk-akv к-1/ak u к-1+bk

U1=c1/b1 u2=- c2/a2u1+b2

V1=d1/b1 v2=d2-a2v1/a2u1+b2

Ur=0

Vk=dk-ak·v к-1 /ak u к-1+bk

Uk=-ck/ak u к-1+bk

Vk=dk-akv к-1/ak u к-1+bk

Найдем неизвестные начиная с последнего

Xk=uk x к+1 +vk

Xn=un x к+1 +vn=vn

x n-1 = u n-1 xn+ vк-1= u n-1 vn + vк-1

x1=u1x2+v1