
- •30. Собственные векторы линейного преобразования. Вид матрицы линейного преобразования в базисе из собственных векторов
- •31. Диагонализируемые линейные преобразования. Достаточные условия диагонализируемости линейного преобразования
- •32. Симметричные линейные преобразования, их свойства
- •33. Расстояние между точками на числовой прямой, окрестность точки. Определение функции
- •34. Предел последовательности: определение, свойства. Число
- •35. Предел функции: определение, свойства. Замечательные пределы
- •36. Непрерывность функции в точке: определение, теорема о приращении
- •37. Непрерывные функции, их свойства
- •38. Свойства непрерывных на замкнутом отрезке функций
- •39. Точки разрыва
- •40. Бесконечно малые величины
- •41. Определение производной. Геометрический смысл производной. Связь непрерывности и дифференцируемости функции
- •42. Правила дифференцирования. Производная сложной функции
- •43. Дифференциал: определение, геометрический смысл
- •48. Достаточные условия существования экстремума в терминах первой и второй производной
34. Предел последовательности: определение, свойства. Число
Определение
Числовая последовательность – это
отображение
![]() ,
т.е.
,
т.е.
![]()
![]() .
Каждому натуральному числу (номеру)
ставится в соответствие действительное
число. Последовательность обозначается
.
Каждому натуральному числу (номеру)
ставится в соответствие действительное
число. Последовательность обозначается
![]() или
или
![]()
Пример
![]() :
:
![]()
Определение
Число
называется пределом
последовательности
(обозначается
![]() ),
если для любого
существует номер
),
если для любого
существует номер
![]() ,
такой что для
,
такой что для
![]()
![]() или
или
![]() (или
(или
![]() ).
).
Теорема
Предел
![]() = этой
:
для последовательности
= этой
:
для последовательности
![]()
![]() .
.
Доказательство
Для любого
![]() .
.
Теорема (единственность предела последовательности)
Если существует предел последовательности
,
равный
,
и существует предел последовательности
.
Тогда
![]() .
.
Доказательство
![]() Существует
:
Существует
:
![]() (
(![]() ).
).
Для достаточно больших
![]() и
и
![]() - противоречие, так как это пересечение
пустое.
- противоречие, так как это пересечение
пустое.
Арифметические свойства предела последовательности
Пусть
![]() и
и
![]() .
Тогда
.
Тогда
1. Предел
![]()
2.
![]()
3.
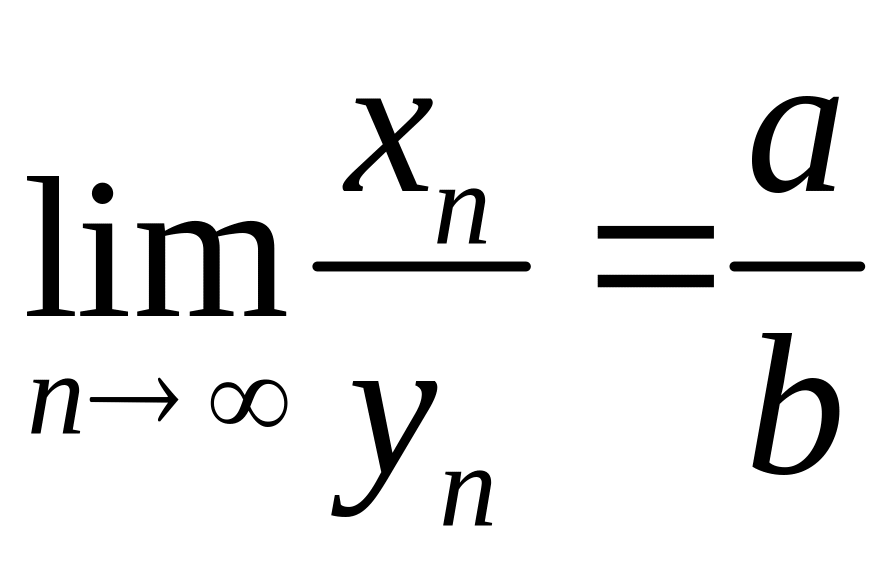 ,
если все
,
если все
![]() и
и
![]() .
.
Теорема о существовании предела монотонной ограниченной последовательности
Пусть
![]()
(или
![]() )
)
Тогда существует предел такой
последовательности и этот предел
![]() (или
(или
![]() )
)
Пример
Рассмотрим последовательность

Отметим, что
![]() ,
значит по теореме выше
,
значит по теореме выше
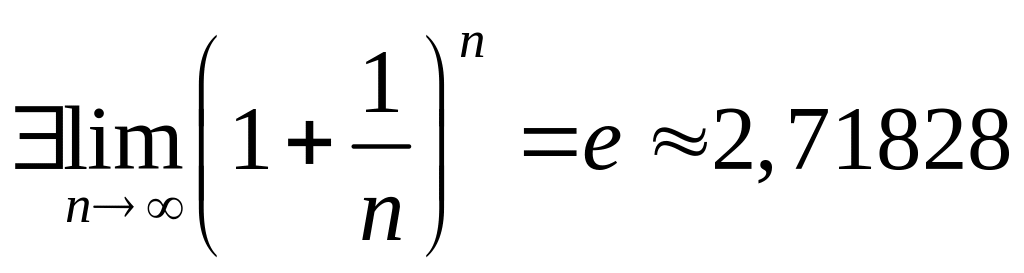
[_]
35. Предел функции: определение, свойства. Замечательные пределы
Определение
Число
![]() называется пределом функции
при
называется пределом функции
при
![]() (возможно, что
(возможно, что
![]() - области определения), если для любой
последовательности
- области определения), если для любой
последовательности
![]() значений аргумента, такой, что
значений аргумента, такой, что
![]() ,
,
![]() и
и
![]() ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
![]() имеет предел
:
имеет предел
:
![]() .
Сокращено
.
Сокращено
![]() для любой
:
выполняется
для любой
:
выполняется
Свойства предела функции
(аналогичны свойствам предела последовательности)
Пусть
![]() и
и
![]() .
Тогда
.
Тогда
1. Предел
![]()
2.
![]()
3.
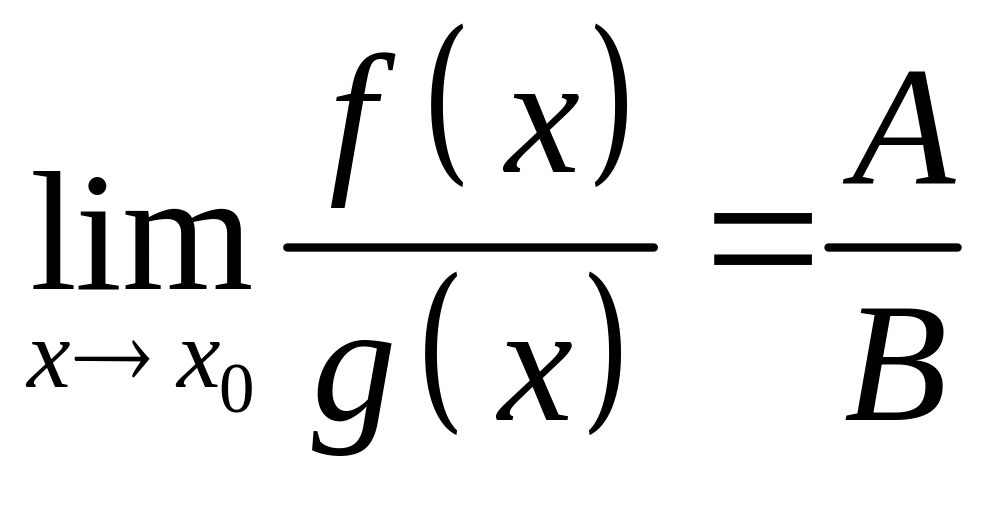 ,
если
,
если
![]() на всей области определения и
на всей области определения и
![]() .
.
Предельный переход в неравенствах
Пусть в некоторой окрестности точки
![]()
![]() для любого
для любого
![]() .
Если существует
.
Если существует
![]() и существует
и существует
![]() ,
то
,
то
![]()
Замечательные пределы
1.
![]()
2.
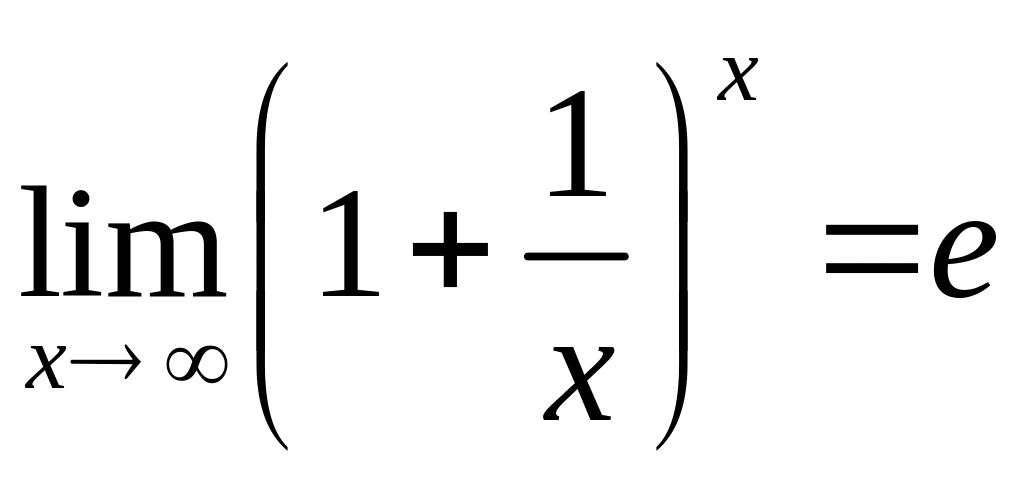
[_]
36. Непрерывность функции в точке: определение, теорема о приращении
Определение
Функция
непрерывна в точке
![]() ,
если
,
если
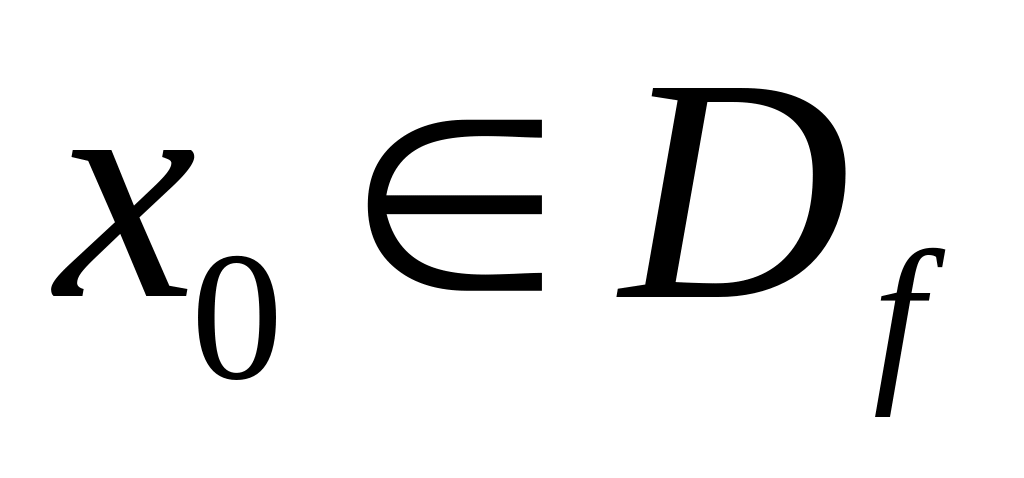 (
(
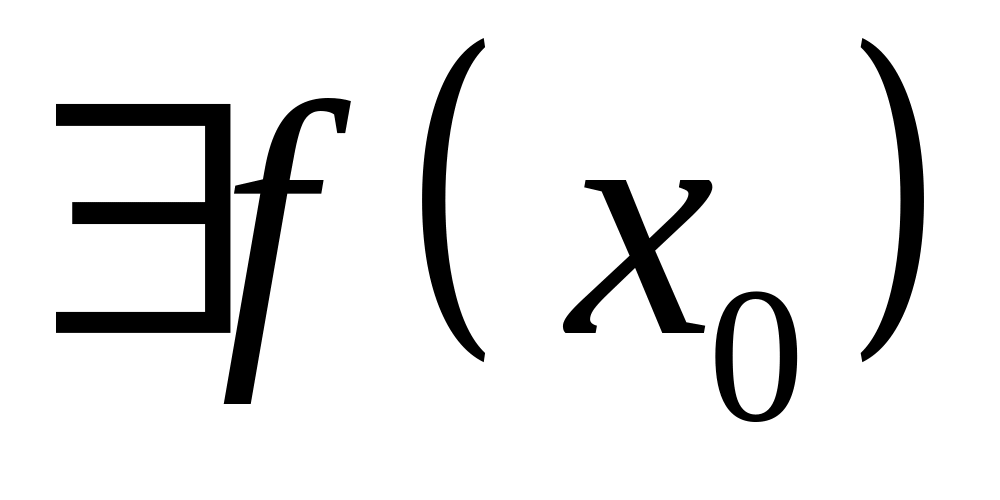 )
)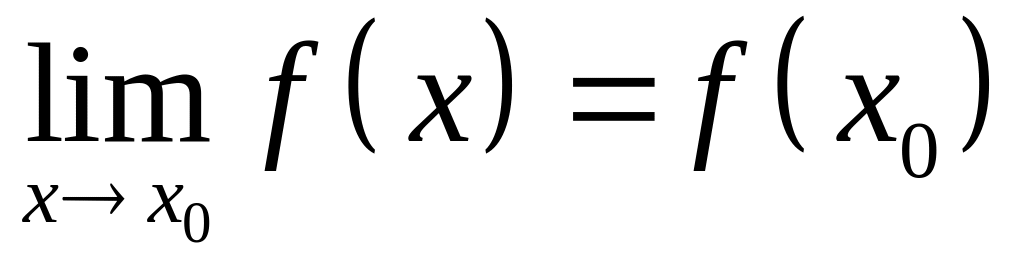
Определение
Пусть
,
- близкая к
точка,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() - приращение (изменение). Так как
,
то
- приращение (изменение). Так как
,
то
![]() .
.
![]()
![]() - приращение функции при переходе от
к
:
- приращение функции при переходе от
к
:
![]()
Теорема
Функция
непрерывна в точке
![]() .
.
Доказательство
![]() непрерывна в
непрерывна в
![]()
![]()
![]()
![]() .
.
[_]
37. Непрерывные функции, их свойства
Определение
Функция называется непрерывной, если она непрерывна в каждой точке - ее области определения.
Теорема
Каждая элементарная функция непрерывна (в ее области определения).
Теорема
Если функции
и
![]() непрерывны, то следующие функции также
непрерывны:
непрерывны, то следующие функции также
непрерывны:
![]() ,
,
![]() ,
,
![]() (при
)
(при
)
Теорема о непрерывности сложной функции
Пусть функция
![]() непрерывна в
,
а функция
непрерывна в
,
а функция
![]() непрерывна в
непрерывна в
![]() .
Сложная функция
.
Сложная функция
![]() непрерывна в
:
непрерывна в
:
![]()
![]()
![]() непрерывна в
.
непрерывна в
.
[_]
38. Свойства непрерывных на замкнутом отрезке функций
![]()
![]()
Теорема
Непрерывная на замкнутом отрезке
![]() функция
принимает на
свое наименьшее значение
функция
принимает на
свое наименьшее значение
![]() и наибольшее значение
и наибольшее значение
![]() ,
т.е.
,
т.е.
![]() такие, что
такие, что
![]() и
и
![]() .
.
Теорема
Пусть функция
непрерывна на
и принимает на его концах значения
разных знаков:
![]() .
Тогда
.
Тогда
![]() .
.
[_]
