Интегральный признак Коши.

Пусть - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале , где ). Тогда в случае сходимости несобственного интеграла 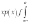сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится. При проверке убывания функции y = f(x) на интервале Вам может пригодится теория из раздела возрастание и убывание функции. Пример. Исследуйте числовой ряд с положительными членами на сходимость. Решение. Необходимое условие сходимости ряда выполнено, так как 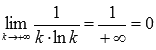. Рассмотрим функцию . Она положительная, непрерывная и убывающая на интервале . Непрерывность и положительность этой функции не вызывает сомнения, а на убывании остановимся чуть подробнее. Найдем производную: 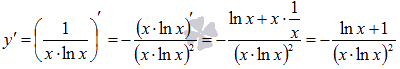. Она отрицательная на промежутке, следовательно, функция убывает на этом интервале. Таким образом, функция удовлетворяет всем условиям интегрального признака Коши. Воспользуемся им: 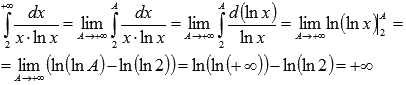То есть, несобственный интеграл расходится, следовательно, расходящимся является исходный числовой ряд.

Интегральный признак Коши

Постановка решения. Исследовать сходимость ряда с положительными членами

,

где , причем первообразная функции  легко вычисляется.

План решения.

Если , причем первообразная функции  легко вычисляется, то применяем интегральный признак Коши:

Если функция , принимающая в точках  значения , убывает в некотором промежутке , то ряд  и несобственный интеграл 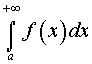 либо оба сходятся, либо оба расходятся одновременно.

1. Проверяем, что , т.к. если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Упрощаем, если требуется, выражение для , т.е. будем исследовать сходимость ряда , такого, что  при   и  выбраны так, чтобы функция  имела очевидную первообразную . Затем используем вторую теорему сравнения.

3. Исследуем сходимость несобственного интеграла по определению

.

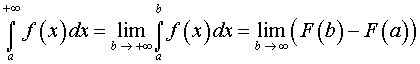4. Применяем интегральный признак Коши к ряду

и затем делаем вывод о сходимости или расходимости исходного ряда , используя вторую (предельную) теорему сравнения.

Замечание. Интегральный признак Коши применяется в частности к рядам вида .

Задача 7. Исследовать на сходимость ряд.

.

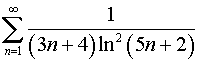Сравним данный ряд с рядом . Мы можем это сделать согласно предельному признаку сравнения:

.

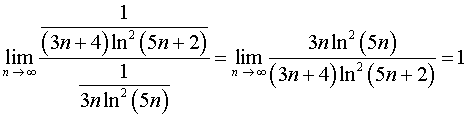Воспользуемся интегральным признаком Коши:

Ряд  сходится, значит сходится и исследуемый ряд.

12 необходимое условие сходимости ряда

Достаточные признаки условной сходимости числового ряда. Признак Лейбница.

Если абсолютные величины членов знакочередующегося ряда монотонно убывают и предел модуля общего члена ряда равен нулю при , то ряд сходится. Пример. Определите характер сходимости знакочередующегося числового ряда . Решение. Ряд из абсолютных величин членов имеет вид 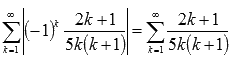. Для него выполняется необходимое условие сходимости . Возьмем гармонический ряд и воспользуемся вторым признаком сравнения: Таким образом, ряд из модулей - расходящийся. 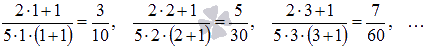В свою очередь, знакочередующийся ряд сходится, так как выполняются условия признака Лейбница: последовательность монотонно убывает и . Следовательно, исходный ряд условно сходящийся.

Последовательность u₁+u₂+...+u_n+... сходится, когда общий член ряда u_n стремится к нулю:

Lim u_n = 0

^n->∞

Это неободимое, но не достаточное условие. Например, гармонический ряд 1+1/2+1/3+1/4+ расходится. Здесь общий член стремится к 0, а частичная сумма неограниченно возрастает.

положительный ряд

ряд, все члены которого положительны. Если его частичные суммы имеют предел, то положительный ряд сходится, иначе расходится.