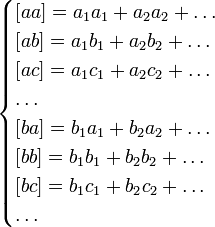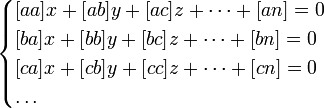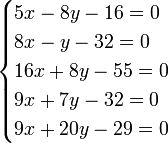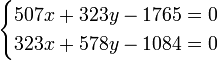1 Предел функции двух переменных. Определение. Число A называет пределом функции   при стремлении точки M к точке  , если для любого ε>0 существует такое δ>0, что для всех точек M из области определения этой функции, удовлетворяющих условию   имеет место неравенство  . Обозначают это так:   или  Функция   называется бесконечно малой при   если   Непрерывность функции двух переменных. Пусть точка   принадлежит области определения  . Определение. Функция   называется непрерывной в точке   если   или   причем точка M стремится к M₀ произвольным образом, оставаясь  в области определения функции.  Обозначим  ,  . Полным приращением   при переходе от точки  , к точке M называется разность значении функции в этой точке  , т.е. 

2Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных   в точке   частные производные определяются так: ,        ,       если эти пределы существуют. Величина                           называется частным  приращением функции z в точке   по аргументу  . Используются и другие   обозначения частных производных:              ,   ,       ,        ,              ,   ,       ,        .       Из определения следует геометрический смысл частной производной функции двух переменных: частная производная   -угловой коэффициент касательной к линии пересечения поверхности    и плоскости                            в соответствующей точке.        Пользуясь понятием скорости изменения переменной, можно сказать, что частная производная   есть скорость изменения функции   относительно   при постоянном  . Необходимое условие дифференцируемости: если функция дифференцируема в точке  ,то она непрерывна в этой точке.производная.

3 Полный дифференциал.        .  (1)       Если приращение (1) можно представить в виде        , (2) Где Аи В не зависят от   и  , а   и   стремятся к нулю при стремлении к нулю   и  , то функция   называется дифференцируемой в точке  , а линейная часть   приращения функции (т.е. та часть  , которая зависит от    и   линейно) называется полным дифференциалом (или просто дифференциалом) этой функции в точке   и обозначается символом  :                                     .   

 достаточное условие дифференцируемости. Если функция   имеет частные производные в некоторой окрестности точки   и эти производные непрерывны в самой точке  , то эта функция дифференцируема в точке  .     

4      Частные производные высших порядков.           Частные производные функции нескольких переменных сами являются функциями этих переменных и могут иметь частные производные. Для исходной функции эти последние производные будут частными производными второго порядка. Так, для функции   двух независимых переменных можно определить (предполагается, что все производные существуют) четыре частные производные второго порядка, которые обозначаются символами            ,          ,            ,        .  Частные производные   и  , отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка

Дифференциалы высших порядков.              Заметим прежде всего, что для функции нескольких переменных справедливы те же общие правила дифференцирования, что и для функции одной переменной: I.      , . II.  . III.    . IV.    .

5 Экстремум функции двух переменных

 

Говорят, что функция   имеет максимум в точке  , т.е. при   , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Говорят, что функция   имеет минимум в точке  , т.е. при  , если   для всех точек  , достаточно близких к точке   и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. 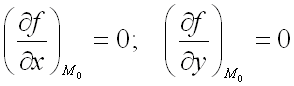, тогда при  : 1)   имеет максимум, если дискриминант   и  , где 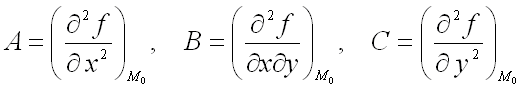 ; 2)   имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

6 Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Пусть надо решить систему уравнений

(1)

число которых более числа неизвестных x, y,

Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д. Если обозначить для краткости:

то нормальные уравнения представятся в следующем простом виде:

(2)

Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д. Для пояснения сказанного ниже приведено решение пяти уравнений с двумя неизвестными:

Составив значения [aa], [ab], получаем следующие нормальные уравнения:

,

Проще говоря перемножается матрица X и транспонированная матрица Xт. Размерности этих матриц 3x6 и 6x3, соответственно в итоге получается матрица 3x3, которая и есть итоговое уравнение.

откуда

x = 3,55;

y = − 0,109