
- •5 Экстремум функции двух переменных
- •7 Бесконечным числовым рядом называется выражение
- •9 Признак Даламбера Признак Даламбера.
- •Интегральный признак Коши.
- •Интегральный признак Коши
- •Достаточные признаки условной сходимости числового ряда. Признак Лейбница.
- •13. Исследование знакопеременных рядов на абсолютную сходимость.
7 Бесконечным числовым рядом называется выражение
u1+u2+...+un+... , |
(1) |
содержащее неограниченное число членов, где
u1 , u2 , u3 , ... , un , ...
- бесконечная числовая последовательность; un называется общим членом ряда. Для составления ряда нужно знать закон образования общего члена.
1).
Если ![]() ,
то
,
то ![]() при
при 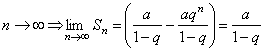 .
Значит, в случае
.
Значит, в случае ![]() ряд
(98) сходится и его сумма
ряд
(98) сходится и его сумма ![]() .
.
2).
Если ![]() ,
то
,
то ![]() и
тогда
и
тогда ![]() при
при ![]() ,
т.е.
,
т.е. ![]() не
существует. Таким образом, в случае
ряд
(98) расходится.
не
существует. Таким образом, в случае
ряд
(98) расходится.
3)
Если ![]() ,
то ряд (98) имеет вид:
,
то ряд (98) имеет вид: ![]() .
В этом случае
.
В этом случае ![]() ,
т.е. ряд расходится.
,
т.е. ряд расходится.
Если ![]() то
то ![]() .
В этом случае:
.
В этом случае: ![]()
8
Необходимый признак сходимости
числового ряда.
Гармонический
ряд.
Нахождение n-й частичной
суммы ![]() и
ее предела для произвольного ряда во
многих случаях является непростой
задачей. Поэтому для выяснения сходимости
ряда устанавливают специальные признаки
сходимости. Первым из них, как правило,
является необходимый признак
сходимости.
Теорема.
Если
ряд
и
ее предела для произвольного ряда во
многих случаях является непростой
задачей. Поэтому для выяснения сходимости
ряда устанавливают специальные признаки
сходимости. Первым из них, как правило,
является необходимый признак
сходимости.
Теорема.
Если
ряд ![]() сходится,
то его общий член
сходится,
то его общий член ![]() стремится
к нулю, т.е.
стремится
к нулю, т.е. ![]() .
Пусть
ряд
сходится
и
.
Пусть
ряд
сходится
и ![]() .
Тогда и
.
Тогда и ![]() .
Учитывая, что
.
Учитывая, что ![]() при n>1,
получаем:
при n>1,
получаем:
![]() .
Следствие (достаточное
условие расходимости ряда)
Если
.
Следствие (достаточное
условие расходимости ряда)
Если ![]() или
этот предел не существует, то ряд
расходится.
Действительно, если бы
ряд сходился, то (по теореме)
.
Но это противоречит условию. Значит,
ряд расходится.
Теорема о сходимости
дает необходимое условие сходимости
ряда, но не достаточное: из условия
не
следует, что ряд сходится. Это означает,
что существуют расходящиеся ряды, для
которых
или
этот предел не существует, то ряд
расходится.
Действительно, если бы
ряд сходился, то (по теореме)
.
Но это противоречит условию. Значит,
ряд расходится.
Теорема о сходимости
дает необходимое условие сходимости
ряда, но не достаточное: из условия
не
следует, что ряд сходится. Это означает,
что существуют расходящиеся ряды, для
которых
9 Признак Даламбера Признак Даламбера.
Пусть
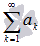 -
знакоположительный числовой ряд. Если
-
знакоположительный числовой ряд. Если
 ,
то числовой ряд сходится, если
,
то числовой ряд сходится, если
 ,
то ряд расходится.
Замечание.
Признак
Даламбера справедлив, если предел
бесконечен, то есть, если
,
то ряд расходится.
Замечание.
Признак
Даламбера справедлив, если предел
бесконечен, то есть, если
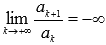 ,
то ряд сходится, если
,
то ряд сходится, если
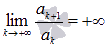 ,
то ряд расходится.
Если
,
то ряд расходится.
Если
 ,
то признак Даламбера не дает информацию
о сходимости или расходимости ряда и
требуется дополнительное
исследование.
Пример.
Исследуйте
числовой ряд
,
то признак Даламбера не дает информацию
о сходимости или расходимости ряда и
требуется дополнительное
исследование.
Пример.
Исследуйте
числовой ряд
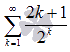 на
сходимость по признаку
Даламбера.
Решение.
Проверим
выполнение необходимого условия
сходимости числового ряда, предел
вычислим по правилу
Лопиталя:
на
сходимость по признаку
Даламбера.
Решение.
Проверим
выполнение необходимого условия
сходимости числового ряда, предел
вычислим по правилу
Лопиталя:
 Условие
выполнено.
Воспользуемся признаком
Даламбера:
Условие
выполнено.
Воспользуемся признаком
Даламбера:
 Таким
образом, ряд сходится.
Таким
образом, ряд сходится.
(2) Пусть дан ряд
u1+u2+u3+...+un+... , |
(1) |
с положительными членами. Относительно этого ряда имеют место две следующие теоремы Даламбера.
Теорема 1. Если отношение каждого последующего члена ряда (1) к предидущему члену меньше фиксированного числа q<1 (или равно q), то ряд (1) сходится; если это отношение больше 1 (или равно 1), то ряд (1) расходится. Признак Даламбера (продолжение)
Теорема 2. Пусть l - предел отношения последующего члена un+1 ряда (1) к предидущему un при n®Ґ , т.е.

Тогда, если l < 1, то ряд l сходится, если l > 1, то ряд l расходится, Если же l = 1, то вопрос о сходимости ряда (1) остается открытым.
10
(Признак Коши).
Если величина ![]() имеет
конечный предел
имеет
конечный предел ![]() при
,
т.е.
при
,
т.е.
 ,
,
то 1) при < 1 – ряд сходится;
2) при > 1 – ряд расходится.
Исследовать сходимость
числового ряда:
![]() Решение
Условия
признака Лейбница выполнены:
Решение
Условия
признака Лейбница выполнены:
 Исследуем
на сходимость ряд
Исследуем
на сходимость ряд
![]() Применим
радикальный признак Коши:
Применим
радикальный признак Коши:
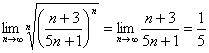 ряд
сходится
Таким образом, ряд
сходится
абсолютно.
ряд
сходится
Таким образом, ряд
сходится
абсолютно.
11.
