Билет1

1)Двойной интеграл: Предел интегральных сумм (1) при  → 0 называется двойным интегралом и обозначается или

Площадь пластинки

Объём тела

Масса

Пусть γ(x,y,z) -- плотность тела V в точке (x,y,z). Тогда его масса M равна

Пусть γ (x,y) -- поверхностная плотность пластинки D в точке (x,y). Тогда её масса M равна

Пусть тело V задано так

Тогда объём этого тела равен .

Необходимое условие интегрируемости.Если функция интегрируема на отрезке, то она ограничена на нем. 

Свойство 1. Двойной интеграл суммы двух функций равен сумме двойных интегралов.

Свойство 2. Постоянный множитель можно выносить за знак двойного интеграла.

Свойство 3 (аддитивность)} Если область D разбить на две области D_1 и D_2 так, что пересечение D_1∩ D_2 -- кривая, то ∬_D=∬_{D_1}+∬_{D_2}.

 Оценки интегралов 

     1. Если   то

 Теорема о среднемЕсли f непрерывна на [a,b], то

2) дробно-линейнойФункция вида , где a,b,c,d∈ℂ и ad-bc≠ 0,

Инверсия

Преобразование евклидовой плоскости, переводящее всякую точку P, не совпадающую с O в инверсную точку P', называется инверсией. Рассмотрим лишь случай, когда P лежит вне круга. Проводим касательную к окружности γ из точки P. Пусть A -- точка касания. Опускаем перпендикуляр из точки A на луч OP. Инверсная точка P' будет основанием этого перпендикуляра. Это следует из подобия треугольников OAP' и OAP:

OA/ OP= OP'/OA, откуда R²=OA²=OP⋅OP'.

При инверсии центр круга переходит в бесконечно удаленную точку. Наоборот, если P→ ∞ , то P'→ O.

Теорема [круговое свойство] Всякая дробно-линейная функция переводит окружность в расширенном смысле в окружность в расширенном смысле.

Предложение 1. Дробно-линейная функция, отображающая верхнюю полуплоскость на внутренность единичного круга имеет вид

Предложение 2. При любом дейсвительном и любом комплексном α, не принадлежащем единичной окружности, дробно-линейная функция следующего вида:

отображает единичную окружность на себя. Если , то (3) отображает единичный круг на себя, а при (3) отображает единичный круг на внешность единичного круга.

Предложение 3.Группа дробно-линейных преобразований, оставляющих верхнююполуплоскось на месте, состоит из функций вида

Билет 2

1) Поставим задачу -- найти массу нити L, заданной параметрически x=x(t), y=y(t), z=z(t), если  ≤ t≤  и имеющей линейную плотность γ (x,y,z). Дифференциал массы находится так

dM=γ dl=γ (x,y,z)\sqrt{d^2x=d^2y=d^2z}=γ (x(t),y(t),z(t))\sqrt{x'^2+y'^2+z'^2}dt

Отсюда получаем ответ

Пусть  =t_0<t_1<...<t_n= -- разбиение, ξ _i\in[t_{i-1},t_i] -- отмеченные точки. Обозначим Δ s_i=\sqrt{(x(t_i)-x(t_{i-1}))^2+(y(t_i)-y(t_{i-1}))^2+(z(t_i)-z(t_{i-1}))^2} Тогда, по определению криволинейный интеграл по длине дуги это

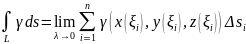
Свойства как у обычного интеграла.

Имеется кривая L в пространстве с началом M и концом N и векторное поле F на L. Разобьём L точками M=M_0,M_1,...,M_n=N. Параметром этого разбиения}  назовём величину max_i{|Δ S_i|}. Обозначим \Delta S_i=\ar{M_iM_{i+1}}. Составим интегральную сумму}

\sum_iF_i\Delta S_i (1)

Криволинейным интегралом поля F по кривой L (обозначается ) называется предел интегральных сумм (1), если  → 0.

Замечание. Криволинейный интеграл -- работа силового поля F по перемещению материальной точки вдоль L.

Пусть F=X(x,y,z)\bi+Y(x,y,z)\bj+Z(x,y,z)\bk и M_i(x_i,y_i,z_i). Тогда

\Delta S_i=Δ x_i\bi+Δ y_i\bj+Δ z_i\bk и

\sum_iF_iΔS_i=\sum_i (X(x_i,y_i,z_i)Δx_i+Y(x_i,y_i,z_i)Δy_i+ Z(x_i,y_i,z_i)Δz_i

Поэтому

В случае замкнутой кривой L, т.е. когда M=N, криволинейный интеграл обозначают и назавают циркуляцией векторного поля F по замкнутому контуру L

2)

Ряд вида

называется функциональным. Областью сходимости этого ряда называется множество всех чисел при которых числовой ряд сходится.

Функциональный ряд вида

называется степенным рядом.

Теорема Абеля. Если ряд (1) сходится при некотором значении , то он сходится абсолютно при любом значении таком, что . Если же ряд (1) расходится при , то он расходится при любом модуль которого больше чем .

Следствие. Существует число или такое, что степенной ряд (1) сходится абсолютно при и расходится при .

Число R, о существовании которого говорится в следствии, называется радиусом сходимости степенного ряда (1).

Радиус сходимости можно вычислить по одной из следующих двух формул (при условии, что пределы существуют)

Определение 1. Если ряд (1) сходится к функции f(x) в окрестности точки a, то функцию называют аналитической в этой точке. Аналитичность функции на множестве означает аналитичность в каждой точке этого множества.

Билет 3