45Векторный потенциал магнитного поля

Векторный потенциал магнитного поля – это векторная величина, плавно изменяющаяся от точки к точке, ротор которой равен магнитной индукции

(17.13)

Основанием для представления индукции в виде ротора от вектора-потенциала служит то, что дивергенция любого ротора тождественно равна нулю, т.е.

Если вектор-потенциал как функция координат известен, то индукцию в любой точке поля определяют путем нахождения ротора от вектора-потенциала в соответствии с (17.13). Векторным потенциалом можно пользоваться и для областей, занятых током.

Векторный потенциал в произвольной точке поля связан с плотностью тока в этой же точке уравнением Пуассона.

Умножим обе части (17.6) на _a. Если магнитная проницаемость постоянна, то ее можно внести под знак ротора:

(17.14)

rot rot A = [V[VA]] = grad div A - V²A = m_ad

Так как есть расчетная функция, то в магнитном поле постоянного тока ее можно подчинить требованию:

(17.15)

Это требование означает, что линии вектора есть замкнутые сами на себя линии.

(17.16)

Уравнение (17.16) представляет собой уравнение Пуассона. В отличие от уравнения (13.21), составленного относительно скалярной величины , уравнение (17.16) составлено относительно векторной величины . Общее решение по аналогии может быть записано:

(17.17)

Единицей измерения является Вс/м. Формула (17.17) дает общее решение уравнения (17.16). Вектор в любой точке поля можно определить вычислением объемного интеграла (17.17). Последний должен быть взят по всем областям, занятым током. Следует отметить, что взятие интеграла правой части формулы (17.17) сопряжено обычно со значительными математическими выкладками.

Выражение магнитного потока через циркуляцию вектора-потенциала

Магнитный поток, пронизывающий какую-либо поверхность:

(17.7)

На основании теоремы Стокса поверхностный интеграл может быть преобразован в линейный

(17.18)

Для определения магнитного потока, пронизывающего некоторую площадь (поверхность) s, необходимо подсчитать циркуляцию вектора потенциала по замкнутому контуру, на который опирается поверхность s.

Определение потока по (17.18) часто имеет преимущества по сравнению с определением потока через магнитную индукцию (17.7). Соотношением (17.7) можно пользоваться в том случае, когда известно значение в любой точке поверхности s, тогда как для вычисления потока с помощью соотношения (17.18) достаточно знать значение на контуре и не требуется значения в точках внутри контура.

Рассмотрим граничные условия для векторного потенциала.

(17.19)

46. Расчет магнитного поля одиночного проводника с током

Требуется рассчитать магнитное поле внутри и за пределами проводника. Это означает, что необходимо определить распределение напряженности и вектора-потенциала.

Для расчета используем закон полного тока в интегральной форме

Рассчитаем циркуляцию вдоль окружности, центр которой совпадает с центром провода. При этом напряженность в любой точке этой окружности постоянна по модулю и совпадает с направлением элементарного участка dl.

Внутри проводника ( ) .

Следовательно,

Вне проводника ( ) .

Рассчитаем вектор-потенциал внутри проводника ( ). Так как по проводнику протекает ток, то вектор-потенциал подчиняется уравнению Пуассона .

Вектор-потенциал образует плоско параллельное поле, изменяющееся только по радиусу. Поэтому в цилиндрической системе координат уравнение Пуассона запишется

(17.20)

Проинтегрировав его, получим

(17.21)*

Так как поблизости нет другого поля, то постоянную интегрирования C₁ можно приравнять к нулю.

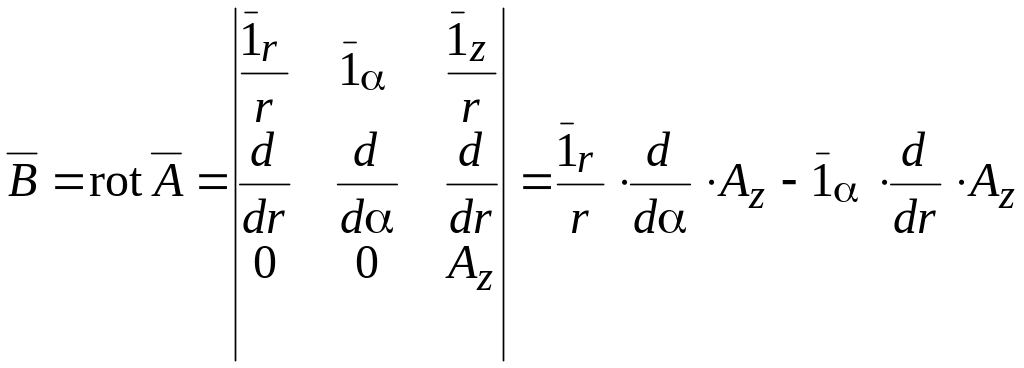
В свою очередь

(17.22)

При r = 0 , следовательно, и .

Проинтегрировав уравнение (17.21)*, получим

(17.23)

Если принять, что на поверхности проводника A₁ = 0, то постоянная интегрирования C₂ будет равна

Тогда

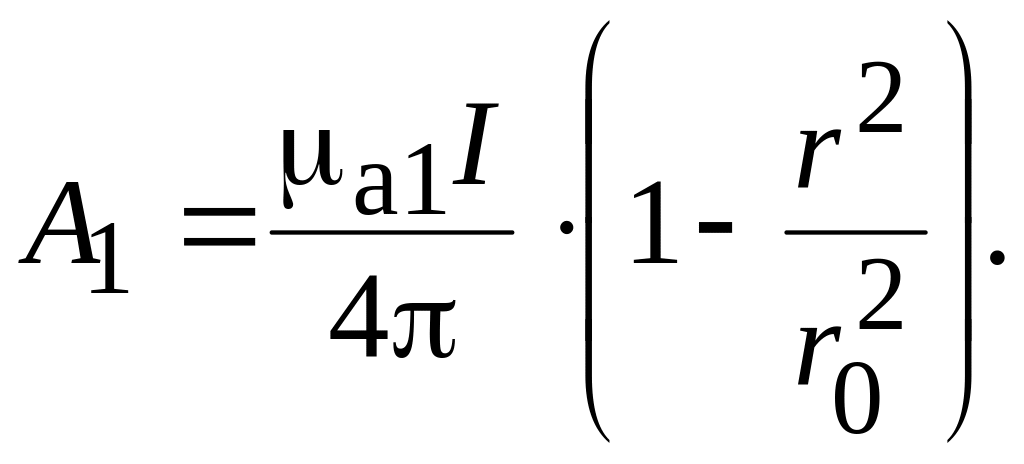(17.24)

Так как за пределами проводника тока нет, то вектор-потенциал подчиняется уравнению Лапласа .

Используя то же допущение о плоско параллельном поле, получим

(17.25)

На поверхности провода по закону полного тока

(17.26)

Следовательно,

(17.27)

(17.28)

Из условия непрерывности вектора-потенциала следует, что при A₂ = A₁ = 0.

(17.29)

Тогда

(17.30)

Выделим в толще проводника элементарную площадку, нормаль к которой параллельна вектору напряженности.

По теореме Стокса

(17.31)

Этот интеграл распадается на 4 составляющие

На участках 2-3 и 4-1 векторы и перпендикулярны, поэтому их скалярное произведение равно нулю.

Индуктивность, обусловленная магнитным потоком внутри проводника

(17.32)

В свою очередь

(17.33)

Тогда

(17.34)

(17.35)

За пределами проводника ( )

(17.36)