1. Всегда параметры электрической цепи в той или иной степени распределены вдоль ее участков, и только абстрагируясь от действительности можно предполагать, что такие параметры цепи как активное сопротивление – R, индуктивность – L и емкость – C сосредоточены в ее определенных участках. Во многих случаях такое допущение не приводит к существенным ошибкам в результатах проводимого анализа. Ранее мы имели дело с цепями с сосредоточенными параметрами.

Критерием необходимости рассматривать цепь в качестве цепи с распределенными параметрами является то, что интервал времени распространения электромагнитной волны вдоль всей цепи и интервал времени, в течение которого токи и напряжения меняются на заметную величину, должны быть соизмеримыми.

Токи напряжения в таких цепях являются функциями двух независимых переменных: времени – t и расстояния – x, отсчитываемого вдоль направления цепи. Уравнения, описывающие процессы в таких цепях, являются уравнениями в частных производных. Примерами являются линии передачи электрической энергии, линии связи, антенные вводы радиотехнических устройств, обмотки электрических машин при воздействии на них импульсных токов и напряжений.

Параметры цепи могут быть распределены неравномерно вдоль линии. Однако во многих случаях этим можно пренебречь и считать параметры равномерно распределенными. Такие линии называются однородными.

В дальнейшем под величинами R, L, C, G, M будем понимать активное сопротивление, индуктивность и т.д., приходящиеся на единицу длины, и будем обозначать их через R₀, L₀, C₀, G₀, M₀. В общем случае эти параметры зависят от частоты, например, увеличение активного сопротивления и индуктивности с ростом частоты вследствие поверхностного эффекта. Однако для простоты в дальнейшем это учитывать не будем.

Уравнения однородной линии с распределенными параметрами

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i(x, t) и напряжения между проводами u(x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо называется "началом" левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x'. Вся длина линии l = x + x'.

Пользуясь первичными параметрами R₀, L₀, C₀, G₀ нарисуем участок x в виде схемы замещения (рис)

Обозначим:

u – напряжение между верхним и нижним проводом в точке x;

u – приращение напряжения на участке x;

i – ток в точке x;

i – приращение тока на участке x.

Уравнения для приращений напряжения и тока на элементе x линии запишутся:

(13.1)

Это уравнение в частных производных. По мере стремления x к нулю степень точности этих уравнений повышается, причем величина второго порядка малости в правой части второго уравнения может быть опущена.

В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений на x и перейдя к пределу x  0, получим дифференциальные уравнения линии

(13.2)

Эти уравнения носят название телеграфных.

Если за начало отсчета принять конец линии, т.е. ввести координату x', уравнения примут вид:

(13.3)

Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.

2. Расстояние между двумя ближайшими точками, взятое в направлении распространения волны, фазы колебаний напряжения различаются на 2, называется длиной волны – 

,

. (13.13)

С течением времени волна перемещается от начала линии к ее концу. Она называется прямой или падающей волной.

Скорость перемещения падающей волны вдоль линии называется фазовой скоростью. Она определяется как скорость перемещения точки, фаза колебаний которой остается постоянной. Для прямой волны это условие записывается в виде

Следовательно:

(13.14)

Аналогичное исследование второго слагаемого выражения (13.12) показывает, что для произвольного момента времени она представляет синусоидальную волну, амплитуда которой возрастает с увеличением х, т.е. по мере удаления от начала линии к ее концу. С течением времени волна перемещается от конца линии к ее началу. Эта волна называется обратной или отраженной волной (рис. 13.3). Фазовая скорость обратной волны .

3. Уравнения однородной линии в гиперболических функциях

Подставив значения постоянных интегрирования в уравнения для напряжения и тока получим:

(13.17)

Сгруппируем члены, включающие ток и напряжение

.; . (13.18)

Эти уравнения не содержат в явном виде прямые и обратные волны, так как их составляющие кусочно вошли в гиперболические функции.

Если известны параметры нагрузки, то удобнее расстояние отсчитывать от конца линии x = l – x':

; ;

где

Постоянные интегрирования и находятся в зависимости от напряжения и тока в конце линии (граничные условия), если они заданы. При

Откуда

Следовательно

(13.20)

Сгруппируем члены, включающие ток и напряжение

; .

4. Вторичные параметры линии

Распределение тока и напряжения вдоль линии зависит от коэффициента распространения волны и волнового сопротивления, которые называются вторичными параметрами

где – продольное сопротивление, – поперечная проводимость.

Рассмотрим зависимость вторичных параметров от частоты. При  = 0

т.е. коэффициент распространения и волновое сопротивление являются чисто активными величинами. С ростом частоты коэффициент затухания и коэффициент фазы монотонно увеличиваются. Причем если перейти к пределу , то обнаружится, что коэффициент затухания стремится к величине

а коэффициент фазы асимптотически приближается к прямой .

Так как обычно в линиях , то волновое сопротивление с ростом частоты уменьшается, стремясь к пределу .

Зависимости вторичных параметров линии от частоты показаны на рис. 13.4.

Рис. 13.4. Частотные характеристики вторичных параметров

Частотные характеристики говорят о том, что вследствие зависимости коэффициентов затухания и фазы от частоты сигнал сложной формы, проходя по линии, искажается.

Входное сопротивление линии

Под входным сопротивлением линии Z_вх понимают сопротивление двухполюсника, которым можно заменить линию с нагрузкой при расчете режима в начале линии

.

Согласно закону Ома – сопротивление нагрузки.

Тогда (13.22)

Входное сопротивление зависит от вторичных параметров и длины линии. При l = 0 , а при .

Входное сопротивление при любом сопротивлении нагрузки Z_н можно выразить через входные сопротивления линии при холостом ходе Z_x и коротком замыкании Z_к.

При холостом ходе

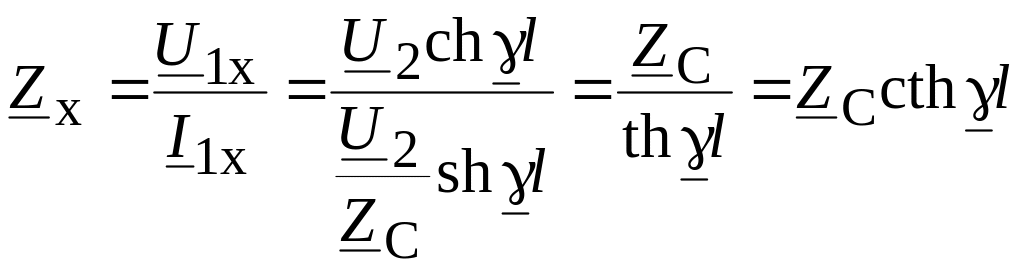. (13.23)

При коротком замыкании

. (13.24)

Вынесем в выражении (13.22) за знак скобки знаменателя

(13.25)

Из опытов холостого хода и короткого замыкания легко можно получить вторичные параметры

(13.26)

5. Связь вторичных параметров линии с сопротивлением х.Х. И к.З.

Входное сопротивление при любом сопротивлении нагрузки Z_н можно выразить через входные сопротивления линии при холостом ходе Z_x и коротком замыкании Z_к.

При холостом ходе

. (13.23)

При коротком замыкании

. (13.24)

Вынесем в выражении (13.22) за знак скобки знаменателя

(13.25)

Из опытов холостого хода и короткого замыкания легко можно получить вторичные параметры

(13.26)

6. Введем понятие коэффициента отражения волны

(13.27)

где – сопротивление нагрузки.

Отражение может возникнуть не только в конце линии, но и при подключении нагрузки в какой-либо ее точке. При этом

(11.28)

С учетом вышесказанного запишем уравнения линии в режиме несогласованной нагрузки, т.е. когда

(13.29)

или

(13.30)

В режиме холостого хода и . При коротком замыкании и . То есть коэффициент отражения изменяется в пределах от –1 до 1 и большее по модулю значение иметь не может.

В режиме холостого хода в любой точке линии согласно (13.21) имеем

.

При коротком замыкании

С учетом этих выражений систему (13.21) можно переписать в виде

(13.31)

Таким образом, режим несогласованной нагрузки характеризуется наличием двух волн. Энергия, приносимая прямой волной, частично поглощается нагрузкой, а частично возвращается к источнику.

Аналогично можно показать, что, если источник несогласован с линией, то часть обратной волны отражается от начала линии, и в линии возникает режим многократных отражений.

Входное сопротивление линии при несогласованной нагрузке (13.22):

7.

8. Режим согласованной нагрузки возникает, когда . При этом – , т.е. и обратная волна не возникает

Следовательно, вся энергия, поступающая с прямой волной, поглощается нагрузкой.

Из последних уравнений видно, что отношение напряжения к току в любой точке линии равно волновому сопротивлению

(13.32)

В частности, входное сопротивление

т.е. входное сопротивление линии равно волновому и не зависит от длины линии.

С учетом коэффициента распространения ток и напряжение в любой точке линии будут равны:

(13.33)

Их модули и вдоль линии изменяются по экспоненциальному закону, убывая от начала линии к ее концу (рис. 13.5).

В начале линии

Откуда

Выразим показатель степени l через токи и напряжения в начале и конце линии

; ; . (13.34)

Найдем КПД передачи энергии по линии

;

;

;

.

Тогда

(13.35)

Следовательно, даже в согласованной линии КПД передачи не равен единице. Он зависит от длины линии и от величины потерь, которые состоят из потерь в сопротивлениях проводов и в проводимости изоляции.

Мощность, передаваемая по согласованной линии, называется естественной или натуральной.