
- •1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(X) и ее производные .
- •2.Порядком дифференциального уравнения называется порядок нyивысшей производной, входящей в уравнение:
- •10.Если правая часть f(X) имеет вид: , где Pn(X)–многочлен n–ой степени; Qm(X)-многочлен m–ой степени.
- •Признак Лейбница.
1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(X) и ее производные .
Символически
дифференциальное уравнение выглядит:
F(x,y,y’,y’’…,y(n))=0
или
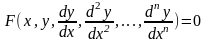 .
.
ДУ
n-го
порядка , если имеет решение, то его
можно записать:
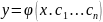 .
Это решение наз. общим решением, если
искомая фун. явно отражается от аргумента
х и consty.
Если решение получено в неявном виде
.
Это решение наз. общим решением, если
искомая фун. явно отражается от аргумента
х и consty.
Если решение получено в неявном виде
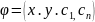 его наз. общим интегралом. Частным
решением интеграла диф. уравн. н-гопонрядка
называется такое его решение, в котором
произвольным константам Сi присвоены
конкретные значения.это конкретные
значения находятся из решения системы
так называемых начальных условий что
при х=х0 функция принимает значение
у=у0.Задача с начальными условиями и
постановками F(
x,y,
его наз. общим интегралом. Частным
решением интеграла диф. уравн. н-гопонрядка
называется такое его решение, в котором
произвольным константам Сi присвоены
конкретные значения.это конкретные
значения находятся из решения системы
так называемых начальных условий что
при х=х0 функция принимает значение
у=у0.Задача с начальными условиями и
постановками F(
x,y,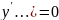 ,
y(
,
y(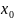 )=
)=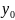 и
и
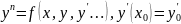 наз. задачи Коши.
наз. задачи Коши.
2.Порядком дифференциального уравнения называется порядок нyивысшей производной, входящей в уравнение:
Пример.
F(x,y,y’)=0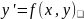 дифференциальное уравнение первого
порядка.
дифференциальное уравнение первого
порядка.
Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.
Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество
Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.
Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: у=у0 при х=х0
Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.
Тогда
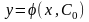 является частным решением уравнения.
является частным решением уравнения.
Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.
Если
в дифференциальном уравнении y=f(x,y)
функция f(x,y)
и ее частная производная
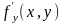 определены и непрерывны в некоторой
области Д на плоскости ХОУ, то какова
бы ни была внутренняя точка (х0,у0) этой
области, данное уравнение имеет
единственное решение
определены и непрерывны в некоторой
области Д на плоскости ХОУ, то какова
бы ни была внутренняя точка (х0,у0) этой
области, данное уравнение имеет
единственное решение
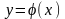 ,
удовлетворяющее начальному условию
у=у0 при х=х0.
,
удовлетворяющее начальному условию
у=у0 при х=х0.
3. Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
-
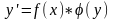 -
через производную.
-
через производную.
-
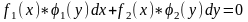 -
через дифференциал.В этих уравнениях
в произведениях стоят функции, каждая
из которых зависит от одной переменной
(х или у). Т.е. уравнение будет уравнением
с разделяющимися переменными, если его
можно преобразовать так, чтобы в одной
его части была только одна переменная,
а в другой – только другая.
-
через дифференциал.В этих уравнениях
в произведениях стоят функции, каждая
из которых зависит от одной переменной
(х или у). Т.е. уравнение будет уравнением
с разделяющимися переменными, если его
можно преобразовать так, чтобы в одной
его части была только одна переменная,
а в другой – только другая.
Уравнению f(y)=0 можно давать особые решения, т.е. те, кот.не входят в общее решение
4.
Функция f(x,y)
называется однородной функцией n–го
измерения, если при любом
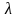 выполняется условие:
выполняется условие:
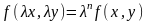
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy;
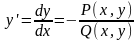
Однородное
уравнение всегда можно привести к виду
 и с помощью замены
и с помощью замены
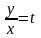 однородное уравнение всегда приводится
к уравнению с разделяющимися переменными
(
;
y=xt;
y’=t+xt’).
однородное уравнение всегда приводится
к уравнению с разделяющимися переменными
(
;
y=xt;
y’=t+xt’).
5.ДУ
наз. линейными, если входящая в него
фун.,производная, его диф-лы имеют только
1-ую степень, отсутствие их произведения
или фун. и ее производных не явл.
Аргументами др. фун.
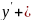 P(x)y=f(x).
P(x)y=f(x).
Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’
U’V+UV’+P(x)UV=Q(x)
V(U’+P(x)U)+UV’=Q(x)
Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными.
УБ- дифференциальные уравнения вида y’+P(x)y=Q(x)*yn, где
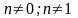 -
т.к. при этих значениях уравнение будет
линейным.
-
т.к. при этих значениях уравнение будет
линейным.
УБ решаются так же, как и линейные.
6.Уравнение
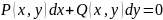
наз. уравнением полногодиф-ла, если сущ. диф-аяфун. U(x,y) для кот.левая часть уравнения явл. полным диф-лом.
du=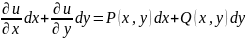 при
любых xи yиз
области определ. фун. Тогда u(x,y)=C.
при
любых xи yиз
области определ. фун. Тогда u(x,y)=C.
Необходимым и достаточным условием, того ,что уравнение будет уравнением в полных дифференциалах, выполнение равенства
dP/dy=dQ/dx
Ф-июU
можно начать восстан. по частям произв.
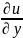
U=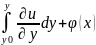
U(x,y)=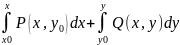
7.Определение. Дифференциальным уравнением n -го порядка
называется уравнение вида
F(x, y, y′,...,y(n) )= 0 или y(n) = f (x, y, y′,..., y(n−1) ).
Решением такого уравнения называется n раз дифференцируемая
функция y =ϕ (x), определенная на интервале (a,b), которая при подстановке
в уравнениях обращает его в тождество, т.е.
F(x,ϕ (x),ϕ′(x),...,ϕ (n)(x))≡ 0 или ϕ (n )(x) ≡ f (x,ϕ (x),ϕ′(x),...,ϕ (n−1)(x)).
При решении конкрет. физ. и др. задач чтобы получить частное решение
задают
дополнительные условия, например,
начальные условия. x =
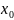 ,
y=
,
y=
1. Случай непосредственного интегрирования.
F(x,y”)=0
y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.
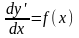 ;
;
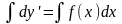 ;
;
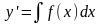 ;
;
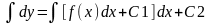
2. Когда дифференциальное уравнение явно не содержит у, т.е. F(x,y’,y”)=0
С
помощью замены у’=р;
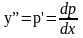 это уравнение приводим к уравнению
первого порядка
это уравнение приводим к уравнению
первого порядка
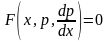 .
.
3. Когда дифференциальное уравнение явно не содержит х, т.е. F(y,y’,y”)=0.
С
помощью замены y’=p,
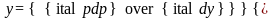 это уравнение приводим к уравнению
первого порядка
это уравнение приводим к уравнению
первого порядка
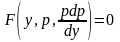 .
.
8.
Уравнение вида
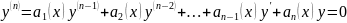
наз.
Линейным однородным диф-ым уравнением.
Если
 ,
f(x) непрерывны
в обл. Д, кот. Представляет собой интервал
(а,b), то верна теорема
Коши существования и единственности
решения любых уравнений предыдущего
вида. Для начальных условий y(
)=
,
,
f(x) непрерывны
в обл. Д, кот. Представляет собой интервал
(а,b), то верна теорема
Коши существования и единственности
решения любых уравнений предыдущего
вида. Для начальных условий y(
)=
,
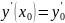
где
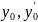 любые числа.
любые числа.
Составим характеристическое уравнение:
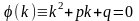 ,
которое получается из данного уравнения
путем замены в нем производных искомой
функции соответствующими степенями
“к”. Причем сама функция заменяется
единицей.
,
которое получается из данного уравнения
путем замены в нем производных искомой
функции соответствующими степенями
“к”. Причем сама функция заменяется
единицей.
Если к1 и к2 – корни характериситического уравнения, то общее решение однородного уравнения имеет один из следующих трех видов:
1).
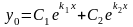 ,
если к1 и к2 – действительные и различные,
т.е.
,
если к1 и к2 – действительные и различные,
т.е.
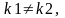 D>0.
D>0.
2).
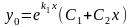 ,
если к1 и к2 – действительные и равные,
т.е. к1=к2, D=0.
,
если к1 и к2 – действительные и равные,
т.е. к1=к2, D=0.
3).
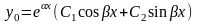 ,
если к1 и к2 – комплексные, т.е.
,
если к1 и к2 – комплексные, т.е.
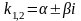 ;
D<0.
;
D<0.
9. Уравнение
вида
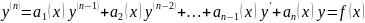 заданные в некоторой области Д функции,
наз. линейным неоднородным диф-ым
уравнением n-го порядка.Общее
решение имеет вид:
заданные в некоторой области Д функции,
наз. линейным неоднородным диф-ым
уравнением n-го порядка.Общее
решение имеет вид: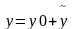 ,
где
,
где
y0
- общее решение соответствующегооднородного
уравнения;
 -
частное решение соответствующего
однородного уравнения.
-
частное решение соответствующего
однородного уравнения.
Т.е. для нахождения общего решения неоднородного уравнения ‘у’, сначала находят общее решение соответствующего однородного уравнения у0, а затем частное решение , и складывают их.
Частное
решение неоднородного уравнения
находится методом неопределенных
коэффициентов.Если ,
то
,
то
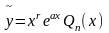 ,
где r– кратность корня
‘а’ в характеристическом уравнении,
т.е. r=0, если ‘а’ не есть
корень; r=1, если ‘а’
совпадает с одним из корней; r=2,
если ‘а’ совпадает с двумя корнями.
,
где r– кратность корня
‘а’ в характеристическом уравнении,
т.е. r=0, если ‘а’ не есть
корень; r=1, если ‘а’
совпадает с одним из корней; r=2,
если ‘а’ совпадает с двумя корнями.
