Вопрос13

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей и заданных общими уравнениями:

(4.23)

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей Следовательно, если плоскости (4.23) параллельны или совпадают, то т.е. существует такое число что

и наоборот.

Плоскости совпадают, если помимо этих условий справедливо Тогда первое уравнение в (4.23) имеет вид т.е. равносильно второму, поскольку

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число что но Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: и

Условия параллельности и совпадения плоскостей (4.23) можно записать в виде

Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):

или

Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

(4.25)

При этом условии система уравнений

имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина угла между двумя плоскостями удовлетворяет условию

Если — нормали к плоскостям и соответственно (рис.4.20,а), то величина угла между этими плоскостями вычисляется по формуле:

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.

При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина двугранного угла удовлетворяет условию

По формуле

(4.26)

получаем острый двугранный угол , образованный плоскостями (4.23), если (рис.4.20,а), и тупой в противном случае: (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.

Вопрос 14 Канонические и параметрические уравнения прямой

Поставим следующую задачу:

Составить уравнения прямой, проходящей через данную точку M(x0, y0, z0) параллельно данному вектору

→

a

= {l, m, n} ≠

→

0

(вектор

→

a

называется направляющим вектором прямой).

Решение. Пусть N(x, y, z) — произвольная точка пространства. Построим вектор MN = {x − x₀, y − y₀, z − z₀} (рис.1).

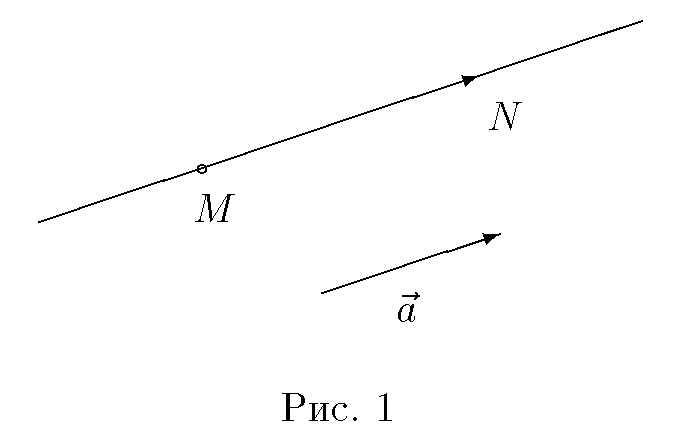
Очевидно, что точка N принадлежит прямой тогда и только тогда, когда вектор MN коллинеарен вектору

→

a

= {l, m, n} , т.е. когда их координаты пропорциональны:

x − x0 l = y − y0 m = z − z0 n

(1)

Эти уравнения называются каноническими уравнениями прямой в пространстве.

Замечания.

1. От канонических уравнений легко перейти к общим уравнениям прямой, например:

	      	x − x0 l = y − y0 m y − y0 m = z − z0 n

2. Одна или две координаты направляющего вектора прямой

→

a

могут быть равны нулю, это означает, что числитель соответствующей дроби тоже равен нулю.

Если в (1) ввести параметр t

x − x0 l = y − y0 m = z − z0 n = t,

то уравнения прямой можно записать в виде

	    	x = x0 + l·t y = y0 + m·t z = z0 + n·t

Эти уравнения называются параметрическими уравнениями прямой. Они имеют механический смысл: если параметр t рассматривать как время, а x, y, z — как координаты материальной точки, то параметрические уравнения описывают равномерное прямолинейное движение точки со скоростью

→

v

= {l, m, n} , (x₀, y₀, z₀) —начальное положение точки (при t = 0 ).

