8 вопрос

Смешанным произведением трех векторов называется число

Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.

П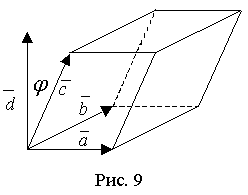 усть правая тройка векторов (рис. 9). Действительно, объем параллелепипеда, построенного на векторах , равен площади основания на высоту . Здесь φ - угол между векторами и

Знак смешанного произведения совпадает со знаком cos φ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.

Если перемножаемые векторы лежат в одной плоскости (cos φ = 0), то - необходимое и достаточное условие компланарности векторов.

Пусть векторы заданы своими разложениями по ортам в декартовой системе координат

Из 3.6.2 известно, что

Скалярно умножим этот вектор на вектор и, учитывая свойства скалярного произведения, получим

Это выражение может быть получено при вычислении определителя

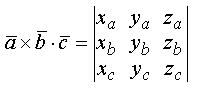
по элементам третьей строки, исходя из правила вычисления определителя.

Поэтому смешанное произведение трех векторов обозначают как , не подчеркивая при этом, какая пара векторов умножается векторно.

9 Вопрос

Линия на плоскости рассматривается (задается) как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, окружность радиуса R есть множество всех точек плоскости, удаленных на расстояние - R от некоторой фиксированной точки О (центра окружности).

Введение на плоскости системы координат позволяет определять по­ложение точки плоскости заданием двух чисел — ее координат, а положе­ние линии на плоскости определять с помощью уравнения (т. е. равенства, связывающего координаты точек линии).

Уравнением линии (или кривой) на плоскости Оху называется такое уравнение F(x;y) = 0 с двумя переменными, которому удовлетворяют координаты x и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Переменные x и у в уравнении линии называются текущими коорди­натами точек линии.

Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием его уравнения.

Так, для того чтобы установить лежит ли точка А(x₀; у₀) на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки А уравнению этой линии в выбран­ной системе координат.

Задача о нахождении точек пересечения двух линий, заданных урав­нениями F₁(x₁;y₁) = 0 и F₂(x₂;y} = 0, сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т. е. сводится к решению системы двух уравнений с двумя неизвестными:

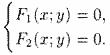
Если эта система не имеет действительных решений, то линии не пересекаются.

Аналогичным образом вводится понятие уравнения линии в полярной системе координат.

Уравнение F(r; φ)=О называется уравнением данной линии в поляр­ной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать при помощи двух уравнений:

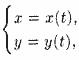где x и у — координаты произвольной точки М(х; у), лежащей на данной линии, а t — переменная, называемая параметром; параметр t определяет положение точки (х; у) на плоскости.

Например, если x = t + 1, у = t², то значению параметра t = 1 соот­ветствует на плоскости точка (3; 4), т. к. x = 1 + 1 = 3, у = 22 - 4.

Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линии называется параметрическим, а уравнения (10.1) — параметрическими уравнениями линии.

10 Вопрос

Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.

Если - полярный угол нормали, р - длина отрезка (рис.), то уравнение данной прямой может быть записано в виде

;

уравнение этого вида называется нормальным.

Пусть дана какая-нибудь прямая и произвольная точка ; обозначим через d расстояние от точки М* до данной прямой. Отклонением точки от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и -d, если данная точка и начало координат расположены по одну сторону от данной прямой. (Для точек, лежащих на самой прямой, =0). Если даны координаты , точки и нормальное уравнение прямой , то отклонение точки от этой прямой может быть вычислено по формуле

.

Таким образом, чтобы найти отклонение какой-нибудь точки от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки . Полученное число будет равно искомому отклонению.

Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: .

Если дано общее уравнение прямой , то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель , определяемый формулой

.

Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.