
Вступ
Координатний метод розв'язування задач на сьогоднішній день найбільш потужний і при правильному підході дозволяє розв'язувати фактично всі види математичних, фізичних, астрономічних і технічних задач.
ТЕЗИ
наукової роботи «Координатний метод розв'язування »,
виконаної
Гоменюком Владиславом Валентиновичем– учнем 9-Б класу
гімназії № 59 ім. О. М. Бойченка м. Києва, слухач МАН
педагогічний керівник: Кабанець Тетяна Іванівна –
вчитель-методист гімназії №59 ім.О.М.Бойченка
В своїй роботі я поставив задачу показати, як розв'язуються стереометричні задачі, якщо на них поглянути «по-іншому», тобто розглянути задачу в тривимірній системі координат.
Предметом дослідження є координатно-векторний метод розв’язування стереометричних задач.
Координатно-векторний метод розв’язування стереометричних задач
Деякі метричні задачі зручно розв’язувати за допомогою координатно-векторного методу. Це перш за все завдання, в яких мова йде про куб, прямокутний паралелепіпед або тетраедр з прямим кутом. Прямокутна система координат у просторі природним чином пов'язана з многогранниками, при цьому серед координат їх вершин є багато нулів, що спрощує обчислення.
Сутність координатного методу, як і векторного, полягає в тому, що геометрична задача перекладається на мову алгебри, і її розв’язання зводиться до розв’язання рівнянь, нерівностей чи їх систем.
З
курсу стереометрії відомо, що рівняння
площини, що проходить через точку ![]() перпендикулярно ненульовому вектору
перпендикулярно ненульовому вектору
![]() в прямокутній системі координат має
вигляд:
в прямокутній системі координат має
вигляд:
![]() ,
,
![]() ,
де
,
де ![]()
Навпаки,
будь-яке рівняння першого степеня ![]() визначає в координатному просторі єдину
площину, яка перпендикулярна вектору
з координатами (A,
B, C).
визначає в координатному просторі єдину
площину, яка перпендикулярна вектору
з координатами (A,
B, C).
Положення
площини в просторі однозначно визначається
заданням трьох точок, що не лежать на
одній прямій. Нехай дана площина перетинає
осі координат в точках ![]() ,
,
![]() ,
,
![]() ,
але не проходить через початок координат.
Підставивши координати цих точок у
загальне рівняння площини, отримаємо:
,
але не проходить через початок координат.
Підставивши координати цих точок у
загальне рівняння площини, отримаємо:
![]() ,
,
![]() ,
,
![]() ,
,
де
числа![]() відмінні від нуля. Звідси знаходимо:
відмінні від нуля. Звідси знаходимо:
![]()
і
рівняння ![]() приводиться до вигляду:
приводиться до вигляду:
![]()
Отримане рівняння називають рівнянням площини у відрізках. Його часто застосовують при розв’язуванні задач.
Як
відомо, відстань між двома точками ![]() і
і ![]() обчислюється за формулою:
обчислюється за формулою:
![]()
Користуючись даною формулою можна легко вивести рівняння сфери.
В
прямокутній системі координат рівняння
сфери радіуса R з центром в точці ![]() має вигляд:
має вигляд:
![]()
Якщо центр сфери співпадає з початком координат, то рівняння матиме вигляд:
![]()
Розглянемо способи задання прямої в координатному просторі.
Нехай
пряма l проходить через дану точку ![]() і паралельна ненульовому вектору
і паралельна ненульовому вектору ![]() Вектор
Вектор ![]() називають напрямним вектором прямої l
(рис. 2).
називають напрямним вектором прямої l
(рис. 2).
Довільна
точка ![]() належить прямій l тоді і тільки тоді,
коли вектори
належить прямій l тоді і тільки тоді,
коли вектори
![]() або
або ![]()
де t– деяке число (параметр). Дане співвідношення в координатах рівносильне системі рівнянь:

Дану систему називають параметричними рівняннями прямої.
Якщо
пряма l паралельна осі ![]() то вектор
то вектор ![]() є напрямним вектором, і рівняння прямої
прийме вигляд:
є напрямним вектором, і рівняння прямої
прийме вигляд: ![]()
![]() (координата z прийме довільне значення).
(координата z прийме довільне значення).
Нехай жодна з координат вектора не рівна 0. Тоді виключивши з отриманих рівнянь параметр t , отримаємо рівняння:
![]()
Отримані рівняння називаються канонічними рівняннями прямої.
Виведемо
формулу для обчислення відстані від
даної точки
до площини ![]() ,
заданої в прямокутній системі координат
рівнянням
,
заданої в прямокутній системі координат
рівнянням
![]()
Нехай
перпендикуляр, проведений з точки ![]() до площини
,
перетинає її в точці
до площини
,
перетинає її в точці ![]() (Рис.
3).
(Рис.
3).
Тоді
![]()
Так
як вектор ![]() перпендикулярний площині
і колінеарний вектору
перпендикулярний площині
і колінеарний вектору ![]() то згідно з визначенням скалярного
добутку,
то згідно з визначенням скалярного
добутку,
![]()
Позначимо
![]() Тоді
Тоді

Виразимо
скалярний добуток, що стоїть в знаменнику
дробу, через координати векторів ![]() і
Отримаємо:
і
Отримаємо:
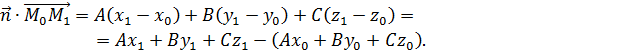
Точка
![]() лежить в площині
, тому
лежить в площині
, тому ![]() .
Таким чином, маємо:
.
Таким чином, маємо:
![]()
Враховуючи,
що ![]() ,
отримаємо:
,
отримаємо:

Отже,
для того щоб обчислити відстань від
точки ![]() до площини
,
потрібно в многочлен
до площини
,
потрібно в многочлен ![]() замість
замість ![]() підставити координати точки
,
взяти модуль отриманого числа і поділити
його на число
підставити координати точки
,
взяти модуль отриманого числа і поділити
його на число ![]()
Наведемо основні векторні співвідношення і формули, які використовуються для розв'язування стереометричних задач.
Для будь-яких трьох точок Α, Β,C має місце рівність:
![]() (правило трикутника).
(правило трикутника).
Для будь-яких трьох точок Α, Β і О виконується рівність:
![]() .
.
Для того, щоб точка С лежала на прямій АВ, необхідно і достатньо, щоб існувало таке число k, що
![]()
З даної рівності випливає, що
![]() .
.
Нехай А і В – дві різні точки прямої і точка С – точка даної прямої така, що
 .
Доведемо істинність формули:
.
Доведемо істинність формули:

де О – довільна точка.
Відмітимо,
що ![]() ,
інакше було б, що
,
інакше було б, що ![]() ,
або
,
або
![]() ,
,
тобто
![]() .
Але це неможливо, тому що А і В різні
точки.
.
Але це неможливо, тому що А і В різні
точки.
Нехай
або ![]() Користуючись правилом віднімання
векторів, отримаємо:
Користуючись правилом віднімання
векторів, отримаємо:
![]() ,
,
![]() ,
,

Дану
формулу називають формулою ділення
відрізка в даному відношенні. Якщо С –
середина відрізка АВ, то ![]() і
і
![]() .
.
Чотирикутник ABCD є паралелограмом тоді і тільки тоді, коли виконується одна з наступних рівностей:
![]() ,
,
![]() ,
,
![]() ,
,
де O – довільна точка простру.
Якщо вектори і
 неколінеарні, то для будь-якого вектора
неколінеарні, то для будь-якого вектора
 ,
що лежить в одній площині з
і
,
існує єдина пара чисел x і y таких, що
,
що лежить в одній площині з
і
,
існує єдина пара чисел x і y таких, що
 .
.В просторі для кожного вектора
 існує єдиний розклад за трьома
некомпланарними векторами
,
,
:
існує єдиний розклад за трьома
некомпланарними векторами
,
,
:
![]()
(x, y, z – однозначно визначені числа).
Нехай точки А, В, С не лежать на одній прямій; тоді для того щоб точка D лежала в площині АВС, необхідно і достатньо, щоб існувала така пара чисел α і β, що
 .
.
При розв’язуванні різних геометричних задач на обчислення довжин відрізків і величин кутів, на доведення геометричних нерівностей ефективно використовувати скалярне множення векторів. Нагадаємо його основні властивості.
З визначення скалярного добутку слідує, що
![]() ,
,
тобто скалярний квадрат вектора рівний квадрату його довжини. Отже, для знаходження довжини відрізка AB може бути використана формула
![]() .
.
За
допомогою скалярного добутку двох
векторів можна знаходити довжину
відрізка, величину кута, отже, знаходити
відстані, площі та інші метричні
характеристики геометричних фігур. Для
доведення перпендикулярності прямих
і площин зручно користуватися ознакою
перпендикулярності двох ненульових
векторів:![]()
Для
знаходження довжини відрізка АВ векторним
способом в якості базисних вибирають
такі вектори, довжини яких і кути між
якими вже відомі. Потім записують розклад
вектора ![]() за базисними векторами і знаходять:
за базисними векторами і знаходять:
![]()
Якщо
в задачі потрібно знайти величину кута
![]() ,
то в якості базисних беруть вектори з
відомими відношеннями їх довжин і кутами
між ними. Потім
вибирають вектори
,
то в якості базисних беруть вектори з
відомими відношеннями їх довжин і кутами
між ними. Потім
вибирають вектори![]() на сторонах цього кута з початком в його
вершині і розкладають їх по базису,
після чого знаходять cos φ
за формулою
на сторонах цього кута з початком в його
вершині і розкладають їх по базису,
після чого знаходять cos φ
за формулою

Для будь-яких векторів і має місце нерівність
![]() .
.
Відрізки AB і CD перпендикулярні тоді і тільки тоді, коли
![]() .
.
Для будь-яких векторів і має місце формула:
![]()
Для успішного використання векторного методу, корисно знати деякі рівності, які часто використовуються для роз’язування задач.
Для будь-яких векторів , , виконується рівність:
![]() .
.
Для будь-яких трьох точок A, B і C:
![]() ,
,
теорема косинусів.
Для будь-яких чотирьох точок A, B, C, D:
![]() .
.
Вектори
![]() і
і ![]() в лівій частині представимо у вигляді
різниці двох векторів, відкладених від
точки A. Отримаємо:
в лівій частині представимо у вигляді
різниці двох векторів, відкладених від
точки A. Отримаємо:
 .
.
Доведена рівність є узагальненням рівності 6), яка випливає з неї при співпаданні точок D і A.
