
- •Дифференциальные и интегральные уравнения
- •§ 1 Общие понятия
- •§ 2 Дифференциальное уравнение 1-го порядка
- •2.5 Уравнение в полных дифференциалах
- •§ 3 Линейные обыкновенные дифференциальные уравнения
- •Лоду 2-го порядка
- •Теорема существования и единства для ду n-го порядка и систематизации ду
- •§4 Интеграция ду 2-го порядка с постоянными коэффициентами
- •1 Случай :
- •2 Случай :
- •§5 Линейное неоднородное дифференциальное уравнение (лнду) Структура общего решения лнду 2-го порядка :
- •Метод Лагранжа Вариации произвольных постоянных
- •Интегрирование лнду 2-го порядка и правой частью специального вида :
- •Интегрирование лнду п-го порядка (n постоянным коэффициентом и правой частью специального вида
- •§6 Системы дифференциального уравнения
- •Случай :
- •Случай :
- •§ 7 Понятие об устойчивости оду и систем оду Понятие о фразовом пространстве ду
- •Устойчивость по Ляпунову
- •Простейшие типы точек покоя
- •Случай :
- •Случай :
- •Случай :
- •§8 Уравнения в частных производных Основные понятия
- •Уравнение Лапласа
- •Линейные и Квазилинейные уравнения частных производных
- •§ 9 Интегрирование линейных уравнений при помощи степенных рядов
- •§ 10 Линейные дифференциальные уравнения 2-го порядка в частных произвольных
Теорема существования и единства для ду n-го порядка и систематизации ду
Теорема (3.5)
Существует единственное решения ДУ n-го порядка
= f (x, y, y’, y’’ , …
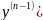
y ( ) =
y’ ( ) = ’
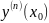 =
‘’ , … ,
(
)
=
=
‘’ , … ,
(
)
=
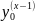
Если в
окрестности начальной точки :
(
,
,
’,
’’ ,
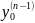 )
)
Функция f – является не прерывной функцией всех своих аргументов и удовлетворяющая условию Липшица по всем аргументам начиная со второго
Теорема (3.6)
Существование и единственности решения системы :
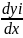 = f I ( x,
= f I ( x,
 )
)
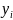 (
)
= y
I
0 (i=
1, 2, … , n)
(3.9)
(
)
= y
I
0 (i=
1, 2, … , n)
(3.9)
Предположим , что в области Д , определённое неравенством :
– a x + a i = (1, 2, … , )
– bi
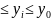 + bi
+ bi
Правые части уравнения (3.9) удовлетворяют условию :
①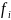 (x,
)
i= (1, 2, … , n)
│
│
M
(x,
)
i= (1, 2, … , n)
│
│
M
② все формулы (1 … n) удовлетворяет условия Липшица
│
(x, y,
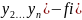 │
│
§4 Интеграция ду 2-го порядка с постоянными коэффициентами
Общий вид ДУ 2-го порядка с постоянными коэффициентами :
y’’ + py’ + ϕ y = 0 (4.1)
Интеграция ДУ 2-го порядка с носителем коэффициента
В частном случае в рассмотренным выше линейно однородном уравнение является ЛОДУ 2-го порядка.
Рассмотрим ЛОДУ 2-го порядка (и 1) где p и q = const
y
=
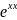 (Л. Эйлер)
(Л. Эйлер)
Подставим y = в уравнение (4.1)
y
‘=k
, y ‘’=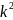
+ p ‘k + q = 0 (4.2)
+ pk +q = 0 (4.2 a)
Уравнение (4.2 а) называется Характеристическим для уравнения (4.1)
При решении (4.2 а) возможны 3 случая
1 Случай :
Корни в (4.2 а) действительны и различны
=
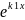 =
=
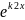 линейно не зависимые и образуют
фундаментальную систему уравнения
(4.1)
линейно не зависимые и образуют
фундаментальную систему уравнения
(4.1)
В этом случае общие решения записываются в виде :
y=

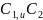 = const
= const
2 Случай :
Корни
действительны, но одинаковы
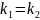
Дискриминант при этом = 0
В этом случае имеем 1 решение :
=
Покажем
, что
=
=

Покажем , что функция = , будет также решением уравнения (4.1)
’
=
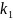 +
+
 =
(k1x + 1)
=
(k1x + 1)
’’
=
(
 x +
+
)
x +
+
)
y’’ + py’ + q y = 0 (4.1)
(
x +
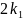 )
+ p
(k1x + 1) + q *
x = 0
)
+ p
(k1x + 1) + q *
x = 0
x
(
x
+
 +q)
+
+ p
= 0
+q)
+
+ p
= 0
Поскольку
дискриминант = 0
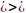 = -
= -
 =
является решением уравнения (4.1)
=
является решением уравнения (4.1)
Общее решение :
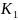 =
α
+
=
α
+
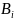
 =
α
-
=
α
-
Д 0
=
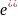
=
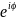 = cos ϕ + sin ϕ
= cos ϕ + sin ϕ
=
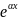 ( cos bx + I sin bx)
( cos bx + I sin bx)
= ( cos bx - I sin bx)
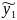 =
=
 =
cos px
=
cos px
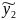 =
=
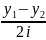 =
sin px
=
sin px
y = cos bx + sin bx
Пример 1 :
Решение
уравнения :
 ‘ + 25 y
= 0
‘ + 25 y
= 0
– 6k + 25 = 0
Д = 36 – 100 = -64
 =
=
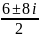 = 3
= 3
 4 i
4 i
Ответ
:
=
*
 cos 4x +
*
sin 4x
cos 4x +
*
sin 4x
Таким образом , чтобы решить уравнение (4.1) нужно решить характеристическое уравнение (4.2 а) и выписать решение без интегралов
Интегрирование ЛОДУ п –го порядка с постоянными коэффициентами
Задача нахождения общего решения ЛОДУ п – го порядка
(n 2)
С постоянный коэффициент :
+
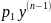 +
+
 + ….
+ ….
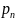 * y
= 0
* y
= 0
Где
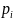 R
R
Решение аналогичного случая уравнения 2 – го порядка
Выписываем характеристическое уравнение
 +
+
 +
+
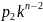 + ….
= 0 (4.5)
+ ….
= 0 (4.5)
и находим n-го числа его корней в том числе и комплексных :
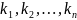
Ki = kj
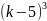 = 0
= 0
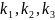 = 5
= 5
В этом
случае кратноcть
 = 3 (кратность корня)
= 3 (кратность корня)
Если
кратность
 = 1 , то Ki
называется простым
корнем
= 1 , то Ki
называется простым
корнем
Cлучай 1:
Все корни (4.5) действительны и различны
Общее решение :
y=
Пример 2 :
Найти общее решение уравнения :
y’’’- y’’’ – 4y’ + 4y = 0
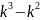 – 4k
+4 = 0
– 4k
+4 = 0
= 1
(k-1) – 4 (k-1) = 0
(k-1) ( -4) = 0
(k-1) (k-2) (k+2) = 0
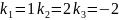
y
=
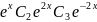
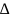
Случай 2:
Все корни действительны , но есть кратные ;
Тогда
корню K
кратности m
соответствует решение y
=
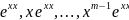
Случай 3 :
Среди корней есть комплексные сопряжённые
Тогда
каждой паре α
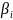 простых корней соответствует пара
решений :
простых корней соответствует пара
решений :
cos bx sin bx
cos bx ; x sin bx
sin bx , … ,
 sin bx
sin bx
