Математические выражения, описывающие волновые процессы

В связи с многообразием, нелинейностью свойств субстанции, особенностями границ и способов возбуждения, пользуются свойством разложения любых, самых сложных колебаний в спектр по частотам отклика субстанции на возбуждение. Для дискретных спектров наиболее общим решением моделирующих уравнений является выражение, которое удобно представлять в комплексной форме:

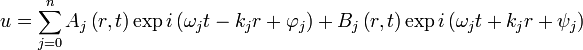
где j – номер моды, гармоники спектра; ψj φj – постоянные фазы запаздывания колебаний данной моды, определяемые, как правило, различием реакции динамической системы в точке её возбуждения, а также особенностями границ; они могут в общем случае иметь как действительный, так и комплексных вид; n – количество мод в спектре, которое может быть и бесконечным. Мода с j = 0 называется основной модой, гармоникой. С нею переносится самая большая часть энергии волнового процесса. Для интегральных спектров вместо сумм записываются интегралы по частотам спектра. В дискретных структурах имеют место три режима колебательного процесса: периодический, критический, и апериодический.

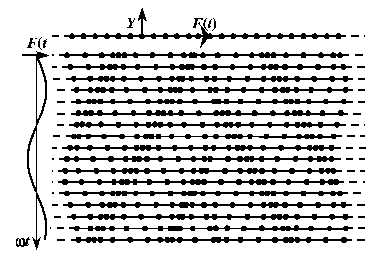
Периодический режим колебаний в бесконечной упругой линии с сосредоточенными параметрами.

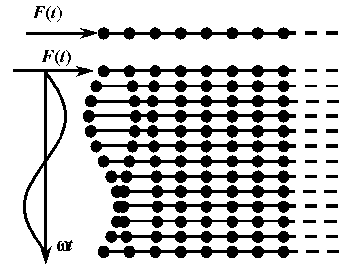
Апериодический режим колебаний в полубесконечной упругой линии с сосредоточенными параметрами.

В идеальной дискретной системе переход от одного режима к другому определяется разностью фаз колебания соседних элементов. При достижении противофазности колебаний система переходит от периодического режима к критическому. В апериодическом режиме противофазность колебаний соседних элементов сохраняется, но от точки возбуждения идёт интенсивное затухание колебательного процесса последующих элементов системы. Данный режим проявляется и в конечных упругих линиях:

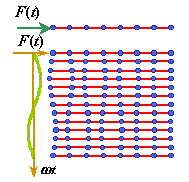
Характерный вид стоячей волны для апериодического режима в упругой линии со свободными концами.

В линиях с сопротивлением колебания соседних элементов никогда не достигают противофазности. Тем не менее, особенности колебаний, характерные для апериодического режима, сохраняются и при наличии сопротивления .

Гармоническая волна

Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения

где A – некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; ω = 2π / T = 2πf – круговая частота волнового процесса, T – период гармонической волны, f – частота; k = 2π / λ = ω / c – волновое число, λ – длина волны, c – скорость распространения волны; φ0 – начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.

Если искать решение для гармонической волны путём предельного перехода от соответствующих решений для динамических систем с сосредоточенными параметрами, то указанное выражение существенно уточнится, выявив связь, заложенную в амплитуду A. Это решение для амплитуды имеет вид

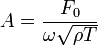
где, F0 – амплитуда воздействующей силы , ρ – плотность распределённой упругой системы, T – в данном случае, жёсткость линии с распределёнными параметрами .