Министерство образования и науки РФ

Федеральное ГБОУ ВПО

Тамбовский Государственный технический университет

Кафедра: «Архитектура и строительство зданий»

Расчетно-графическая работа по дисциплине «Информатика» на тему: «Системы счисления. Выполнение расчетов в позиционной системе счисления»

Вариант 5.

Выполнила:

студентка группы БСТ - 12

Деревякина В.Ю.

Преподаватель: Ляпина Е.Д.

ТАМБОВ 2011

Оглавление

Введение 1

Задание I. «Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления» 6

Задание II. «Перевести данное число в десятичную систему счисления» 8

Задание III. «Сложить числа» 9

Задание IV. «Выполнить вычитание» 10

Задание V. «Выполнить умножение» 11

Приложение……………………………………………………………………..12

Введение

Системой счисления называется совокупность правил для обозначения (записи) действительных чисел с помощью цифровых знаков. Для записи чисел в конкретных системах счисления используется некоторый конечный алфавит, состоящий из цифр а1 , а2, а3,….,аn. При этом каждой цифре аi в записи числа ставится в соответствие определенный количественный эквивалент.

Вычислительные машины в принципе могут быть построены в любой системе счисления. Но столь привычная для нас десятичная система окажется крайне неудобной. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент со множеством состояний (колесо с десятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях.

В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.

Непозиционные системы счисления

В ней количественный эквивалент каждой цифры, входящей в запись данного числа, не зависит от места (позиции) этой цифры в ряду других цифр. Пример: римская система счисления. В ней для записи различных целых чисел используются символы I, V, X, L, C, D, M и т.д., обозначающие соответственно 1, 5, 10, 50, 100, 500, 1000 и т.д. Например, запись MCMLXXXV означает число 1985. Общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа.

Позиционные системы счисления

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число - два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем.

Основные позиционные системы счисления

Десятичная система счисления

Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа - число десятков, следующая - число сотен и т.д. Позиции цифр в записи числа называют его разрядами. В десятичной системе счисления вес каждого разряда в 10 раз больше веса предыдущего. Всякое число в десятичной системе счисления можно представить в виде суммы различных целых степеней десяти с соответствующими коэффициентами аi (0-9), взятыми из алфавита данной системы счисления.

Например: 245,83 = 2 * 102 + 4 * 101 + 5 * 100 + 8 * 10-1 + 3 * 10-2. Любое десятичное позиционное число N можно представить с помощью целых степеней десяти, взятых с соответствующими коэффициентами, т.е.

N10 = am * 10m + am-1 * 10m-1 + …+ a1*10+ +a0 * 100 + a-1 * 10-1 +…+ a-n * 10-n.

Двоичная система счисления.

В этой системе всего две цифры - 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра - число двоек, следующая - число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число - представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Наиболее простыми с точки зрения технической реализации являются двухпозиционные элементы, например, электромагнитное реле, транзисторный ключ.

Восьмеричная система счисления.

В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает - как и в десятичном числе - просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.

Шестнадцатеричная система счисления.

Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем - 16 (десятичное), в следующем - 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.

Задание I. «Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления»

А) а) 530(10);

Для перевода числа в двоичную систему счисления воспользуемся методом поэтапного деления на основание системы счисления.

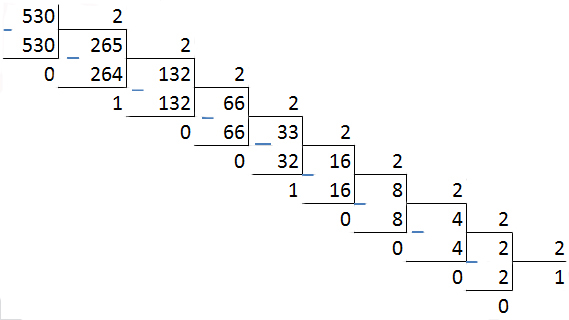
1. Исходное число делим на основание системы счисления с остатком в десятичной системе.

2. Если частное от деления не равно 0, выполняем п.1.

3. Полученные остатки записываем последовательно от последнего к первому.

4. Полученная запись - искомое двоичное число.

530(10) = 1000010010(2)

б) 530(10) = 001 000 010 010(2) = 1022 (8)

Для перевода числа из десятичной системы в восьмеричную используем метод разложения на триады и используя промежуточные системы счисления.

Для перевода из десятичной системы счисления в восьмеричную нужно воспользоваться промежуточной (двоичной) системой счисления. Далее двоичное число необходимо разбить на группы по три цифры(триады), начиная справа, и, если в последней группе окажется меньше трех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа(правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями. Далее необходимо триады заменить на восьмеричные числа, пользуясь таблицей 1(Приложение).

в) 530(10) = 001 000 010 010(2) = 212 (16)

Для перевода из десятичной системы счисления в шестнадцатеричную, воспользуемся разложением числа на тетрады.

Этот метод аналогичный предыдущему, отличающийся только тем, что в нем мы разбиваем число на группы по четыре цифры в каждой (тетрады) и так же пользуемся таблицей 1 (Приложение).

Примеры б-д переводятся в нужные системы счисления аналогично.

Б) 265(10) = 100001001(2)

265(10) = 411(8)

265(10) = 109(16)

В) 597,25(10) = 1001010101,01(2)

597,25(10) = 1125,2(8)

597,25(10) =255,4(16)

Г) 300,375(10) = 100101100,011(2)

300,375(10) = 454,3(8)

300,375(10) = 12С,6(16)

Д) 75,57(10) = 1001011,10010(2)

75,57(10) = 113,44(8)

75,57(10) = 4В,91(16)

Задание II. «Перевести данное число в десятичную систему счисления»

Для перевода в десятичную систему счисления используем метод разложения по базису системы счисления.

А) 101000111₍₂₎ = 1⁸0⁷1⁶0⁵0⁴0³1²1¹1⁰ = 1*2⁸+0*2⁷+1*2⁶+0*2⁵+0*2⁴+0*2³+1*2²+1*2¹+1*2⁰ = 256+64+4+2+1 = 327(10)

Алгоритм:

1. Пронумеровать разряды целой части числа справа налево, начиная с нуля по возрастанию, а дробной части числа слева направо, начиная с -1 по убыванию.

2. Записать число в развернутой форме, заменив все цифры и основание системы счисления десятичными эквивалентами.

3. Вычислить значение полученного выражения, выполнив действия в десятичной системе счисления

Примеры б-д решаются аналогично.

Б) 110001001₍₂₎ = 393₍₁₀₎

В) 1001101010,01₍₂₎ = 618,25₍₁₀₎

Г) 1011110100,01₍₂₎ = 756,25₍₁₀₎

Д) 1317,75₍₈₎ = 719,95₍₁₀₎

Е) 2F4,0C₍₁₆₎ ;

Схема Горнера. Запишем число в развернутой форме и преобразуем полученную сумму к эквивалентной скобочной форме:

2²F¹4⁰,0^-1C^-2 = 2*16²+F*16¹+4*16⁰, 0*16^-1+С*16^-2 = 512+240+4+0,05 = 756,05₍₁₀₎

Задание III. «Сложить числа»

А) 1100011010₍₂₎ +11101100₍₂₎ = 10000000110₍₂₎

1100011010

+0011101100

10000000110

Проверка :

1100011010₍₂₎ +11101100₍₂₎ = 794₍₁₀₎ + 236₍₁₀₎ = 1030₍₁₀₎ = 10000000110₍₂₎

Б) 10111010₍₂₎+1010110100₍₂₎ = 1101101110₍₂₎

0010111010

+1010110100

1101101110

Проверка:

186₍₁₀₎ + 692₍₁₀₎ = 878₍₁₀₎ = 1101101110₍₂₎

В) 1000110111,011₍₂₎+1110001111,001₍₂₎ = 10111000110,100₍₂₎

1000110111,011

+1110001111,001

10111000110,100

Проверка:

567,375₍₁₀₎ + 911,125₍₁₀₎ = 1478,500₍₁₀₎ = = 10111000110,100₍₂₎

Г) 1745,5₍₈₎+ 1473,2 ₍₈₎ = 3440,7₍₈₎

1745,5

+1473,2

3440,7

5+3 = 8=8+0

1+4+7 = 12=8+4

1+7+4 = 12 = 8+4

1+1+1=3

Проверка:

997,6₍₁₀₎ +827,3₍₁₀₎ = 1824,9₍₁₀₎ = 3440,7₍₈₎

Пример д) решается аналогично примеру г):

Д) 24D,5₍₁₆₎+141,4₍₁₆₎ =38E,9₍₁₆₎

Проверка:

589,3₍₁₀₎+321,3₍₁₀₎ = 910,6₍₁₀₎ = 38E,9₍₁₆₎

Задание IV. «Выполнить вычитание»

А) 1100101010(2) -110110010(2) = 101111000(2)

_1100101010

0110110010

101111000

Проверка:

810(10) – 434(10) = 376(10) = 101111000(2)

Б) 110110100(2) – 110010100(2) = 100000(2)

_110110100

110010100

100000

Проверка:

436(10) - 404(10) = 32(10) = 100000(2)

В) 1101111111,1(2) – 1100111110,1011(2) = 1000000,1101(2)

_1101111111,1000

1100111110,1011

1000000,1101

Проверка:

895,5(10) – 830,7(10) = 64,8(10) = 1000000,1101(2)

Г) 1431,26(8) – 1040,3(8) = 370,76(8)

_1431,26

1040,30

370,76

Проверка:

793,35(10) – 544,38(10) =248,97(10) = 370,76(8)

Д) 22C,6(16) – 54,2(16) = 1D8,4(16)

_22C,6

54,2

1D8,4

Проверка:

556,38(10) – 84,13(10) = 472,25(10) = 1D8,4(16)

Задание V. « Выполните умножение»

А)1001001(2) * 11001(2) = 11100100001(2)

1001001

* 11001

1001001

1001001

1001001

11100100001

Проверка:

73(10) * 25(10) = 1825(10) = 11100100001(2)

Б)245,04(8) * 112,2(8) = 27737,7100(8)

245,04

* 112,20

0

51210

51210

24504

24504

27737,7100

Проверка:

165,0625(10) * 74,25(10) = 12255,890625(10) = 27737,7100(8)

В) 4В,2(16) * 3С,3(16) = 11А9,96(16)

4В,2

*3С,3

Е16

3858

Е16

11А9,96

Проверка:

75,125(10) * 60,1875(10) = 4521,5859375(10) = 11А9,96(16)