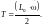Когда и где применяется эта теорема?
Максимальное количество уравнений, которые можно написать, основываясь на этой теореме, будет только одно.
Поэтому в силу простоты теоремы, ее целесообразно применять для описания динамики сколь угодно структурно сложных систем, имеющих всего одну степень свободы.
Итак, теорема об изменении кинетической энергии в дифференциальной форме применяется в том случае при решении задач, когда нужно:
1) Составить дифференциальное уравнение движения системы как целого с одной степенью свободы и находить S = S(t) и V = V(t).
2)Определить по известной кинетической энергии (в функции от времени) мощность и наоборот.
Интегральную форму применяем тогда, когда
1) нужно подсчитать работу, которая была совершена, по изменению кинетической энергии и наоборот;
2) необходимо решать задачи, связанные с выстрелами и ударами;
3) необходимо определять V = V(S) и V = V(j).
Для того чтобы применить эту теорему для решения задач, необходимо уметь вычислять кинетическую энергию системы и научиться вычислять работу и мощность для разных случаев движения.
Лекция 8
8.1. Вычисления кинетической энергии системы
Докажем фундаментальную теорему Кёнига (König, XIX век, Пруссия):
Кинетическую энергию системы можно представить как сумму кинетической энергии поступательного движения системы вместе с центром масс и кинетической энергии системы ее движения относительно центра масс.
,
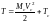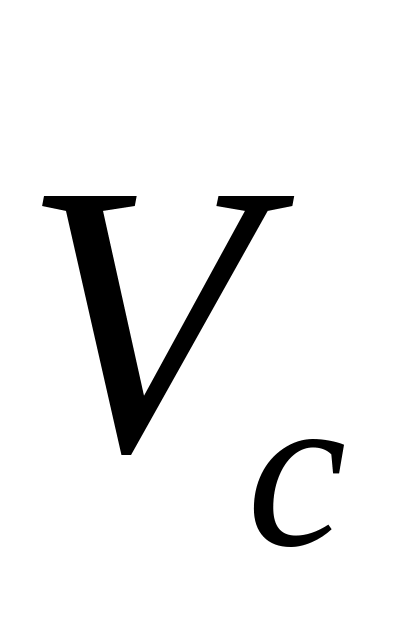
г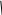
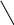
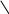
де
– кинетическая
энергия относительно центра масс (рис.
8.1).
Доказательство
Центр масс системы есть точка С.
Скорость
i-точки
представляется по теореме о сложении
скоростей как сумма двух
скоростей:
.
Тогда
.
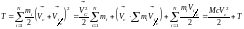Что
и требовалось доказать.
8.2. Кинетическая энергия тела при простейших его движениях
Известно, что существует пять простейших форм движения твердого тела: поступательное, вращательное, плоское, сферическое и произвольное.
1.
Тело движется
поступательно:
.
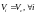Скорость любой
точки равна скорости полюса, в том числе
центра масс для всех
i. Воспользуемся
теоремой Кенига.
Так как
никакого относительного движения нет,
то сразу получаем
.
2. Вращение вокруг неподвижной оси
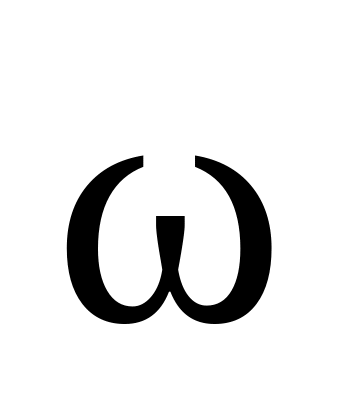
Н
аипростейший
способ определения Т
в этом случае будет такой. Берем какую-то
i-ю
точку тела. Эта точка движется по
окружности с центром С
на оси (рис. 8.2).
Скорость i-й точки подсчитывается по формуле Vi = ωdi.
Тогда кинетическая энергия будет равна
.
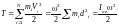Здесь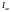
есть осевой
момент инерции.
Из физики напомним, что
Осевой момент инерции является мерой инертности тела при его вращательном движении вокруг оси и характеризует инертность тела через распределение масс относительно оси вращения.
3. Плоское движение твердого тела
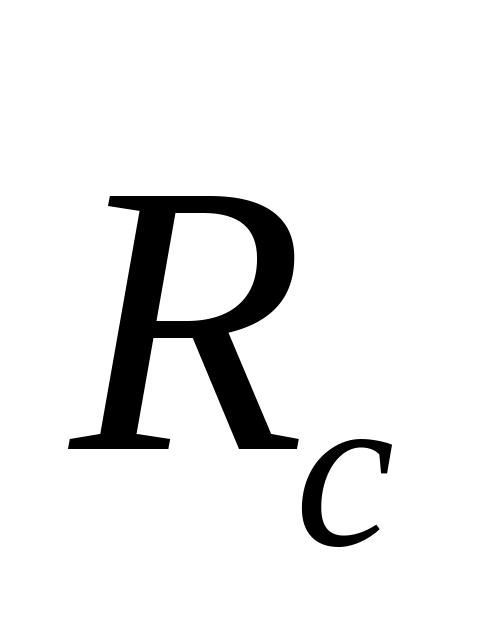
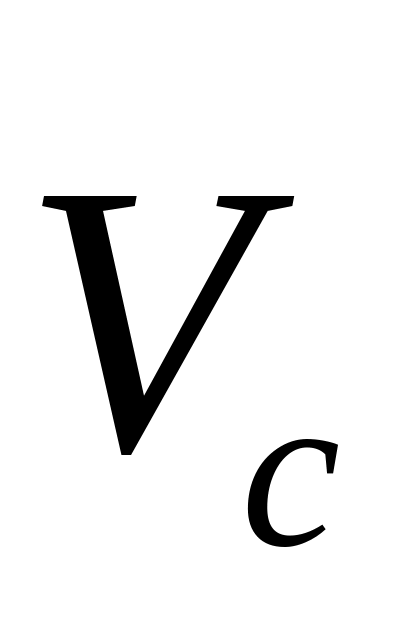
В
этом случае воспользуемся теоремой
Кёнига. Вспомним, что плоское
движение
твердого тела представляется всегда
как движение
его плоской фигуры (рис. 8.3).
Рис. 8.3
На
основании теоремы Кёнига сразу получим:
.
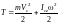4. Сферическое движение твердого тела
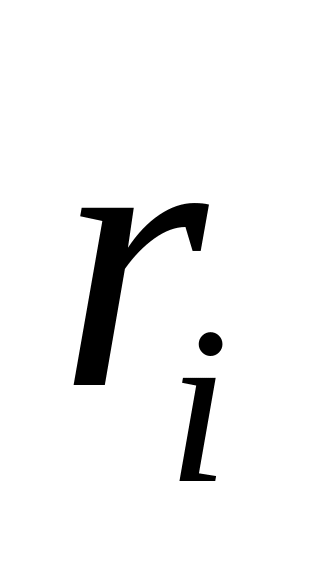
З
десь
твердое тело вращается вокруг неподвижной
точки О
(рис. 8.4).
Для подсчета кинетической энергии
воспользуемся тем, что кинетическая
энергия сферического движения может
быть вычислена по формуле для вращательного
движения вокруг мгновенной оси вращения
OL:
.
Что здесь плохо? Так как ось OL сама вращается, то момент инерции будет неизвестной функцией времени, что для расчета явно не годится.
Как
посчитать кинетическую энергию?
Перепишем выражение для кинетической
энергии
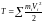в иной форме:
,
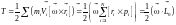где
,
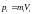а
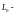кинетический
момент тела. Таким образом:
