2.Свойства двойственного графа плоского графа.

Д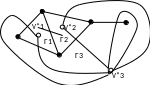 ля плоского графа G построим новый плоский граф G^*, который назовем геометрически двойственным к G. Для этого внутри каждой грани _i графа G выберем по одной точке v_i^*. Эти точки-вершины будущего графа G^*. Далее, каждому ребру e  EG поставим в соответствие жорданову кривую e^*, которая пересекает лишь одно ребро e графа G и соединяет вершины v_i^*, лежащие в гранях, границы которых содержат ребро e (таких граней может быть две или одна). Кривые e^* — ребра графа G^*. Очевидно, что ребра графа G^* можно провести так, чтобы они не пересекались.

Из этого построения очевидно, что граф G^*, геометрически двойственный к плоскому графу G, определяется однозначно с точностью до изоморфизма, причем граф G^* всегда связен. Последнее утверждение легко доказать индукцией по числу вершин графа G^* (т. е. по числу граней графа G) путем стягивания ребра e^* графа G^*, что, очевидно, соответствует удалению ребра в графе G. При этом, если ребро e — граница двух граней, то упомянутые операции приводят к уменьшению числа вершин графа G^* (числа граней графа G) на единицу.

Применяя формулу Эйлера, легко получить

Утверждение 13.18. Если G — плоский связный (n, m)-граф с f гранями, а G^* — (n^*, m^*)-граф, геометрически двойственный к нему, с f ^* гранями, то n^* = f , m^* = m и f ^* = n.

Теорема 13.19. Если G — плоский связный граф, то граф G^** изоморфен графу G.

 Из утверждения 13.16 следует, что n^** = f^* = n, где n^** = | G^**|. Следовательно, каждая грань графа G^* содержит одну вершину графа G (G^**). Поэтому построение, при помощи которого граф G^* получен из G, можно обратить, т. е. получить G из G^*. 