БИЛЕТ 16

1. Оценки хроматического числа. Теорема Брукса.

Поскольку задачу правильной раскраски точно решить трудно, то актуальны оценки хроматического числа, выражаемые в терминах более или менее просто вычислимых параметров графа. Рассмотрим несколько оценок хроматического числа, связанных со степенями вершин графа.

Обозначим через  множество всех порожденных подграфов графа G, а через 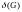, как обычно, — минимальную из степеней вершин графа .

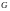Теорема 15.2. Для любого графа G верно неравенство

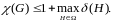
 Теорема очевидна для пустых графов. Пусть G — произвольный -хроматический граф,   2, а H – его минимальный порожденный подграф, удовлетворяющий условию (H) = . В этом случае (H – v)   – 1 для любой вершины v графа H.

Какова степень вершины v в H ? Предположим, что deg v <  – 1. Граф H – v правильно раскрасим  – 1 цветами. Окрасив затем вершину v в один из этих цветов, не использованный при окраске смежных с ней вершин, получим правильную ( – 1)-раскраску графа H. Из полученного противоречия следует deg v   – 1 и . 

Как и ранее, через  обозначим наибольшую из степеней вершин графа G.

Следствие 15.3. Для любого графа G верно неравенства (G)  1 + (G).

Некоторое улучшение последней оценки дает следующая

Теорема 15.4. (Брукс, 1941 г.) Если G — связный граф, не являющийся полным, и (G)  3 , то (G)  1 + (G).

Оценка, устанавливаемая теоремой Брукса, достижима (например, на графе, состоящем из цикла нечетной длины и единственной висячей вершины). Однако теорема может дать и завышенную оценку хроматического числа. Например, из этой теоремы следует, что (K_1,n)  n, в то время как (K_1,n) = 2.

2. Разбиение чисел на слагаемые. Диаграммы Ферре. Число всех отображений, число сюръективных отображений конечных множеств (элементы в и неразличимы).

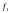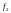Рассмотрим теперь отображения X* в Y*. Для того, чтобы отображения и различались, необходимо, чтобы различались наборы чисел { | f₁ ^–1( y₁ ) |, | f₁ ^–1( y₂ ) | , . . . , | f₁ ^–1( y_n ) | } и { | f₂ ^–1( y₁ )|,

| f₂ ^–1(y₂) |, . . . , | f₂ ^–1(y_n) | } (без учета порядка этих чисел). Таким образом, задача нахождения числа N(m, n) отображений X* в Y* эквивалентна нахождению числа разложений натурального числа m в сумму n неотрицательных целых слагаемых (порядок слагаемых не учитывается).

Обозначим через P(m, k) число разбиений m на k натуральных слагаемых. Понятно, что P(m, n) дает нам число сюръективных отображений из X* в Y*, а число произвольных отображений равно

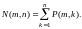
Изучать некоторые свойства P(m, k) помогают диаграммы Ферре (или Феррерса). Диаграмма Ферре для разложения m = a₁ + a₂ + … + a_k (для единообразия считаем, что a₁  a₂  …  a_k ) состоит из k строк, где строка i содержит a_i точек, расположенных в столбцах 1, 2,…, a_i . Ниже слева изображена диаграмма Ферре для разложения 16 = 6 + 5 + 2 + 2 + 1.

Утверждение 7.7 Число разложений числа m в сумму ровно k слагаемых равно числу представлений m в виде суммы натуральных слагаемых, наибольшее из которых равно k .

 Поставим в соответствие каждой диаграмме Ферре D разбиения m на k слагаемых сопряженную (или двойственную) ей диаграмму, полученную «транспонированием» D. Очевидно, «транспонированная» диаграмма отвечает некоторому разложению m = a₁ + a₂ + … + a_s с a₁ = k. Например, сопря

женная диаграмма, показанная выше справа, отвечает разложению 16 = 5 + 4 + 2 + 2 + 2 +1. Легко убедиться, что указанное соответствие взаимно однозначно отображает множество диаграмм с k строками на множество диаграмм с k столбцами. 

Если диаграмма совпадает со своей сопряженной диаграммой, то как такие диаграммы, так и соответствующие разложения числа называются самосопряженными.

Утверждение 7.8. Число самосопряженных разложений числа m равно числу таких представлений m, которые состоят из неравных нечетных слагаемых.

 Самосопряженность равносильна тому, что диаграмма Ферре симметрична относительно главной диагонали (см. пример ниже для разбиения 20 = 5 + 5 + 4 + 4 + 2). Поставим каждой такой диаграмме новое разбиение, пересчитав все точки диаграммы по-другому. Именно, разложим диаграмму на уголки (каждый уголок даст число нового разбиения), как показано на рисунке.

Осталось отметить два простых факта: число точек в уголке всегда нечетно (самосопряженность!) и каждый уголок имеет разное число точек. Приведенная диаграмма соответствует следующему разбиению числа 20 на неравные нечетные слагаемые: 20 = 9 + 7 +3 + 1. 

Без доказательства отметим еще одно свойство разбиений.

Утверждение 7.9. Число представлений числа m в виде суммы попарно различных натуральных слагаемых равно числу представлений m в виде суммы нечетных слагаемых.

БИЛЕТ 17