
Графи: представлення і обходи
1 Поняття графа
Графові моделі мають велике значення, оскільки використовуються у всіх задачах, де беруть участь кілька обє’єктів, з’єднаних між собою довільним чином (наприклад, комп'ютерні і транспортні мережі).
Отже, введемо основні визначення.
Графом G є пара (V,E) де
V є множиною вершин (vertices or nodes)
E є множиною ребер, які зв’язують вершини (set of edges)
Приклад:
V = {1,2,3,4,5}
E = {(1,2), (1,3), (1,4), (1,5), (2,3), (3,4), (4,5),(5,2)}

Рис.1 Граф
Оскільки ребра можуть іти від будь-якої вершини до будь-якої іншої, тому може бути важлива орієнтація ребер (див. Рис.2). Граф називається орієнтірованним (або орграфом), якщо для кожного ребра виділений напрямок.

Рис.2 Орієнтований граф
Приклад
V = { 1,2,3,4,5}
![]()
Повний граф
Повний граф – це граф у якого всі з’єднані всі пари вершин.

Рис. 3 Повний граф
Якщо в графі з будь-якої вершини можна дістатися до будь-якої іншої, переміщаючись від вершини до вершини по ребрах, такий граф називається зв'язаним.
Послідовність вершин, сполучених ребрами, називається шляхом.
Замкнутий шлях називається циклом.
Зважений граф
A weighted graph G = (V,E,W) is a graph where each edge e in E has a weight denoted by W(e)

Рис.4 Зважений граф
The weight of a Graph is the sum of the weights of the edges of the graph
2. Представлення графів

Рис. 5 Граф
Работая с графами в программе, необходимо выбрать способ хранения данных в памяти. Эти данные могут быть разного рода. Во-первых, необходимо хранить информацию о ребрах, то есть о том, какие вершины связаны между собой. Во-вторых, в каждой вершине может храниться какая-либо полезная информация (номер, название, цвет, служебные флаги для работы того или иного алгоритма и т.д.). Вообще говоря, на ребрах тоже может храниться такая информация.
Одно из возможных представлений графа подсказывает приведенное выше определение: можно хранить массив вершин и массив пар номеров вершин, представляющий ребра.
Так граф, приведенный на рис. будет храниться так
V = {1,2,3,4,5}
E = {(1,2), (1,3), (1,4), (1,5), (2,3), (3,4), (4,5),(5,2)}
Однако такое представление не очень эффективно для большинства задач: проверка смежности двух вершин занимает время, пропорциональное количеству ребер, а таких проверок может понадобится очень много, если мы, например, ищем путь.
Далее рассматриваются более эффективные представления графов.
Матриця суміжності
Вершины графа со всей информацией о них можно хранить в массиве – это обеспечивает быстрый доступ и не вносит дополнительных сложностей. Пусть вся информация представления в виде полей некоторого класса Vertex. Тогда для хранения V вершин нам понадобится массив.
Vertex[] v = new Vertex[V];
Операция проверки смежности двух вершины, то есть проверки существования ребра, выполняется очень часто, поэтому представление графа должно обеспечивать быстрое выполнение этой операции.
Для этого можно использовать так называемую матрицу смежности. Эта матрица представляет из себя квадратный массив VxV чисел, где N – число вершин в графе.
int[][] m = new int[V][V];
Информация о ребрах хранится так (будем считать граф ориентированным): в ячейке m[i, j] хранится количество ребер из вершины v[i] в вершину v[j]. То есть для ориентированного графа с рис. 1 матрица будет такой:
Для неорієнтованого графа

|
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
0 |
1 |
3 |
1 |
1 |
0 |
1 |
0 |
4 |
1 |
0 |
1 |
0 |
1 |
5 |
1 |
1 |
0 |
1 |
0 |
Для орієнтованого графа
|
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
Для зваженого графа

|
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
3 |
3 |
3 |
2 |
1 |
0 |
2 |
0 |
3 |
3 |
3 |
3 |
0 |
1 |
0 |
4 |
2 |
0 |
1 |
0 |
5 |
5 |
2 |
3 |
0 |
5 |
0 |
Зручно:
Добавляти і видаляти ребра
Перевіряти суміжність вершин
Незручно
Добавляти і видаляти вершини
Працювати з розрідженими графами
Если необходимо хранить дополнительную информацию о ребрах (например, «пропускную способность» или что-то еще), можно хранить матрицу из указателей на объекты, в которых хранится соответствующая информация. Нет объекта – нет ребра.
Матриця інцидентності

Для неорієнтованого графа

|
A |
B |
C |
D |
E |
F |
G |
H |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
3 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
5 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Для орієнтованого графа
Для зваженого графа
Зручно:
Міняти навантаження на ребра
Перевіряти інцидентність
Незручно
Добавляти і видаляти вершини
Працювати з розрідженими графами
Списки суміжності



Зручно:
Шукати вершини суміжні з даною
Добавляти ребра і вершини
Працювати із розрідженими графами
Незручно
Перевіряти присутність ребра
Видаляти ребра і вершини
Список ребер

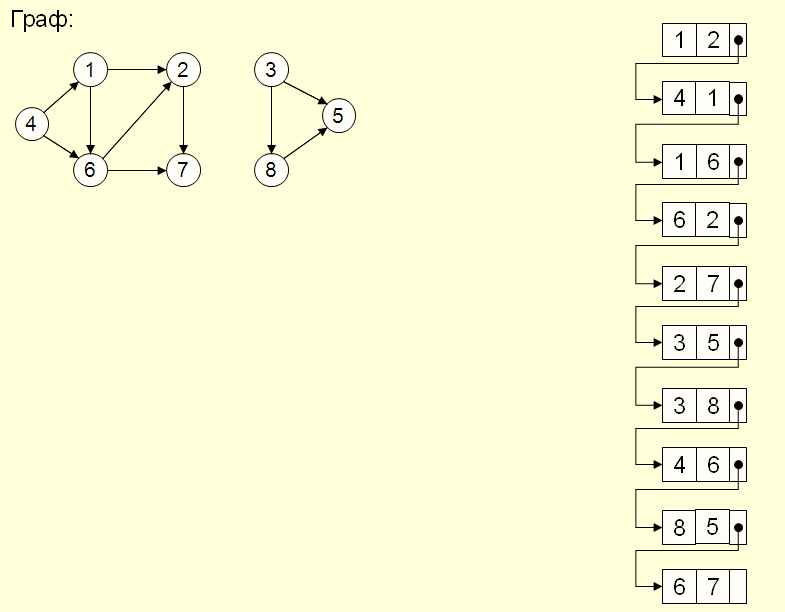

Зручно:
Видаляти і добавляти ребра і вершини
Впорядковувати ребра за зростанням навантаження
Працювати із розрідженими графами
Незручно
Визначати суміжність ребер і вершин
Осуществлять перебор инцидентных заданной вершине ребер
Обход графа в глубину
Несмотря на то, что перебрать все вершины графа (в отличие от вершин двоичного дерева) можно простым циклом for, поскольку они хранятся в массиве, часто возникает необходимость обойти граф, переходя от одной вершине к другой только в том случае, если они соединены ребром.
Например, это необходимо, чтобы узнать, до каких вершин можно добраться из данной.
На графах применяются те же алгоритмы обхода, что и на деревьях, то есть обходы в ширину и в глубину.
Рассмотрим обход в глубину. Этот алгоритм для графов, как и для деревьев, реализуется рекурсивно, однако есть одно важное отличие: в графе могут быть циклы. По такому циклу можно ходить бесконечно, поэтому необходимо как-то помечать вершины, в которых мы уже были, чтобы остановить рекурсию.
Хранить информацию о посещении вершины можно в специальном поле класса Vertex, а можно – в отдельном массиве флагов, где влаг с номером i говорит о том, была ли пройдена i-тая вершина.
Перед началом обхода необходимо записать установить все флаги посещения равными false.
Теперь – рекурсивная процедура обхода (от вершины i):
1. Если вершина i пройдена, выйти
2. Отметить вершину i как пройденную
3. Вызвать процедуру обхода от всех вершин, смежных с i
То есть пройти по i-той строке матрицы и вызвать себя от тех j, для которых m[i, j] <> 0.
Ясно, что, если граф не связный, вызов этой процедуры от первой вершины не даст обхода всего графа – будут пройдены только вершины, достижимые из начальной. Чтобы обойти весь граф, нужно вызвать процедуру обхода от всех вершин по очереди: если какая-то из них окажется пройденной ранее, она будет уже отмечена как пройденная, и процедура просто закончится на первой же строке.
Топологическая сортировка
Интересным приложением поиска в глубину является задача о топологической сортировке ориентированного графа.
Пусть есть набор действий {A, B, C, D, E, F}, которые нужно выполнить. Причем A можно выполнить только после F, B – после С и A, С – после E, а D – после B.
В каком порядке нужно выполнять действия?
Нарисуем граф из действий: ребро идет из A в B, если B нужно делать после A.

Задача нахождения последовательности действий эквивалентна задаче о расстановке вершин в таком порядке, чтобы все ребра показывали слева направо (это и называется топологической сортировкой графа). Если в графе есть циклы, то это невозможно, поэтому топологическая сортировка работает только для ациклических графов.
Итак, результат сортировки приведенного графа таков:

Это не единственная возможная сортировка: например, вершину E можно перенести прямо перед C и т.д.
Как получить решение в общем случае?
Возьмем произвольную вершину, например, C. Обойдем в глубину все вершины, достижимые из нее: получим следующий результат: С встретилась первой, B – второй, D – третьей. Пройден еще не весь граф. Возьмем еще одну вершину (из не пройденных). Эта вершина недостижима из C – иначе она была бы пройдена – значит, ее (и все вершины, достижимые из нее) можно поставить раньше, чем C – нет необходимости ставить позже.
Пусть мы взяли вершину F: вершины F и A встанут перед C именно в названном порядке, потому что A встретилась позже, чем F.
Снова возьмем произвольную не пройденную вершину: осталась только E. Ее можно поставить перед F и перед C, то есть на первое место.
Общая логика рассуждений такова: обход в глубину выдает все вершины, стоящие после данной в нужном порядке. Остальные вершины нужно ставить раньше, потому что они точно не позже.
Заметим, что при рекурсивном обходе графа, процедура обхода вызывает сама себя от вершин смежных с данной (назовем ее X) – эти вызовы обходит все вершины стоящие после X, саму вершину X нужно поставить раньше всех достижимых из нее.
Заведем список, в который будем добавлять вершины. Мы каждый раз ставим вершину раньше всех пройденных, поэтому будем добавлять в начало списка: прошли все вершины, стоящие после данной – теперь можно добавить ее.
Итак, имея рекурсивную реализацию обхода в глубину, мы можем построить топологическую сортировку графа следующим образом:
1. Если вершина i пройдена, выйти
2. Отметить вершину i как пройденную
3. Вызвать процедуру обхода от всех вершин, смежных с i
Этот вызов добавит в список все вершины, стоящие после текущей.
4. Добавить текущую вершину в начало списка.
Приведенная процедура добавляет вершину, когда все достижимые из нее уже пройдены рекурсивными вызовами и добавлены, поэтому сама эта вершины будет стоять раньше достижимых из нее.
«Наивный» алгоритм нумерации вершин:
Находим какую-либо вершину, в которую не входят дуги, нумеруем ее.
Помечаем дуги, выходящие из помеченной вершины, как «не существующие».
Повторяем шаги (1) и (2), пока не будут занумерованы все вершины.

«Эффективный» алгоритм нумерации вершин:
Производим обход графа с помощью рекурсивной процедуры обхода, начиная с произвольной вершины.
Нумеруем каждую вершину при «прохождении ее назад» максимальным из номеров (то есть нумерация происходит в порядке убывания номеров).
Повторяем шаги (1) и (2), пока не останется непройденных вершин.

+індивідуалка № варіанту то є № області в Україні
[21:39:18] Pavlo Denysyuk: з обл.центру прокладайте дорогу
[21:39:51] Pavlo Denysyuk: вершини гарафа обл.центр та районний центр
[21:40:03] Pavlo Denysyuk: вага ребра, відстань в км
