МІНІСТЕРСТВО ОСВІТИ І НАУКИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ „ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Вступ до теорії графів методичні вказівки

до виконання практичних робіт

з дисципліни „Комп’ютерна дискретна математика”

для студентів спеціальності

6. 050103 „Програмна інженерія”

Затверджено на засіданні кафедри програмного забезпечення Протокол № __ від _______ р.

Львів – 2015

Теорія графів. :Методичні вказівки до виконання практичних робіт із дисципліни „Комп’ютерна дискретна математика” для студентів спеціальності „Програмна інженерія” / Укл.: П.В. Сердюк, О.О. Нитребич, Н.А. Крупко – Львів: Видавництво Національного університету „Львівська політехніка”, 2015. –??с.

УкладачіП.В. Сердюк, кандидат техн. наук, доц. О.О. Нитребич, асист. кафедри ПЗ

Н.А. Крупко, асист. кафедри ПЗ

Відповідальний за випуск Федасюк Д.В., д-р тех. наук, проф.

Рецензенти, канд. тех. наук, доц.

, канд. фіз.-мат. наук, доц.

Мета роботи:Ознайомитись на практиці із основними поняттями теорії графів.

Теоретичні відомості Вступ

Теорія графів має широке застосування в моделюванні інформаційних процесів, у програмуванні й у вирішенні економічних завдань.

Перша згадка про неї зустрічається в роботах Ейлера, який у1736 році розв’язав задачу про кенігсберзькі мости.

У Кенігсберзі було два острови, з’єднаних сімома мостами з берегами річки Прегель та один із одним (рис. 1). Суть задачі полягала в пошуку маршруту проходження всіх чотирьох частин суші, який мав починатися на будь-якій частині суші та закінчуватися на ній же за умови проходження кожного моста по одному разу. Проте всі спроби знайти маршрут були невдалими.

Щоб довести не існування такого маршруту, Ейлер позначив кожну частину суші точкою (вершиною або вузлом), а кожен міст – лінією (ребром), що з’єднує відповідні точки, і отримав “граф” (рис. 1). Твердження про не існування маршруту тотожна неможливості деяким чином обійти граф. Виходячи з цього конкретного випадку, Ейлер узагальнив постановку задачі та знайшов критерій існування обходу.

Пізніше елементи теорії графів з’явилися в таких природничих науках, як географія, фізика, хімія, електротехніка. У загальному, графи використовуються в усіх галузях, де є елементи та зв’язки між ними, тому теорія графів є актуальним прикладним розділом математики.

Рис. 1 Кенігсберзькі мости та граф

1. Основні означення теорії графів

У загальному випадку граф – це множина Vточок, певним чином з'єднаних між собою лініями, необов'язково прямими. Точки множиниVназиваютьсявершинамиграфа, а лінії, які їх з’єднують –ребрами.

Вершини графа зазвичай нумерують десятковими числами, але можна використовувати і будь-які інші знаки. Якщо вершини пронумеровані, то ребра означають неупорядковані пари номерів вершин. Кожну пару утворюють номери тих вершин, які з'єднані ребром.

Означення 1.1.Простий граф – це параG=(V,E), деV – непорожня скінченна множина вершин,Е – множина невпорядкованих пар різних елементів ізV (множина ребер).

Приклад 1.1. Розглянемо простий граф, наведений на рис. 1.1. Такий граф складається з множини вершинV={1,2,3,4,5,6,7} та множини реберЕ = {{1,2}, {1,3}, {1,4}, {1,7}, {2,5}, {2,6}, {2,7}, {3,4}, {3,6}, {4,5}, {4,6}, {5,7}}

Рис.1.1 Простий граф

Класифікація графів.

Усі графи в загальному поділяються на неорієнтовані та орієнтовані.

Означення 1.2.Орієнтований граф (або орграф) – це параG=(V,E), деV – непорожня скінченна множина вершин,Е – множина впорядкованих пар елементів ізV. Орієнтовані ребра називаютьдугамиПриклад орграфу наведений на рис. 1.2, б.

Означення 1.3. Граф, що має орієнтовані та неорієнтовані ребра одночасно, називається змішаним (рис. 1.3, в).

а)	б)	в)
Рис.1.2 Приклади графів а) неорієнтований граф; б) орієнтований граф; в) змішаний граф

Існують графи, у яких деякі вершини можуть бути з’єднані не одним ребром (дугою), а декількома. Такі ребра (дуги) називаються кратними. Крім цього графи можуть містити ребра, які з’єднують вершину саму з собою, та називаютьсяпетлями.

Означення 1.4. Неорієнтований мультиграф – це параG=(V,E), деV – непорожня скінченна множина вершин,Е – сім’я невпорядкованих пар різних елементів ізV. Тобто це граф, що містить кратні ребра (рис. 1.3,а).

Означення 1.5. Неорієнтований псевдограф – це параG=(V,E), деV – непорожня скінченна множина вершин,Е – множина впорядкованих пар не обов’язково різних елементів ізV. Тобто це граф, що містить петлі (рис. 1.3,б).

Означення 1.6. Орієнтований мультиграф – це параG=(V,E), деV – непорожня скінченна множина вершин,Е – сім’я впорядкованих пар елементів ізV. Тобто це граф, що містить кратні дуги (рис. 1.3,в).

а)	б)	в)
Рис.1.3. Приклади графів а) неорієнтований мультиграф; б) неорієнтований псевдограф; в) орієнтований мультиграф

Отже, усі типу графів можна представити у вигляді діаграми (рис.1.4):

Рис. 1.4 Класифікація графів

За допомогою графів зображуються структурні залежності між елементами. Наприклад, у електричній схемі, в молекулі, яка складається з атомів, або у схемі міського транспорту. Для побудови графа, що відповідає транспортній схемі, вершинами можна подати зупинки, а ребрами – ділянки маршрутів між ними. Схему доріг міста можна представити у вигляді мультиграфа, вершини якого відповідають перехрестям, а ребра – вулицям. Існують вулиці з одностороннім рухом, тому задається напрям руху по них (приклад орграфу).

Об’єднання, перетин, доповнення графів.

Означення 1.7. Об’єднанням графівG₁={V₁,Е₁} таG₂={V₂,Е₂} називають графG=G₁G₂ = {V, Е}, деV =V₁V₂;Е =Е₁Е₂.

Приклад 1.2. Розглянемо об’єднання графів, зображених на рисунку 1.5.

Рис. 1.5 Приклад об’єднання графів

Приклад 1.3.Очевидно, що якщо V₁ = V₂таЕ₁⊂Е₂, тодіG=G₁G₂ =G₂ (рис. 1.6).

Рис. 1.6 Приклад об’єднання графів

Означення 1.8. Перетином двох графівG₁таG₂називається графG=G₁G₂ ={V,Е}, деV=V₁V₂;Е=Е₁Е₂.

Приклад 1.4.Розглянемо перетин графів, зображених на рисунку 1.7.

Рис. 1.7 Приклад перетину графів

Із означення випливає, що G =G₁G₂ =, якщоV₁V₂ =, тобто якщо існує два графи, які не мають однаково позначених вершин, то їх перетином буде пустий граф (рис.1.8).

Рис. 1.8 Приклад перетину графів

Приклад 1.5.ЯкщоV₁V₂ , аЕ₁Е₂ =, тоG =G₁G₂ буде нуль-графом, множина вершин якого дорівнюєV₁V₂ (рис. 1.9)

Рис. 1.9 Приклад перетину графів

Означення 1.9. Доповненням до графуG називається граф, який містить ту ж саму кількість вершин, які з’єднані ребрами лише тоді в графі, коли вони не з’єднані в графіG.

Рис. 1.10 Приклад доповнення графу

Суміжність вершин, інцидентність вершин та ребер, степінь вершин.

Означення 1.9. Дві вершини називаються суміжними у неорієнтованому графі, якщо вони з’єднані ребром.

Приклад 1.5.На рис. 1.11 суміжними є вершини 1 і 2, 1 і 3, 2 і 5, 2 і 6, 3 і 6.

Означення 1.10. Два ребра називаються суміжними, якщо вони мають спільний кінець.

Приклад 1.6.На рис. 1.11 суміжними ребрами є {1,2} і {2,5}, {1,2} і {1,3}, {3,6} і {6,2}, {2,5} і {2,6}.

Означення 1.10. Вершина і ребро є інцидентними, якщо вершина є кінцем даного ребра.

Приклад 1.7.На рис. 1.11 вершина 1 інцидентна ребрам {1,2} та {1,3}.

Рис. 1.11 Приклад неорієнтованого графу

Означення 1.11. В орієнтованому графі початковою (ініціальною) вершиною називається та, з якої дуга виходить, а кінцевою (термінальною) – в яку дуга входить.

Приклад 1.8.На рис. 1.12 вершина 2 є кінцем дуг (1,2), (4,2) та початком дуг (2,3), (2,4). Зауважимо, що вершина 4 є одночасно початком та кінцем для петлі (4,4).

Рис. 1.12 Приклад орієнтованого графу

Означення 1.12.Степенем вершини у неорієнтованому графі – це кількість інцидент них ребер цій вершині.

Зауважимо, що петля враховується двічі. Позначається степінь вершини як deg(v).

Означення 1.13.Якщо степінь вершини дорівнює нулю (deg(v)=0), то така вершина називається ізольованою.

Означення 1.14.Якщо степінь вершини дорівнює одиниці (deg(v)=1), то така вершина називається висячою.

Приклад 1.8.На рис. 1.13 вершина 1 є висячою deg(1)=1,вершина 7 є ізольованою deg(7)=0, степінь вершини 3 дорівнює двом, бо ця вершина інцидентна ребрам {3,4} та {3,6} (deg(3)=2).

Рис. 1.13 Приклад неорієнтованого графу

ТЕОРЕМА 1.Якщо графG=(V,E) – неорієнтований граф ізmребрами, то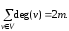

Це твердження стосується як і простого, так і мульти- та псевдографа.

ТЕОРЕМА 2.Неорієнтований граф має парну кількість вершин непарного степеня.

Приклад 1.9.Чи існує простий граф зі степенями вершин 2,2,3,3,3,3?

Відповідь:Так, адже даний граф має парну кількість вершин непарного степеня. Окрім того його можна побудувати (рис.1.14).

Рис.1.14 Граф зі степенями вершин 2,2,3,3,3,3

Приклад 1.10.Чи існує простий граф зі степенями вершин 1,2,3,4,5,6,7?

Відповідь:Ні, хоча даний граф має парну кількість вершин непарного степеня, але наявність вершини зі степенем 7 означає, що вона суміжна зі сімома вершинами графу. Так як вершин є 7, то виходить, що існує як мінімум одне кратне ребро. Тобто граф не є простим.

У орієнтованому графі існують поняття півстепеня входу та виходу.

Означення 1.15. Півстепенем входу вершиниvорієнтованого графу – це кількість дуг, для яких вершинаvє кінцевою.

Півстепінь входу позначається deg^-(v).

Означення 1.16. Півстепенем виходу вершиниvорієнтованого графу – це кількість дуг, для яких вершинаvє початковою.

Півстепінь виходу позначається deg⁺(v).

Приклад 1.11.У графі, зображеному на рис.1.15, deg^-(1)=2, deg⁺(1)=0, deg^-(2)=2, deg⁺(2)=0, deg^-(3)=1, deg⁺(3)=3, deg^-(4)=1, deg⁺(4)=3.

Рис.1.15 Орієнтований граф

ТЕОРЕМА 3.Якщо графG=(V,E) – орієнтований мультиграф ізmдугами, то

Приклад 1.12.У графі, зображеному на рис.1.15, deg^-(1)=2, deg⁺(1)=0, deg^-(2)=2, deg⁺(2)=0, deg^-(3)=1, deg⁺(3)=3, deg^-(4)=1, deg⁺(4)=3.