§ 7. Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0 < р < 1) и, следовательно, вероятность его непоявления q=1—р. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в k-м испытании, то в предшествующих k—1 испытаниях оно не появлялось.

Обозначим через X дискретную случайную величину — число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями X являются натуральные числа: x₁=1, х₂=2, ...

Пусть в первых k—1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

P(X=k)=q^k-1p. (*)

Полагая k=1,2, ... в формуле (*), получим геометрическую прогрессию с первым членом р и знаменателем q (0< q<1):

p,qp,q²p, … ,q^k-1p,… (**)

По этой причине распределение (*) называют геометрическим.

Легко убедиться, что ряд (**) сходится и сумма его равна единице. Действительно, сумма ряда (**)

p/(1-q)=p/p=1.

Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. По условию, р=0,6, q = 0,4, k=3. Искомая вероятность по формуле (*)

P= q^k-1p =04²* 0,6 = 0,096.

§ 8. Гипергеометрическое распределение

Прежде чем дать определение гипергеометрического распределения, рассмотрим задачу. Пусть в партии из N изделий имеется М стандартных (М < N). Из партии случайно отбирают п изделий (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима). Обозначим через X случайную величину—число т стандартных изделий среди п отобранных. Очевидно, возможные значения X таковы: 0, 1, 2, ..., min (M, п).

Найдем вероятность того, что Х = т, т. е. что среди п отобранных изделий ровно т стандартных. Используем для этого классическое определение вероятности.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь п изделий из N изделий, т. е. числу сочетаний .

Найдем число исходов, благоприятствующих событию Х = m (среди взятых п изделий ровно m стандартных); т стандартных изделий можно извлечь из М стандартных изделий способами; при этом остальные п — т изделий должны быть нестандартными; взять же п—т нестандартных изделий из N — т нестандартных изделий можно способами. Следовательно, число благоприятствующих исходов равно (см. гл. I, § 4, правило умножения).

Искомая вероятность равна отношению числа исходов, благоприятствующих событию Х = т, к числу всех элементарных исходов

P(X=m)= . (*)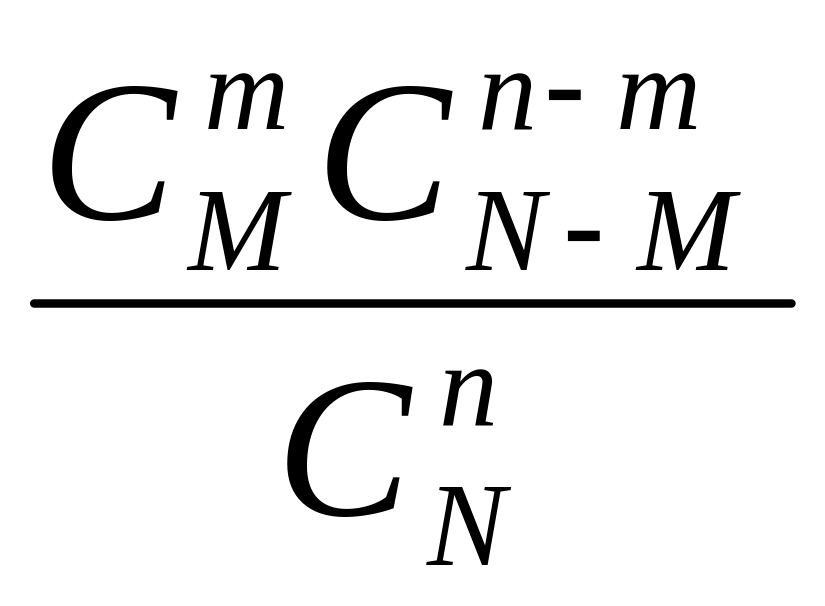

Формула (*) определяет распределение вероятностей, которое называют гипергеометрическим.

Учитывая, что т—случайная величина, заключаем, что гипергеометрическое распределение определяется тремя параметрами: N, М, п. Иногда в качестве параметров этого распределения рассматривают N, п и p = M/N, где р — вероятность того, что первое извлеченное изделие стандартное.

Заметим, что если п значительно меньше N (практически если n<0,1N), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.

Пример. Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.

Решение. По условию, N=50, M= 0, n = 5,m = 3. Искомая вероятность

P(X = 3) = = 0,234.

Задачи

1. Возможные значения случайной величины таковы: x₁ = 2, x₂ = 5, x₃ = 8. Известны вероятности первых двух возможных значений: р₁=0,4, р₂ = 0,15. Найти вероятность х₃.

Отв. p₃= 0,45.

2.Игральная кость брошена 3 раза. Написать закон распределения числа появлений шестерки.

Отв.

X	3	2	1	0
P	1/216	15/216	75/216	125/216

3.Составить закон распределения вероятностей числа появлений события А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0,6.

Отв.

K	0	1	2	3
P	0,064	0,288	0,432	0,216

4.Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,004. Найти вероятность того, что в течение 1 мин обрыв произойдет на пяти веретенах.

Отв. Р₁₀₀₀ (5) = 0,1562.

5. Найти среднее число опечаток на странице рукописи, если вероятность того, что страница рукописи содержит хотя бы одну опечатку, равна 0,95. Предполагается, что число опечаток распределено по закону Пуассона.

Указание. Задача сводится к отысканию параметра X из уравнения =0,05.

Отв. 3.

6. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение 1 мин абонент позвонит на коммутатор, равна 0,02. Какое из двух событий вероятнее: в течение 1 мин позвонят 3 абонента; позвонят 4 абонента?

Отв. P₁₀₀(3) = О,18; Р₁₀₀ (4) =0,09.

7.Рукопись объемом в 1000 страниц машинописного текста содержит 1000 опечаток. Найти вероятность того, что наудачу взятая страница содержит: а) хотя бы одну опечатку; б) ровно 2 опечатки; и) не менее двух опечаток. Предполагается, что число опечаток распределено по закону Пуассона.

Отв. а) Р=1—е^-1 = 0,6321; б) Р₁₀₀₀ (2) = 0,18395; в) Р = 0,2642.

8. Среднее число вызовов, поступающих на АТС в 1 мин, равно 5. Найти вероятность того, что за 2 мин поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов.

Указание, е^-10 = 0,000045.

Отв. а) 0,00225; б) 0,000495; в) 0,999505.

9.Производится бросание игральной кости до первого выпадения шести очков. Найти вероятность того, что первое выпадение «шестерки» произойдет при втором бросании игральной кости.

Отв. Р(Х = 2) = 5/36.

10.В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 5 взятых наудачу деталей окажется 3 стандартных.

Отв. Р(Х=3) = 14/33.