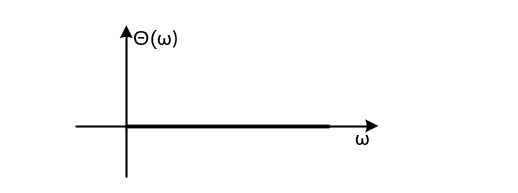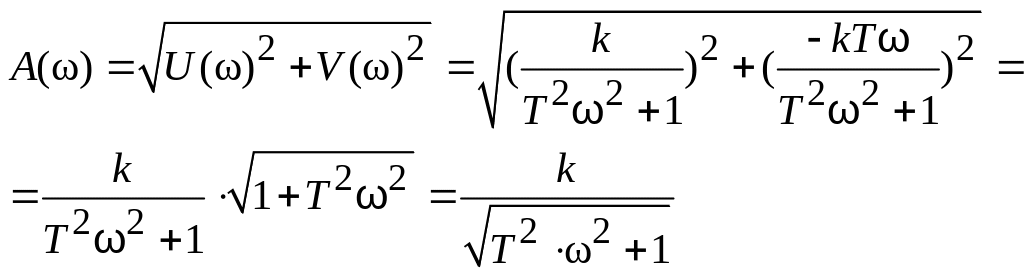- •Глава 2. Характеристики и свойства типовых линейных звеньев
- •2.1. Типовые линейные звенья
- •Глава 3. Эквивалентные преобразования структурных схем, их математическое описание
- •3.1.1. Общие замечания
- •3.1.2. Последовательное соединение звеньев
- •3.1.3. Согласно-параллельное соединение звеньев
- •3.1.4. Встречно-параллельное соединение звеньев
Глава 2. Характеристики и свойства типовых линейных звеньев
2.1. Типовые линейные звенья
Для исследования поведения САУ в переходных режимах целесообразно рассматривать отдельные элементы ее только с точки зрения динамических свойств независимо от их конкретного исполнения и физической природы происходящих в них явлений. При представлении САУ в виде структурных схем такие элементы называют звеньями. Среди звеньев линейных систем можно выделить простейшие типовые, для которых характерно следующее:
наличие одного воздействия на входе и одной величины на выходе;
односторонняя передача воздействия с входа на выход;
переходный процесс описывается линейным дифференциальным (в частном случае алгебраическим) уравнением не выше второго порядка с постоянными коэффициентами.
По виду дифференциального уравнения различают следующие типы звеньев:
безынерционное (усилительное);
инерционное первого порядка (апериодическое);
колебательное и инерционное второго порядка;
дифференцирующее;
интегрирующее (астатическое);
интегродифференцирующее;
запаздывающее.
В литературе встречаются и несколько отличные от указанных типы и названия звеньев. Для типовых звеньев применимы рассмотренные в 1.7 понятия характеристик САУ.
2.2. Уравнения, передаточные функции и примеры реализации типовых звеньев
а) Безинерционные:
Звено принято называть безинерционным, если связь между входом и выходом звена определяется алгебраическим уравнением вида
хвых(t) = k∙хвх(t) |
(2.1) |
где k – коэффициент передачи или усиления.
Уравнение в операторной форме:
хвых(р) = k∙хвх(р) |
(2.2) |
Передаточная функция:
W(p) = k = хвых(р)/ хвх(р) |
(2.3) |
Согласно
формуле (1.10)
![]() ,т.е.
степени характеристического полинома
D(p)
и комплексного коэффициента передачи
K(p)
равны 0 (n=0
и m=0).
Так как условие n≥m
выполняется, то система технически
реализуема.
,т.е.
степени характеристического полинома
D(p)
и комплексного коэффициента передачи
K(p)
равны 0 (n=0
и m=0).
Так как условие n≥m
выполняется, то система технически
реализуема.
Переходная характеристика.
Она определяется по формуле 1.15
![]() .
.
Так как характеристическое уравнение (D(p)=1)=0 корней pk не имеет, то необходимо найти только значения комплексного коэффициента передачи при 0 (K(0)) и характеристического полинома при 0 (D(0)).
![]() ;
;
![]() .
.
Тогда
|
(2.4) |
Графики единичной функции и переходной характеристики представлены на рис. 2.1.
|
|
а) |
б) |
Рис 2.1. Графики единичной функции и переходной характеристики безинерционного звена |
|
Частотные характеристики:
- комплексная частотная функция:
W(jω) = k |
(2.5) |
- амплитудночастотная характеристика:
|
(2.6) |
- фазочастотная характеристика:
|
(2.7) |
Графические представления частотных характеристик безинерционного звена приведены на рис. 2.2.
|
а) |
|
б) |
|
в) |
Рис. 2.2. Графические представления частотных характеристик безинерционного звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Пример безинерционного звена представлен на рис. 2.3.
|
Рис 2.3. Пример реализации безинерционного звена |
Вывод уравнения динамики:
I(t)∙R1
+ U2(t)
= U1(t).
Учитывая,
что
![]() :
:
![]()
![]() – уравнение
динамики в алгебраическом виде;
– уравнение
динамики в алгебраическом виде;
![]() – уравнение
динамики в операторном виде, где
коэффициент усиления
– уравнение
динамики в операторном виде, где
коэффициент усиления
![]() .
.
б) Инерционное звено первого порядка.
Звено принято называть инерционным первого порядка, если связь между входом и выходом звена определяется дифференциальным уравнением вида
|
(2.8) |
где Т – постоянная времени, k – коэффициент передачи
Уравнение в операторной форме:
|
(2.9) |
Передаточная функция:
|
(2.10) |
Так как D(p)=T∙p+1 и K(p)=k, то условие (n=1) ≥ (m=0) выполняется и система технически реализуема.
Переходная характеристика.
Она определяется по формуле 1.15
.
D(p)=T∙p+1; K(p)=k.
K(0)=k; D(0)=1.
Характеристическое
уравнение (T∙p+1)=0
имеет корень
![]() .
Тогда
.
Тогда
![]() .
.
Первая
производная характеристического
полинома равна
![]() .
При p=p1
.
При p=p1
![]() .
.
Тогда
|
(2.11) |
График переходной характеристики представлен на рис. 2.4.
|
Рис 2.4. График переходной характеристики инерционного звена первого порядка |
Частотные характеристики:
- комплексная частотная функция:
|
(2.12) |
- амплитудно-частотная характеристика:
|
(2.13) |
- фазочастотная характеристика:
|
(2.14) |
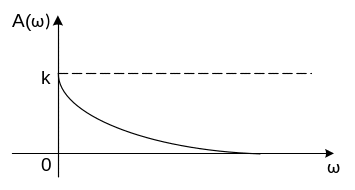
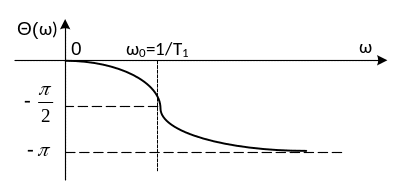
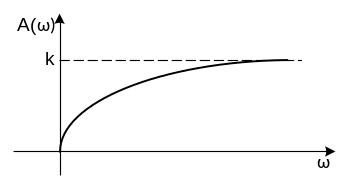
Графические представления частотных характеристик инерционного звена первого порядка приведены на рис. 2.5.
|
а) |
|
б) |
|
в) |
Рис. 2.5. Графические представления частотных характеристик безинерционного звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Пример инерционного звена первого порядка представлен на рис. 2.6.
|
|
а) |
б) |
Рис. 2.6. Примеры реализации инерционного звена первого порядка |
|
Вывод уравнения динамики для примера, представленном на рис. 2.6, а):
I(t)∙R
+ U2(t)
= U1(t).
Учитывая, что
![]() :
:
![]() – уравнение
динамики.
– уравнение
динамики.
![]() – уравнение
динамики в операторной форме. При этом
– уравнение
динамики в операторной форме. При этом
![]() и
и
![]() .
.
Вывод уравнения динамики для примера, представленном на рис. 2.6, б), сделать самостоятельно.
в) Колебательное звено.
Звено принято называть колебательным, если связь между входом и выходом звена определяется дифференциальным уравнением вида
|
(2.15) |
где
Т1
и T2
– постоянная
времени, k
– коэффициент передачи, при чем Т1>0,
Т2≥0
и
![]() .
.
Уравнение в операторной форме:
|
(2.16) |
Передаточная функция:
|
(2.17) |
Так
как
![]() и K(p)=k,
то условие
(n=2)
≥ (m=0)
выполняется
и система
технически реализуема.
и K(p)=k,
то условие
(n=2)
≥ (m=0)
выполняется
и система
технически реализуема.
Переходная характеристика.
Для ее определения необходимо найти корни характеристического уравнения
|
(2.18) |
Отсюда:
|
(2.19) |
Если
![]() то корни p1,2
- вещественные, а звено называется
инерционным
второго порядка.
Оно не относится к простейшим типовым
звеньям, так как может быть представлено
двумя последовательно включенными
инерционными звеньями первого порядка
(рис. 2.7).
то корни p1,2
- вещественные, а звено называется
инерционным
второго порядка.
Оно не относится к простейшим типовым
звеньям, так как может быть представлено
двумя последовательно включенными
инерционными звеньями первого порядка
(рис. 2.7).
|
|
а) |
б) |
Рис. 2.7. Представление инерционного звена второго порядка двумя звеньями первого порядка: а) звено первого порядка состоит из двух индуктивностей и двух активных сопротивлений; б) звено первого порядка состоит из двух емкостей и двух активных сопротивлений |
|
Если передаточная функция одного инерционного звена первого порядка, представленного на рис. 2.7 равна
 ,
,
а второго
![]() ,
,
то передаточная функция последовательно соединенных звеньев первого порядка равна
![]()
Так
как условие
![]() выполняется всегда, то мы имеем
передаточную функцию инерционного
звена второго порядка.
выполняется всегда, то мы имеем
передаточную функцию инерционного
звена второго порядка.
Если
![]() ,
то корни
,
то корни
![]() - комплексные, а звено называется
колебательным и является простейшим.
Здесь α – декремент затухания, ω
- частота колебаний. T2
определяет наличие или отсутствие
затухания колебания. При T2=0
колебания будут незатухающими с частотой
- комплексные, а звено называется
колебательным и является простейшим.
Здесь α – декремент затухания, ω
- частота колебаний. T2
определяет наличие или отсутствие
затухания колебания. При T2=0
колебания будут незатухающими с частотой
![]() ,
которая называется собственной. Пример
колебательного звена с затухающими
колебаниями представлен на рис. 2.8. Здесь
,
которая называется собственной. Пример
колебательного звена с затухающими
колебаниями представлен на рис. 2.8. Здесь
![]() ,
,
![]() .
При этом декремент затухания
.
При этом декремент затухания
 .
.
|
Рис. 2.8. Пример колебательного звена с затухающими колебаниями |
Пример
колебательного звена с незатухающими
колебаниями представлен на рис. 2.9. Здесь
,
![]() .
При этом декремент затухания
.
При этом декремент затухания
![]() .
.
|
Рис. 2.9. Пример колебательного звена с незатухающими колебаниями |
Переходная характеристика колебательного звена описывается формулой
|
(2.20) |
График переходной характеристики представлен на рис. 2.10.
|
Рис 2.10. График переходной характеристики колебательного звена |
Частотные характеристики:
- комплексная частотная характеристика:
|
(2.21) |
При
этом
![]() и
и
![]()
- амплитудно-частотная характеристика:
|
(2.22) |
- фазочастотная характеристика:
|
(2.23) |
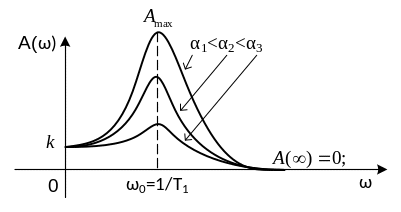
Графические представления частотных характеристик колебательного звена приведены на рис. 2.11.
|
а) |
|
б) |
|
в) |
Рис. 2.11. Графические представления частотных характеристик колебательного звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
г) Дифференцирующее звено.
Различают «идеальное» и реальное дифференцирующие звенья.
1. Идеальное дифференцирующее звено
Звено принято называть идеальным дифференцирующим, если связь между входом и выходом звена определяется уравнением вида
|
(2.24) |
где k – постоянный коэффициент, имеющий размерность времени.
Уравнение в операторной форме:
|
(2.25) |
Передаточная функция:
|
(2.26) |
Так
как
![]() и
и
![]() ,
то условие
(n=0)
≥ (m=1)
не выполняется
и такое звено
технически нереализуемо.
,
то условие
(n=0)
≥ (m=1)
не выполняется
и такое звено
технически нереализуемо.
Переходная характеристика:
|
(2.27) |
График переходной характеристики «идеального» дифференцирующего звена представлен на рис. 2.12.
|
Рис 2.12. График переходной характеристики «идеального» дифференцирующего звена |
Частотные характеристики:
- комплексная частотная функция:
|
(2.28) |
- амплитудно-частотная характеристика:
|
(2.29) |
- фазочастотная характеристика:
|
(2.30) |
Графические представления частотных характеристик «идеального» дифференцирующего звена приведены на рис. 2.13.
|
а) |
|
б) |
|
в) |
Рис. 2.13. Графические представления частотных характеристик «идеального» дифференцирующего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Пример «идеального» дифференцирующего звена представлен на рис. 2.14.
|
Рис. 2.14. Пример реализации «идеального» дифференцирующего звена |
2. Реальное дифференцирующее звено
Звено принято называть реальным дифференцирующим, если связь между входом и выходом звена определяется дифференцирующим уравнением вида
|
(2.31) |
где k – постоянный коэффициент, T – постоянная времени звена.
При
![]() ,
но при конечном
,
но при конечном
![]() уравнение
переходит в уравнение «идеального»
дифференцирующего звена.
уравнение
переходит в уравнение «идеального»
дифференцирующего звена.
Уравнение в операторной форме:
|
(2.32) |
Передаточная функция.
|
(2.33) |
Переходная характеристика:
Она определяется по формуле 1.15
.
D(p)=T∙p+1;
![]() .
.
K(0)=0; D(0)=1.
Характеристическое
уравнение (T∙p+1)=0
имеет корень
.
Тогда
![]() .
.
Первая производная характеристического полинома равна . При p=p1 .
Тогда

или окончательно
|
(2.34) |
График переходной характеристики реального дифференцирующего звена представлен на рис. 2.15.
|
Рис 2.15. График переходной характеристики реального дифференцирующего звена |
Частотные характеристики:
- комплексная частотная функция:
|
(2.35) |
- амплитудно-частотная характеристика:
|
(2.36) |
- фазочастотная характеристика:
|
(2.37) |
Графические представления частотных характеристик «идеального» дифференцирующего звена приведены на рис. 2.16.
|
а) |
|
б) |
|
в) |
Рис. 2.16. Графические представления частотных характеристик реального дифференцирующего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Примеры реального дифференцирующего звена представлены на рис. 2.17.
|
|
а) |
б) |
Рис. 2.17. Примеры реализации реального дифференцирующего звена |
|
Вывод уравнения динамики для примера, представленного на рис. 2.17, а):
Uc(t)+
U2(t)
= U1(t).
Учитывая, что
![]() :
:
![]() или,
учитывая, что
или,
учитывая, что
![]() :
:
![]() (*).
(*).
Продифференцируем обе части уравнения (*)
![]() – уравнение
динамики.
– уравнение
динамики.
![]() – уравнение
динамики в операторной форме. При этом
и
– уравнение
динамики в операторной форме. При этом
и
![]() .
.
Вывод уравнения динамики для примера, представленном на рис. 2.17, б), сделать самостоятельно.
Дифференцирующее звено широко используется для осуществления так называемой гибкой обратной связи, а также для создания воздействий по производным.
д) Интегрирующее звено.
Звено принято называть интегрирующим, если связь между входом и выходом звена определяется дифференциальным уравнением вида
|
(2.38) |
где k – постоянный коэффициент.
Уравнение в операторной форме:
|
(2.39) |
Передаточная функция:
|
(2.40) |
Переходная характеристика:
|
(2.41) |
График переходной характеристики интегрирующего звена представлен на рис. 2.18.
|
Рис 2.18. График переходной характеристики интегрирующего звена |
Частотные характеристики:
- комплексная частотная характеристика:
|
(2.42) |
- амплитудно-частотная характеристика:
|
(2.43) |
- фазочастотная характеристика:
|
(2.44) |
Графические представления частотных характеристик интегрирующего звена приведены на рис. 2.19.
|
а) |
|
б) |
|
в) |
Рис. 2.19. Графические представления частотных характеристик интегрирующего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Пример интегрирующего звена представлен на рис. 2.20.
|
Рис. 2.20. Пример реализации интегрирующего звена (входная величина – ток I(t), выходная – напряжения U2(t)) |
Вывод уравнения динамики для примера, представленного на рис. 2.20:
![]() – уравнение
динамики,
– уравнение
динамики,
или
в другой форме
![]() .
.
![]() – уравнение
динамики в операторной форме. При этом
и
– уравнение
динамики в операторной форме. При этом
и
![]() .
.
е) Интегро-дифференцирующее звено.
Звено принято называть интегро-дифференцирующим, если связь между входом и выходом звена определяется дифференциальным уравнением вида
|
(2.45) |
где
k
– коэффициент передачи, T1
и T2
– постоянные времени, при чем .
![]() .
При
.
При
![]() звено
превращается в безинерционное, а при
звено
превращается в безинерционное, а при
![]() – в инерционное
первого порядка.
– в инерционное
первого порядка.
Уравнение в операторной форме:
|
(2.46) |
Передаточная функция:
|
(2.47) |
Переходная характеристика.
Она определяется по формуле 1.15
.
D(p)=T2∙p+1;
![]() .
.
K(0)=k; D(0)=1.
Характеристическое
уравнение (T2∙p+1)=0
имеет корень
![]() .
Тогда
.
Тогда
![]() .
.
Первая
производная характеристического
полинома равна
![]() .
При p=p1
.
При p=p1
![]() .
.
Тогда

или окончательно
|
(2.48) |
График переходной характеристики интегро-дифференцирующего звена представлен на рис. 2.21.
|
|
а) |
б) |
Рис 2.21. График переходной характеристики интегро-дифференцирующего звена: а) преобладает свойство интегрирования; б) преобладает свойство дифференцирования |
|
Частотные характеристики:
- комплексная частотная функция:
|
(2.49) |
- амплитудно-частотная характеристика:

Окончательно получаем
|
(2.50) |
- фазочастотная характеристика:
![]() .
.
Окончательно получаем
|
(2.51) |
Графические представления частотных характеристик интегро-дифференцирующего звена, в котором преобладают свойства дифференцирующего звена, приведены на рис. 2.22.
|
а) |
|
б) |
|
в) |
Рис. 2.22. Графические представления частотных характеристик интегро-дифференцирующего звена, в котором преобладают свойства дифференцирующего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Графические представления частотных характеристик интегро-дифференцирующего звена, в котором преобладают свойства интегрирующего звена, приведены на рис. 2.23.
|
а) |
|
б) |
|
в) |
Рис. 2.23. Графические представления частотных характеристик интегро-дифференцирующего звена, в котором преобладают свойства интегрирующего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Примеры интегро-дифференцирующего звена представлены на рис. 2.24.
|
|
а). Режим дифференцирования (T1/T2>1)
|
б) Режим интегрирования (T1/T2<1)
|
Рис. 2.24. Примеры реализации интегро-дифференцирующего звена |
|
Вывод уравнения динамики для примера, представленного на рис. 2.24, а):
Uc(t)+
U2(t)
= U1(t).
Учитывая, что
![]() :
:
![]() или,
учитывая, что
или,
учитывая, что
![]() ,
получим
,
получим
![]() (*).
(*).
Продифференцируем обе части уравнения (*)
![]() – уравнение
динамики.
– уравнение
динамики.
![]() – уравнение
динамики в операторной форме.
– уравнение
динамики в операторной форме.
При
этом
,
![]() и
и
![]() .
.
Вывод уравнения динамики для примера, представленного на рис. 2.24, б), сделать самостоятельно.
ж). Запаздывающее звено.
Звено принято называть запаздывающим, если связь между входом и выходом звена определяется дифференциальным уравнением вида
|
(2.52) |
где – время запаздывания.
Уравнение в операторной форме:
|
(2.53) |
Передаточная функция:
|
(2.54) |
Переходная характеристика:
|
(2.55) |
График переходной характеристики запаздывающего звена представлен на рис. 2.25.
|
Рис 2.25. График переходной характеристики запаздывающего звена |
Частотные характеристики:
- комплексная частотная функция:
|
(2.56) |
- амплитудно-частотная характеристика:
|
(2.57) |
- фазочастотная характеристика:
|
(2.58) |
Графические представления частотных характеристик запаздывающего звена приведены на рис. 2.26.
|
а) |
|
б) |
|
в) |
Рис. 2.26. Графические представления частотных характеристик запаздывающего звена: а) амплитудно-фазовая частотная характеристика; б) АЧХ; в) ФЧХ |
Примеры запаздывающего звена: длинный трубопровод (газопровод, паропровод), длинная электрическая линия без потерь, поточно–транспортные устройства (транспортеры).