Введение

Студентам, а также инженерам часто требуется решать задачи, которые связаны с численными методами: интегрирование функций, нахождение корня алгебраического уравнения, нахождение решения системы линейных уравнения.

Подобные задачи решаются с помощью численных методов, разработанных для решения математических задач при помощи вычислительной техники на таких языках программирования, как: QBASIC, TURBO PASCAL, C++, DELPHI, VISUAL BASIC и д.р. пакеты программ. В частности, математические пакеты MathCAD, Maple, MathLab также дают возможность решения подобных задач, а так же оптимизации технологического процесса.

Необходимо учитывать, что вычислительная техника не способна без погрешности записывать такие величины как и т.д., погрешность может появляться и при вычислении, округлении и других операциях.

В некоторых случаях при вычислении необходимо предварительно математически преобразовать или переписать в другом виде функции, это может существенно снизить погрешность или в ряде случаев без преобразования не сходятся решения.

С помощью вычислительной техники можно решить и иные инженерные задачи, но с определенной погрешностью.

1 Постановка задачи

1.1 Составить программу для решения методом золотого сечения.

1.2Составить программу для нахождение корня уравнения в точке методом Зейделя

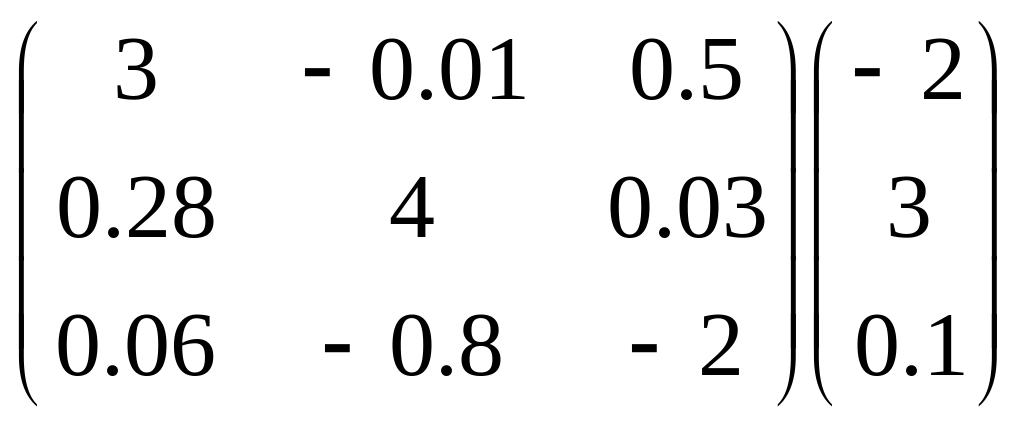
1.3 Составить программу для нахождения произведения вектора на число

2 Математическое описание методов

2.1 Метод золотого сечения

Метод золотого сечения применяется для поиска минимума функции одного переменного на отрезке. Метод использует следующее свойство непрерывных функций: если точки g и h (g < h) расположены на (a, b) и f(g) <= f(h), то на отрезке [a, h] есть хотя бы один минимум функции. Аналогично, если f(g) >= f(h), то на отрезке [g, b] есть хотя бы один минимум.

Метод золотого сечения выбирает на отрезке две симметричные точки: g = A+(B-A)*(3-Sqrt(5))/2 и h = A+(B-A)*(Sqrt(5)-1)/2. Применяется указанная выше процедура, приводящая к отрезку [A, h] или [g, B] (для определенности рассмотрим первый вариант). Если повторить указанную процедуру, то можно опять уменьшить отрезок. Важным свойством алгоритма является то, что на каждом шаге можно использовать одно значение функции из предыдущего шага, т.к. при новом разбиении отрезка [A, h] точками h' и g', мы увидим, что h' = g. Т.е. на каждом шаге вычисляется только одно значение функции (и ещё два в самом начале работы). Суть метода ясна из рисунка 1.

Рис. 1

Метод обладает стабильной линейной скоростью сходимости, не зависящей от рельефа функции [1].

2.2МЕТОД ЗЕЙДЕЛЯ

Метод Зейделя, иногда называемый методом Гаусса-Зейделя, является модификацией метода простой итерации. Последний может применяться для решения систем линейных уравнений вида

d₁₁x₁+d₁₂x₂+…+d_1nx_n+b₁=0

d₂₁x₁+d₂₂x₂+…+d_2nx_n+b₂=0 /1/

……………………………

d_n1­x₁+d_n2x₂+…+d_nnx_n+b_n=0

Приведём систему (1) к виду

x₁=a₁₁x₁+a₁₂x₂+…+a_1nx_n+b₁

x₂=a₂₁x₁+a₂₂x₂+…+a_2nx_n+b₂ /2/

…………………………….

x_n=a_n1x₁+a_n2x₂+…+a_nnx_n+b_n

, где a_ij=d_ij, i j, i, j=1, 2, 3,..., n, a_ii=d_ii+1,

или , где i=1,2,…,n, k=0,1,2,…,n.

Процесс итераций сходится независимо от выбора начального приближения, если выполняется одно из условий:

или , i=1,2,…,n /3/

Целесообразно за компоненты начального вектора x⁰={ } выбирать приближенные значения корней системы, находимые грубой прикидкой, или вектор b={b₁,b₂,b₃,…,b_n}.

Основная идея метода Зейделя заключается в том, что при вычис­лении к+1 -го приближения неизвестной x_i учитываются уже вычис­ленные ранее к+1 -е приближения неизвестных.

Пусть дана приведенная линейная система /2/. Выберем произ­вольно начальные приближения корней

.

Далее, предполагая, что к -е приближения корней известны, со­гласно методу Зейделя будем строить к+1 -е приближения корней по следующим формулам:

…………………………

………………………….

или , где i,k=1,2,…, n.

Указанные выше условия сходимости для метода простых итера­ций /3/ остаются верными для итерации по методу Зейделя.

Обычно метод Зейделя дает лучшую сходимость, чем метод про­стой итерации, однако возможны случаи, когда процесс Зейделя, сходится медленнее процесса итераций [3,4].

2.3УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

По определению, произведением вектора ={b₁; b₂;…; b_n} на число λ называется вектор {λ*b₁; λ*b₂;…; λ*b_n}. Для умножения вектора, то есть одномерного массива размерности n (b[1..n]), на число необходимо произвести n-ое количество вычислений [2].

Блок-схема программы GLAV

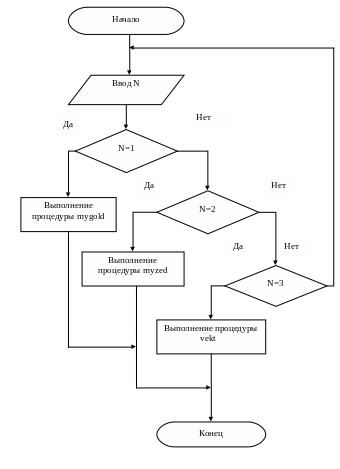
3.1Блок-схема модуля mygold1(процедура mugold)

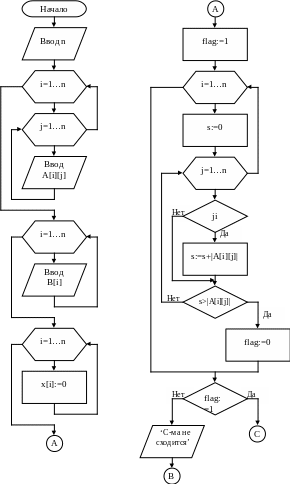
3.2 Блок-схема модуля muzed1 (процедура myzed)

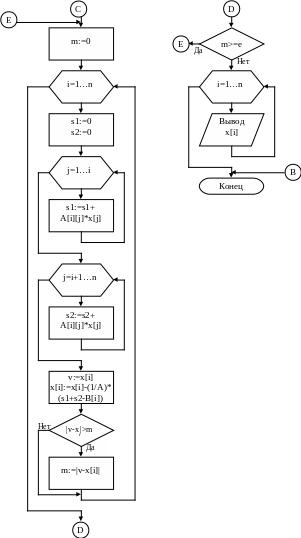
3. Блок-схема модуля mygold1 (функция vekt)

4 Описание стандартных процедур и функций

ClrScr – очищает экран.

Write – вывод значений на стандартное устройство (консоль) и в файл.

WriteLn – вывод значений на стандартное устройство (консоль) и в файл + перевод каретки.

Read – считать один или несколько символов после нажатия Enter.

ReadLn – считать один или несколько символов после нажатия Enter + перевод каретки.

ReadKey – считать один символ без нажатия Enter.

5 ОПИСАНИЕ НЕСТАНДАРТНЫХ ФУНКЦИЙ

MUGOLD- метод золотого сечения.

MUZED – метод Зейделя

VEKT– умножение вектора на число.