
- •010100 «Математика», 010500 «Прикладная математика и информатика, 010900 «Механика»
- •010101 «Математика», 010501 «Прикладная математика и информатика, 010901 «Механика»
- •1. Исследование положений равновесия нелинейной системы второго порядка
- •Задание 1
- •2. Производная в силу системы. Первые интегралы
- •Задание 2
- •3. Дифференциальные уравнения с частными производными первого порядка
- •Задача Коши для уравнения с частными производными
- •Задание 4
- •5. Исследование на устойчивость по первому приближению
- •Задание 5
- •6. Методы доказательства существования цикла
- •Принцип кольца
- •Задание 6
- •7. Метод Пуанкаре в теории нелинейных колебаний. Неавтономные уравнения.
- •Разложим функцию в ряд по степеням в окрестности точки
- •Если условия (7.12) выполнены, то порождающее уравнение имеет решение:
- •Будем искать решение последнего уравнения в виде
- •Исследуемое уравнение:
- •Метод Пуанкаре в теории нелинейных колебаний. Автономные уравнения
- •Отсутствие t в правой части приводит к усложнению задачи, так как период искомого решения оказывается неизвестным. Он будет, вообще говоря, зависеть от параметра .
- •Исследуемое уравнение:
- •Задание 7
Задание 2
Найдя
первый интеграл, изобразить фазовый
портрет уравнения на плоскости
![]() .
.
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17)
|
18)
|
19)
|
20)
|
21)
|
22)
|
23)
|
24)
|
25)
|
26)
|
27)
|
28)
|
29)
|
30)
|
31)
|
|
|
3. Дифференциальные уравнения с частными производными первого порядка
Линейным однородным дифференциальным уравнением первого порядка с частными производными называется уравнение вида
![]() ,
(1)
где
,
(1)
где
![]() –
заданные функции, определенные в
некоторой области
–
заданные функции, определенные в
некоторой области
![]() ,
а
,
а
![]() -
искомая функция.
-
искомая функция.
Линейным неоднородным уравнением первого порядка с частными производными называется уравнение вида
![]() ,
(2)
где
,
(2)
где
![]() –
заданные функции, определенные в
некоторой области
,
а
-
искомая функция.
–
заданные функции, определенные в
некоторой области
,
а
-
искомая функция.
Квазилинейным уравнением первого порядка с частными производными называется уравнение вида
![]() ,
(3)
где
,
(3)
где
![]() –
заданные функции, определенные в
некоторой области
–
заданные функции, определенные в
некоторой области
![]() ,
а
-
искомая функция.
,
а
-
искомая функция.
Очевидно, что уравнения (1) и (2) являются частным случаем уравнения (3), поэтому ниже ставятся задачи и рассматриваются методы решения квазилинейных уравнений (3). Результаты для уравнений вида (1) и (2) получаются как следствия из них.
Система
![]() обыкновенных дифференциальных уравнений
обыкновенных дифференциальных уравнений
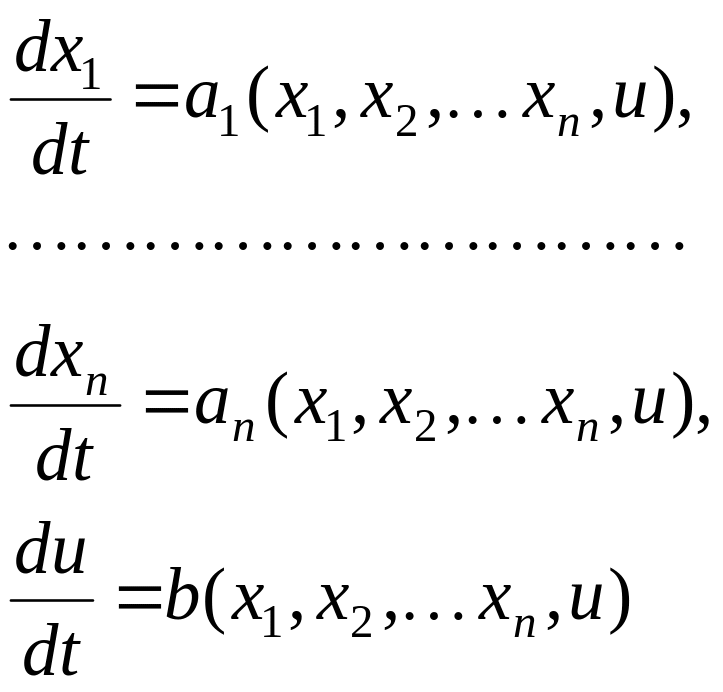 (4)
называется
системой
уравнений характеристик для
уравнения (3), а ее фазовые кривые
характеристиками
уравнения (3). Исключив параметр
(4)
называется
системой
уравнений характеристик для
уравнения (3), а ее фазовые кривые
характеристиками
уравнения (3). Исключив параметр
![]() из системы (4), получим систему уравнений
характеристик в симметричной форме
из системы (4), получим систему уравнений
характеристик в симметричной форме
![]()
![]() .
(5)
.
(5)
Пусть
найдено
![]() независимых первых интегралов
независимых первых интегралов
![]()
![]() (6)
системы
(5). Тогда общее решение уравнения (3) в
неявном виде определяется равенством
(6)
системы
(5). Тогда общее решение уравнения (3) в
неявном виде определяется равенством
![]() ,
(7)
где
,
(7)
где
![]() – произвольная дифференцируемая
функция.
– произвольная дифференцируемая
функция.
Если
функция
![]() входит только в один из первых интегралов
(6), например, в
входит только в один из первых интегралов
(6), например, в
![]() ,
то решение уравнения (3) может быть
записано в виде
,
то решение уравнения (3) может быть
записано в виде
![]() ,
где
,
где
![]() –
произвольная дифференцируемая функция.
Разрешив последнее уравнение относительно
,
получим общее решение в явном виде.
–
произвольная дифференцируемая функция.
Разрешив последнее уравнение относительно
,
получим общее решение в явном виде.
Точно также может быть найдено общее решение линейного неоднородного уравнения (2).
Общее решение линейного однородного уравнения (1) имеет вид
![]() ,
(8)
где
,
(8)
где
![]() –
независимые первые интегралы системы
уравнений характеристик, а
–
произвольная дифференцируемая функция.
–
независимые первые интегралы системы
уравнений характеристик, а
–
произвольная дифференцируемая функция.
Пример 1. Найти общее решение уравнения
![]() .
(9)
.
(9)
Решение.
Уравнение
(9) – линейное однородное уравнение.
Уравнение для характеристик в симметричной
форме имеет вид
![]() .
Найдем независимые первые интегралы
этого уравнения.
.
Найдем независимые первые интегралы
этого уравнения.
![]()
![]()
Согласно
формуле (8), общее решение уравнения (9)
имеет вид
![]() ,
где
,
где
![]() – произвольная дифференцируемая
функция.
– произвольная дифференцируемая
функция.
Пример 2. Найти общее решение уравнения
![]() .
(10)
.
(10)
Решение. Уравнение (10) – линейное неоднородное уравнение. Уравнение для характеристик в симметричной форме имеет вид
![]() .
(11)
.
(11)
Найдем
независимые первые интегралы этого
уравнения. Один первый интеграл находится
из уравнения
![]() и имеет вид
и имеет вид
![]() .
Для нахождения еще одного первого
интеграла применим прием, позволяющий
найти интегрируемую комбинацию.
Воспользуемся следующим утверждением:
если
.
Для нахождения еще одного первого
интеграла применим прием, позволяющий
найти интегрируемую комбинацию.
Воспользуемся следующим утверждением:
если
![]() ,
то при любых
,
то при любых
![]() справедливо равенство
справедливо равенство
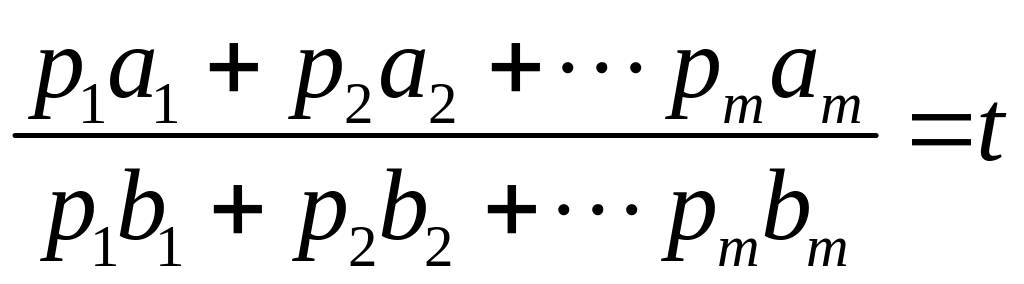 .
Используя это утверждение, из (11) получим
.
Используя это утверждение, из (11) получим
![]() .
Поскольку
функция
.
Поскольку
функция
![]() входит только в последний интеграл,
решение уравнения может быть записано
в виде
входит только в последний интеграл,
решение уравнения может быть записано
в виде
![]() или
или
![]() ,
где
,
где
![]() – произвольная дифференцируемая
функция.
– произвольная дифференцируемая
функция.
Пример 3. Найти общее решение уравнения
![]() .
(12)
.
(12)
Решение. Уравнение (12) – квазилинейное. Уравнение для характеристик в симметричной форме имеет вид
![]() .
(13)
.
(13)
Найдем
независимые первые интегралы этого
уравнения. Один первый интеграл находится
из уравнения
![]() и имеет вид
и имеет вид
![]() .
Для нахождения еще одного первого
интеграла применим описанный выше
прием, позволяющий найти интегрируемую
комбинацию. Из (13) последовательно
получаем
.
Для нахождения еще одного первого
интеграла применим описанный выше
прием, позволяющий найти интегрируемую
комбинацию. Из (13) последовательно
получаем
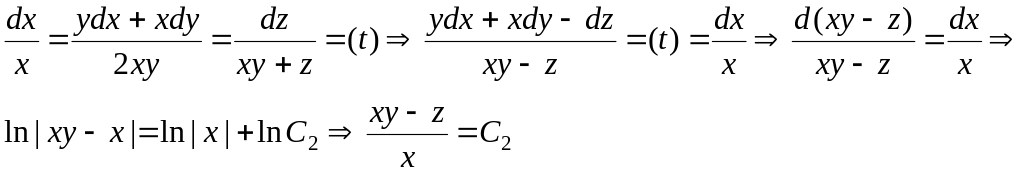
Согласно
формуле (7), общее решение уравнения (12)
в неявном виде определяется равенством
![]() ,
где
-
некоторая дифференцируемая функция.
Поскольку
входит только в один первый интеграл,
то решение мотет быть записано в виде
,
где
-
некоторая дифференцируемая функция.
Поскольку
входит только в один первый интеграл,
то решение мотет быть записано в виде
![]() ,
или, окончательно
,
или, окончательно
![]() ,
где
– некоторая дифференцируемая функция.
,
где
– некоторая дифференцируемая функция.
