
- •§ 5. Геометрические приложения определенных интегралов
- •Вычисление длины плоской кривой. Основные формулы
- •Задачи для самостоятельного решения
- •Вычисление объемов
- •§ 6. Приложения определенного интеграла в механике и физике Длина пути
- •Давление жидкости
- •Работа силы
- •Статические моменты и центр тяжести плоской фигуры.
- •Ответы и указания
- •ОглавлеНие
- •§ 5. Геометрические приложения определенных интегралов 120
- •Коллектив авторов решение задач по теме «интегральное исчисление функций одной переменной» Учебное пособие
§ 5. Геометрические приложения определенных интегралов
Вычисление площадей плоских фигур. Основные формулы. Если фигура на плоскости xOy ограничена прямыми x = a, x = b (a < b) и графиками функций y = (x), y = (x), причем (x) ≤ (x) (a ≤ x ≤ b), то ее площадь вычисляется по формуле
S
=
![]() .
.
В полярных координатах площадь сектора, ограниченного дугой кривой r = r() и лучами = и = ( ≤ ), вычисляется по формуле
![]() .
.
Если граница фигуры задана параметрическими уравнениями x = x(t), y = y(t), t (, ), то площадь фигуры вычисляется по одной из формул:
![]() ,
,
![]() ,
,
![]() ,
,
где и – значения параметра t, соответствующие началу и концу обхода контура в положительном направлении, при котором фигура остается слева.
Рассмотрим примеры.
Найти площадь фигуры, ограниченной линиями.
5.1.
y
=![]() ,
y=
,
y=![]() .
5.2.
y
=
tg x,
y
=
.
5.2.
y
=
tg x,
y
=![]() cos
x,
x
=
0.
cos
x,
x
=
0.
5.3.
y
=
2x2,
y
=
![]() .
5.4.
y =
ln(x
+ 6), y
=
3
ln
x,
y
=
0.
.
5.4.
y =
ln(x
+ 6), y
=
3
ln
x,
y
=
0.
5.5.
x
=
y2,
x
=![]() y2
+
1. 5.6.
y
=
2x–3
+
1, y
=
23-x
+
1, y
=
y2
+
1. 5.6.
y
=
2x–3
+
1, y
=
23-x
+
1, y
=![]() .
.
Решение.
5.1. Найдем точки пересечения графиков функций (рис. 2.1):
Рис. 2.1

x1 = – 4, x2 = 1.
Вычисляем площадь
![]() =
=
=
![]() =
=
=
![]() =
=
![]() .
.
5.2.
Найдем точку пересечения графиков
функций
![]() (рис. 2.2).
(рис. 2.2).
С
Рис.
2.2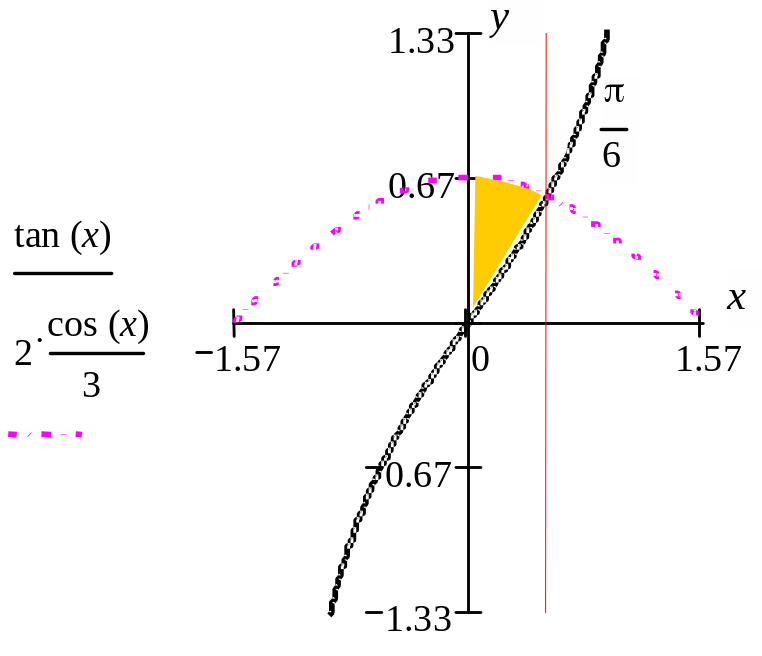
![]() z2=
z2=![]() .
Решение z
= – 2 постороннее. Решаем
далее, sin
x
=
.
Решение z
= – 2 постороннее. Решаем
далее, sin
x
=
![]() .
Находим площадь
.
Находим площадь
 =
=
= =
=
![]() .
.
5
рис.
2.3

2x2 = , x1 = 0, x2 = 6.
При 0 ≤
x
≤ 6 имеем
![]() ≤ ≤ 2x2.
Поэтому
≤ ≤ 2x2.
Поэтому
S
=
![]() =
=
= ![]() = 36.
= 36.
5.4. Ищем точку пересечения графиков функций (рис. 2.4):
ln(x + 6) = 3 ln x = ln x3, x + 6 = x3.
Я
Рис. 2.4

S
=
![]() +
+
![]() .
.
Интегралы вычисляем
с помощью формулы интегрирования по
частям. Для первого интеграла полагаем
u = ln(x
+ 6), du
=![]() ,
v
=
x;
для второго u
= ln(x
+
+ 6)
– 3 ln
x,
du
=
,
v
=
x;
для второго u
= ln(x
+
+ 6)
– 3 ln
x,
du
=
![]() ,
v
=
x.
,
v
=
x.
Получаем
![]() –
–
![]() +
+
![]() –
–
– ![]() = ln7 –
= ln7 –
![]() + 2ln8 – 6ln2 – ln7 –
+ 2ln8 – 6ln2 – ln7 –
– ![]() = – 1 + 6 ln7 – 6 ln6 +
= – 1 + 6 ln7 – 6 ln6 +![]() – 2 +
– 2 +
+ 6 ln 8 +
1 – 6 ln 7 + 3 =![]() + 1.
+ 1.
5
Рис. 2.5

![]() =
=
![]() =
=
=![]() =
=
![]() =
=
![]() .
.
При вычислении
интеграла по отрезку [–2, 2] мы учли
четность функции x
=
![]() .
.
5
Рис. 2.6

Найдем выражение
x
через y.
Получаем x1
=
![]() ,
x2
= =
,
x2
= = ![]() ,
,
![]() ≤ y
≤
2, так как точкой пересечения графиков
функций x1
=
и x2 =
=
будет точка (3, 2).
≤ y
≤
2, так как точкой пересечения графиков
функций x1
=
и x2 =
=
будет точка (3, 2).
Вычисляем площадь фигуры
S
= =
=
 .
.
Вычислим интеграл, применяя формулу интегрирования по частям, полагая
u
=
![]() ,
du =
,
du =![]() ,
v =
y – 1.
,
v =
y – 1.
Тогда
S
= – 2 =
=
 =
=
=
![]() =
=
![]() – 1 =
– 1 =
![]() .
.
5.7. Найти площадь фигуры (рис. 2.7), ограниченной параболой y = – x2 – 2x + 3, касательной к ней в точке М(2, – 5), и осью ординат.
Решение. Найдем уравнение касательной: y = – 2x– 2, y(2) = – 6. Тогда y + 5 = – 6(x – 2) – уравнение касательной, проходящей через точку М(2, – 5). Перепишем уравнение в виде y = – 6x + 7.
В
Рис. 2.7
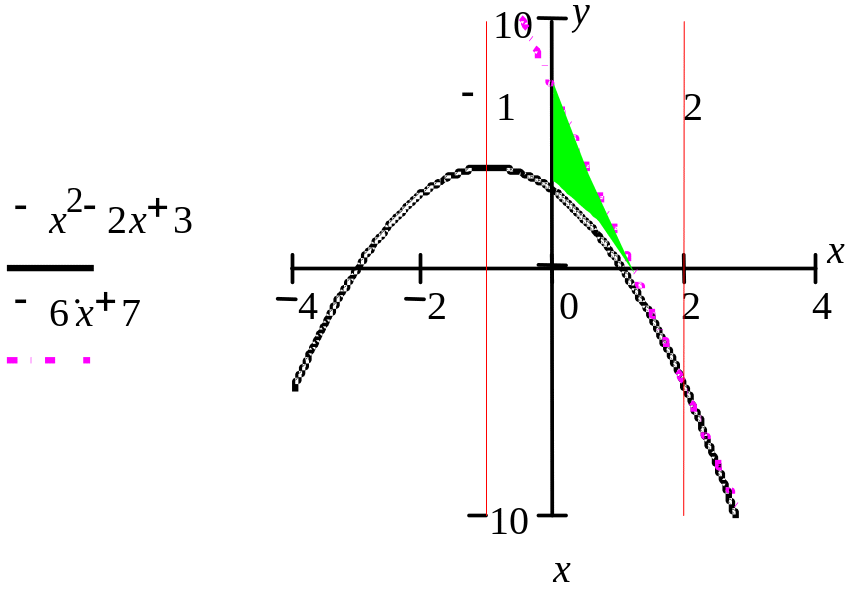
S
=
![]() =
=
=
![]() =
=
![]() =
=
![]() =
=
![]() =
.
=
.
Вычислить площади криволинейных трапеций, образованных графиками следующих функций.
5.8.
y
=![]() ,
x
[0, 1).
,
x
[0, 1).
5.9. y = х4e–x, x [0, ).
Решение.
5.8.
При x[0,1)
![]() ≥ 0 и, следовательно,
≥ 0 и, следовательно,
S
=
![]() =
=
 =
=
![]() =
=
=
 =
=![]() +
+
![]() = 2.
= 2.
Отметим, что в этом примере площадь вычислена с помощью несобственного интеграла.
5.9. Имеем
![]() .
.
Вычислим интеграл
с помощью формулы интегрирования по
частям, примененной несколько раз.
Воспользуемся обобщенной формулой
интегрирования по частям (см. гл. I,
§ 3). Положим u
=
x4.
Тогда u
= 4x3,
u
= 12x2,
u
= 24x,
![]() = 24. Далее v
= e-x,
v1
=
= 24. Далее v
= e-x,
v1
=
![]() = –
e–x,
v2
=
= –
e–x,
v2
=
![]() =
e–x,
v3
= –
e–x,
v4
=
e–x.
=
e–x,
v3
= –
e–x,
v4
=
e–x.
Получим
S
=
![]() =
=
![]() –
–
![]() –
–
![]() –
–
– ![]() +
+
![]() .
.
Поскольку
![]() ,
m
= 1, 2, … (это
доказывается последовательным применением
правила Лопиталя), то мы получаем
,
m
= 1, 2, … (это
доказывается последовательным применением
правила Лопиталя), то мы получаем
S
=
=
![]() = 24.
= 24.
Найти площадь фигуры, ограниченной кривыми, заданными в следующих полярных координатах.
5.10. r = a cos3, (a = 2).
5.11. r = 2 – cos , r = cos .
5.12.
r
=![]() ,
r
=
,
r
=![]() (внутри окружности).
(внутри окружности).
5.13. r = 2, = 0 (0 ≤ ≤ 2π).
5.14. r2 = 4 cos 2, r2 = 4 sin 2 (пересечение областей, ограниченных этими кривыми).
Решение.
5.10. Так как функция
r
= a
cos
3
имеет период T
=![]() ,
то при изменении
от 0 до 2π радиус-вектор описывает три
равных лепестка кривой (рис. 2.8). Допустимыми
для
являются те значения, при которых cos 3
≥ 0, откуда
,
то при изменении
от 0 до 2π радиус-вектор описывает три
равных лепестка кривой (рис. 2.8). Допустимыми
для
являются те значения, при которых cos 3
≥ 0, откуда
Рис. 2.8
![]()

![]() ,
,
k = 0, ±1, ±2, …
При k
= 0 имеем первый лепесток, соответствующий
–![]() ≤
≤
.
При k
= 1 получаем пределы для ,
соответствующие второму лепестку,
≤
≤
.
При k
= 1 получаем пределы для ,
соответствующие второму лепестку,
![]() ≤
≤
≤
≤![]() .
Если k
= 2, то третий лепесток линии соответствует
изменениям
:
.
Если k
= 2, то третий лепесток линии соответствует
изменениям
:
![]() ≤
≤
≤
≤
![]() .
В этих трех промежутках заключена
кривая, соответствующая изменению
от 0 до 2π (полный оборот). Если брать k
= 3, 4, … , то мы не получим новой линии, а
будем каждый раз проходить одну и ту же
линию.
.
В этих трех промежутках заключена
кривая, соответствующая изменению
от 0 до 2π (полный оборот). Если брать k
= 3, 4, … , то мы не получим новой линии, а
будем каждый раз проходить одну и ту же
линию.
Поскольку лепестки одинаковы, то достаточно найти площадь одного из них и затем утроить.
Имеем
S
=
 = 3a2
= 3a2 =
=
 =
=
=  =
=
![]() .
.
При вычислении интеграла мы учли четность функции cos23 .
5
Рис. 2.9

![]() в полярных координатах (рис. 2.9). Найдем
площадь фигуры между линией r
= 2 – cos
и окружностью. Ясно, что площадь фигуры
есть разность площадей, ограниченных
двумя линиями:
в полярных координатах (рис. 2.9). Найдем
площадь фигуры между линией r
= 2 – cos
и окружностью. Ясно, что площадь фигуры
есть разность площадей, ограниченных
двумя линиями:
S
= S1
– S2,
где S1
=
![]() ,
,
S2
=
 .
.
Вычисляем эти интегралы.
S1
=
![]() =
=
=
![]() =
=
![]() ,
,
S2
=
=
 =
=
 =
=
![]() .
.
Окончательно
получаем S
=
![]() =
=![]() .
.
При вычислении S2 мы использовали четность функции cos2 .
5.12. Найдем все значения , при которых cos 2 ≥ 0. Имеем
![]() ≤
≤
≤
≤![]() ,
k = 0, ±1, ±2,…
,
k = 0, ±1, ±2,…
П
Рис. 2.10

![]() ≤
≤
,
при k
= 1 :
≤
≤
,
при k
= 1 :
![]() ≤
≤
≤
≤![]() .
Далее при k
= 2, 3, … мы будем получать один из этих
двух лепестков (рис. 2.10). Итак, фигура
ограничена двумя одинаковыми лепестками.
Нас интересует площадь фигуры внутри
окружности r
=
.
.
Далее при k
= 2, 3, … мы будем получать один из этих
двух лепестков (рис. 2.10). Итак, фигура
ограничена двумя одинаковыми лепестками.
Нас интересует площадь фигуры внутри
окружности r
=
.
Найдем полярные
координаты точек пересечения кривой r
=
с окружностью r
=
.
Решая уравнение
=
,
получаем
= ±![]() ,
k
= 0, ±1, …
,
k
= 0, ±1, …
Выберем
значения
из
отрезка [–π,
π] такие,
что cos
2
≥ 0. Ясно, что достаточно рассмотреть
![]() =
=![]() ,
,
![]() =
,
что соответствует первому лепестку.
Вычислим соответствующую площадь и
удвоим ее, что даст нам искомую площадь.
Имеем
=
,
что соответствует первому лепестку.
Вычислим соответствующую площадь и
удвоим ее, что даст нам искомую площадь.
Имеем
S
=
 +
+
 =
=
![]() +
+
 =
+
=
+
![]() =
+ 4 – 2
=
+ 4 – 2![]() .
.
П
Рис. 2.11

5.13. Линия r = 2 – спираль, раскручивающаяся из начала координат O. Нам требуется определить площадь, ограниченную одним витком спирали и полярной осью.
Вычисляем площадь.
S
=
![]() =
=
![]() =
=
![]() .
.
5
Рис. 2.12

4 sin
2 = 4
cos 2,
=![]() ,
=
,
=![]() .
.
Луч
![]() делит часть нашей области в первом
квадранте пополам, луч
делит часть нашей области в первом
квадранте пополам, луч
![]() делает то же самое с частью области в
третьем квадранте. Достаточно найти
площадь общей части
делает то же самое с частью области в
третьем квадранте. Достаточно найти
площадь общей части
0 ≤ r ≤ , ≤ ≤
и умножить на четыре. Это и будет искомое решение. Вычисляем
S
=
 =
=
 = 4
= 4![]() =
=
=
![]() = 2(2 –
).
= 2(2 –
).
Перейдя к полярным координатам, найти площадь области, ограниченной кривыми (рис. 2.13 и 2.14).


Рис. 2.13 Рис. 2.14
5.15.
x2
+ y2
= 6x,
x2
+ y2
= 6y,
точка
![]() принадлежит области.
принадлежит области.
5.16. x2 + y2 = 9, x2 + y2 = 2 x, x + y = 0, x – y = 0,
x > 0, x2 + y2 ≤ 9.
Решение.
5.15. Линии являются окружностями (x – 3)2 + y2 = 9 и x2 + (y – 3)2 = 9. Пересечение кругов делится биссектрисой y = x первого квадранта на две равные половины. Найдем площадь одной, затем удвоим.
В полярных координатах x = r cos , y = r sin , уравнение x2 + y2 = 6x окружности принимает вид r = 6 cos , уравнение второй окружности имеет вид r = 6 sin .
Вычисляем площадь:
S
=
 = 18
= 18 =
=
 =
=
![]() (π
– 2).
(π
– 2).
5.16.
Перейдем к полярным координатам x
= r
cos
,
y
= r
sin
.
Тогда граница области будет задаваться
уравнениями r
= 3, r
= 2
cos ,
= –
![]() ,
=
.
,
=
.
Наша область – фигура, симметричная относительно полярной оси (оси Ox). Найдем площадь заштрихованной области и результат удвоим. Получим искомый ответ.
Полярные координаты точки пересечения окружностей находятся из уравнения
3 = 2
cos
, cos
=![]() ,
= ±
.
,
= ±
.
Вычисляем площадь:
 =
π
+ 6
=
π
+ 6 =
=
=
π + π + 3 =
=
![]() + 3
– 3
=
.
+ 3
– 3
=
.
Найти площадь фигуры, ограниченной кривой, заданной параметрически.
5.17. x = a cos t, y = b sin t.
5.18. x = 3 cos t, y = 3 sin 2t.
Решение.
5.17. Данная линия
есть эллипс
![]() +
+![]() = 1. Используя формулу для вычисления
площади, находим
= 1. Используя формулу для вычисления
площади, находим
![]() =
=
![]() =
=
= ![]() = π ab.
= π ab.
5.18. Выражая y через x, получаем
y
= ± 2x![]() .
.
П
Рис. 2.15

![]() x
≥ 0 и y
= 2x
≥
0.
x
≥ 0 и y
= 2x
≥
0.
Таким образом, при
изменении t
от 0
до π точка (x,
y)
описывает на плоскости xOy
замкнутую кривую, симметричную
относительно оси Ox.
При изменении t
от π до 2π
x
изменяется сначала от 0 до –3 (t
изменяется от π до
),
затем от –3 до 0
![]() .
Ордината y
= –2x
≥
0 при t
.
Ордината y
= –2x
≥
0 при t
![]() и y
= 2x
≤
0 – при t
и y
= 2x
≤
0 – при t
![]() ,
т. е. при изменении t
от π до 2π мы получаем снова замкнутую
кривую, симметричную первой кривой
относительно оси ординат.
,
т. е. при изменении t
от π до 2π мы получаем снова замкнутую
кривую, симметричную первой кривой
относительно оси ординат.
Мы найдем площадь
фигуры, соответствующей изменению t
от 0 до
![]() ,
а затем умножим результат на четыре.
Это и даст нам искомый ответ. Вычисляем
,
а затем умножим результат на четыре.
Это и даст нам искомый ответ. Вычисляем
S
=
 =
=
 =
=
 =
=
= =
=
 = 24.
= 24.
