9.6. Багатокрокова лінійна модель

Логіка міркувань, що дозволила перетворити двокрокову стохастичну модель лінійного програмування в математично еквівалентну їй звичайну лінійну оптимізаційну модель, може бути успішно застосована й у випадку багатокрокових задач.

Як і раніше, необхідно виходити з припущення, що можливо лише кінцеве число Q наборів значень для фігурують в моделі випадкових величин (або, іншими словами, кінцеве число станів). У реальній багатокроковій задачі значення Q може бути настільки великим, що рішення результуючої задачі лінійного програмування виявиться практично неможливим; тому метод аналізу, що викладається нижче, представляється корисним головним чином у зв’язку зі спробою глибше розібратися в особливостях організаційного управління в умовах невизначеності.

Однак у деяких (хоча й рідких) випадках багатокрокова модель виявляється практично застосовною при рішенні реальних задач.

Нехай детерміністський прототип задачі виглядає наступним чином:

Максимізувати (1)

при обмеженнях

(2)

(3)

Припустимо, що в стохастичному варіанті моделі , та є випадковими величинами. Зокрема, допустимо, що число можливих станів дорівнює Q. Позначимо ці стани через ( , , ). Нижче розглядається трикрокова процедура, що використовується при формулюванні відповідної задачі лінійного програмування. Пропонована процедура представлена у загальному вигляді й тому придатна для будь-яких багатокрокових моделей.

Але при розгляді конкретних задач цю процедуру нерідко удається редукувати. Ідея полягає в тому, щоб почати з формулювання задачі, в якій передбачається, що ще до моменту прийняття того або іншого управляючого рішення відомо, який з можливих Q результатів фактично мав місце. Якби таке припущення відповідало реальному стану речей, то в результаті ми отримали б Q альтернативних варіантів дій або правил, що у сукупності вичерпним чином визначили би стратегію поводження. Наступний крок полягає в урахуванні тієї обставини, що у момент ухвалення рішення щодо вибору значень деяких (за умовою задач – цілком конкретних) перемінних не усі випадкові величини насправді виявляються визначеними. Тому первісне формулювання задачі повинне бути видозмінене шляхом накладення додаткових обмежень, з яких повинно походити, що у відповідних правилах зазначені керовані перемінні не повинні розрізнятися за індексом q. Так, наприклад, у всіх Q правилах прийняття рішень значення всіх керованих перемінних першого кроку повинні збігатися. На заключному кроці шліфується форма представлення моделі, що отримана на другому кроці.

Приведемо більш докладний опис даного методу.

Крок 1. Розглядається формулювання задачі, що була би правильною, яка була можливість одержувати інформацію щодо значень усіх фігуруючих у моделі випадкових величин до того, як вибираються значення керованих перемінних х_j, а саме розглядається наступна задача:

Максимізувати (4)

при обмеженнях

(5)

(6)

де – значення , що відповідають результату ( , , ).

Крок 2. Враховується фактичний порядок надходження інформації; при цьому всякий раз, коли на момент ухвалення рішення фактичні результати для випадкових величин невідомі, відповідні не розрізняються за індексом q. Так, наприклад, якщо значення підлягає визначенню до того, як стануть відомими значення випадкових величин, що фігурують у задачі, то до обмежень (5) і (6) додається умова .

Крок 3. З урахуванням обмежень, прийнятих на другому кроці, виконується спрощення тих або інших співвідношень моделі. Наприклад, у випадку, якщо має місце додаткова умова, приведена вище (див. крок 2), то усюди заміняються на ; потім приводяться подібні члени і виключаються надлишкові рівняння.

Приклад календарного планування виробництва. Розглянемо фірму, що складає календарний план випуску продукції, у якому повинний бути визначений обсяг виробництва x_t для кожного відрізка t, де t = 1, 2, 3. Позначимо рівень попиту на відрізку t через D_t і припустимо, що незадоволена на відрізку t частина D_t цілком пропадає. Нехай i_t є рівень запасів наприкінці періоду t; допустимо, що на початку відрізка 1 запаси відсутні, а запаси наприкінці відрізка 3 знецінюються. Позначимо через c_t прибуток, одержувану від кожної одиниці продукції, випущеної на відрізку t й комерційно реалізованої до кінця планового періоду.

Покладемо c_t = r – e_t, де r – ринкова ціна одиниці продукції, a e_t – витрати, пов’язані з виробництвом одиниці продукції на відрізку t. Нехай збереження кожної одиниці продукції, що залишається складованою до кінця відрізка t, обходиться в h_t. Тоді у детерміністському варіанті задача формулюється наступним чином:

Максимізувати (7)

при обмеженнях

(товарний баланс наприкінці відрізка 1) (8)

(товарний баланс наприкінці відрізка 2), (9)

(товарний баланс наприкінці відрізка 3), (10)

(11)

де – обсяг незадоволеного попиту на відрізку t.

При відомих значеннях D_t рішення для моделі (8) – (11) є тривіальним: припустивши, що попит у період t варто задовольнити за рахунок продукції, котра випускається на відрізку k (k ≤ t) таким чином, щоб різниця була максимальною.

Припустимо тепер, що задача містить елементи невизначеності. Зокрема, допустимо, що D_t є випадкова величина. Які в цьому випадку оптимальні значення ? Щоб відповісти на це питання, необхідно мати додаткові дані про імовірнісний закон, що визначає поводження D_t, a також знати, в якій послідовності встановлюються індивідуальні рівні x_t і який порядок надходження інформації щодо попиту.

Допустимо, що значення D_t не залежать від вибору значень x_t. Крім того, припустимо, що D₁ може приймати тільки два різних значення. При фіксованому значенні D₁ число можливих значень D₂ приймемо рівним 2; іншими словами, існує чотири можливі значення D₂. Аналогічно допустимо, що для кожного можливого значення D₁ та D₂ існує два можливих значення D₃, тобто сумарне число можливих значень D₃ дорівнює 8. Коротше кажучи, рівні попиту D_t є залежними випадковими величинами, причому існує Q = 8 можливих станів (D₁, D₂, D₃), що позначимо через (D_q1, D_q2, D_q3), де q = 1, 2, ..., 8 (див. табл. 9.1).

Таблиця 9.1

Можливі значення D_t (t = 1, 2, 3)

D1	D2	D3	pq
D11 = D21 = D31 = D41	D12 = D22	D13	p1
		D23	p2
	D32 = D42	D33	p3
		D43	p4
D51 = D61 = D71 = D81	D52 = D52	D53	p5
		D63	p6
	D72 = D82	D73	p7
		D83	p8

Щоб з’ясувати, як відбиває на структурі моделі порядок надходження інформації щодо випадкових результатів, а також порядок проходження управляюючих рішень, розглянемо чотири різні ситуації.

Наявність повної прогностичної інформації. Припустимо, що фактичні значення усіх випадкових величин виявляються відомими до того, як вибирається значення кожної з керованих перемінних. У цьому випадку задача, описана у зв’язку з приведеним вище формулюванням кроку 1, зводиться до наступної задачі лінійного програмування:

Максимізувати (12)

при обмеженнях

, (13)

, (14)

, (15)

(16)

Дана модель містить 72 перемінні при 24 обмеженнях, кожне з яких має форму рівності. (Цілком очевидно, що для одержання чисельного рішення цієї задачі систему рівнянь (12) – (16) можна розкласти на 8 (Q = 8) автономних лінійних „програм”. Одержувані в результаті програми мають тривіальні рішення, оскільки вони мають структуру, що співпадає зі структурою детерміністичної моделі (7) – (11). Оптимальне значення цільовий функції (12) визначається як «середньозважене» на множині рішень автономних систем рівнянь за умови, якщо відповідні імовірності p_q задані).

Випадок, коли спочатку уточнюється попит, а потім приймається рішення. Припустимо, що до моменту ухвалення рішення відносно обсягу виробництва на відрізку t відомим є точне значення D_t, а також попередні рівні попиту. Тоді, відповідно до розглянутого вище кроку 2, необхідно ввести додаткові обмеження, зазначені в табл. 9.2. Так, наприклад, якщо , то обсяги виробництва на відрізку 1, запаси на кінець цього відрізка та обсяги нереалізованої продукції будуть однаковими для q = 1, 2, 3, 4.

Таблиця 9.2

Додаткові обмеження у випадку, коли спочатку уточнюється

попит, а потім приймається рішення

х11 = х21 = х31 = х41 і11 = і21 = і31 = і41 s11 = s21 = s31 = s41	x12 = x22 i12 = i22 s12 = s22
	x32 = x42 i32 = i42 s32 = s42
х51 = х61 = х71 = х81 i51 = i61 = i71 = i81 s51 = s61 = s71 = s81	x52 = x52 i52 = i52 s52 = s52
	x72 = x82 i72 = i82 s72 = s82

Аналогічно, , то обсяги виробництва, запаси та обсяги незадоволеного попиту для q = 3, 4 збігаються. Для реалізації кроку 3 виявляється зручним усі тотожні величини позначати тим самим символом; наприклад, замість х₂₁, х₃₁ та х₄₁ варто усюди підставити х₁₁ (аналогічна підстановка здійснюється для ( ). При цьому відразу ж виявляється, що обмеження (13) для q = 1, 2, 3, 4 цілком ідентичні, отже, досить розглянути лише одне з них.

Таким чином, у спрощеному виді задача містить перемінні

(17)

і включає обмеження (13) для q = 1, 5, обмеження (14) для q = 1, 3, 5, 7, обмеження (15) для q = 1, 2, ..., 8 та обмеження (16). У цілому в скороченій задачі фігурують 42 перемінні та 14 рівнянь, що задають обмеження.

Уточнення попиту після ухвалення рішення. Припустимо, що до моменту прийняття рішення відносно обсягу виробництва на відрізку t відомі лише попередні рівні попиту. Додаткові обмеження у цьому випадку (відповідно до кроку 2) представлені у табл. 9.3.

Таблиця 9.3

Додаткові обмеження у випадку, коли спочатку

приймається рішення, а потім уточнюється попит

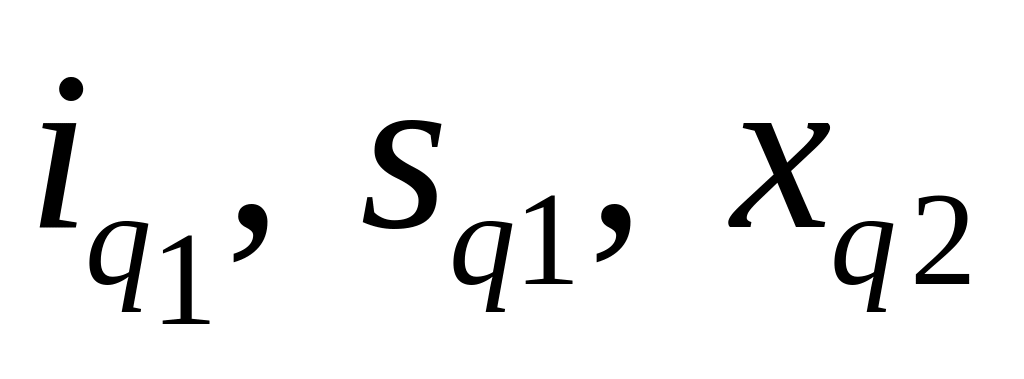
	і11 = ... = і41 s11 = ... = s41 х12 = ... = х42	і12 = і22 s12 = s22 x13 = x23
		і32 = і42 s32 = s42 x33 = x43
	і51 = ... = і81 s51 = ... = s81 х52 = ... = х82	і52 = і62 s52 = s62 x53 = x63
		і72 = і82 s72 = s82 x73 = x83

Помітимо, що при цьому перемінні x_q1 (q = 1, 2, ..., 8) не розрізняються за індексом q, оскільки рівень виробництва на відрізку 1 встановлюється до одержання яких-небудь точних даних щодо попиту. Відзначимо також, що обмеження на та накладаються при тих самих значеннях q, тому що рівні цих перемінних вибираються на основі однієї й тієї ж інформації, а саме з урахуванням відомого точно значення D₁.

Після спрощень, передбачених кроком 3, задача містить перемінні

(18)

і містить обмеження (13) при q = 1, 5, обмеження (14) при q = 1, 3, 5, 7, обмеження (15) при q = 1, 2, ..., 8 та обмеження (16). У цілому в скороченому варіанті моделі фігурують 35 перемінних при 14 обмеженнях, записаних у виді рівностей.

Випадок ухвалення рішення при повній відсутності даних про попит. Припустимо, нарешті, що обсяги виробництва для усього планового періоду повинні бути визначені до того, як стануть відомими значення D_t (хоча б для одного значення t = 1, 2, 3). Легко показати, що після належних спрощень у відповідній моделі будуть фігурувати перемінні

(19)

і ті ж обмеження, що й у випадку, коли спочатку приймається рішення, а потім уточнюється попит.