14.4. Область значений и ядро линейного оператора

Интерпретируя линейный оператор, действующий в линейном пространстве, как некоторое обобщение понятия функции, естественно возникает вопрос об области определения и области значений линейных операторов.

Под областью значений линейного оператора будем понимать множество образов всех элементов , то есть элементов вида . В этом случае, очевидно, что для любого линейного оператора его область определения совпадает с .

Ответ на вопрос “Что представляет собой область значений линейного оператора?” дает следующая теорема:

Теорема 14.5 Пусть – линейный оператор, действующий в линейном пространстве . Тогда

1. Множество элементов 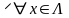есть подпространство в .

2. Если, кроме того, с базисом , то размерность этого подпространства равна .

Доказательство.

Пусть есть множество элементов вида и пусть . Тогда существуют и , такие, что и . По свойству линейности оператора имеем:

.

Аналогично и потому есть подпространство .

Пусть теперь с базисом . Поскольку каждый элемент есть линейная комбинация базисных элементов, то соответственно в силу линейности каждый элемент из области значений есть та же линейная комбинация элементов , то есть ^– линейная оболочка множества .

Выделим из множества максимальное подмножество линейно независимых элементов, и пусть число их оказалось равным k.

Тогда приходим к заключению, что размерность ^* есть k, и .

Теорема доказана.

Определение. Рангом линейного оператора в называется размерность его области значений. Ранг линейного оператора обозначается как .

Следствие. и не зависит от выбора базиса.

Следствие. Размерность области значений линейного оператора , действующего на некотором подпространстве линейного пространства , не превосходит .

Теорема 14.6 Ранг произведения линейных операторов и не превосходит ранга каждого из этих операторов.

Другой важной характеристикой линейного оператора является совокупность элементов линейного пространства , называемая ядром линейного оператора и обозначаемая .

Определение. Ядро линейного оператора состоит из элементов таких, что .

Теорема 14.5 Если и , то есть подпространство и .

Доказательство.

Пусть в базисе оператор имеет матрицу . По следствию для любого базиса. Тогда в координатной форме условие принадлежности некоторого элемента с

ядру оператора имеет вид

С другой стороны, поскольку каждое решение однородной системы линейных уравнений

является элементом ядра оператора , то размерность ядра есть максимальное число линейно независимых решений этой системы уравнений, которое равно

.

Теорема доказана.

14.5. Инвариантные подпространства и собственные векторы

Определение. Подпространство линейного пространства называется инвариантным подпространством линейного оператора , если для каждого элемента .

Пример 1. Множество радиусов-векторов точек некоторой прямой на плоскости , проходящей через начало координат, является инвариантным подпространством оператора поворота на угол  этих радиусов-векторов вокруг оси или оператора масштабирования – умножние на число λ (см. рис.).

z O  y x

Пример 2. Для оператора дифференцирования в линейном пространстве функций , имеющих на производную любого порядка, n-мерным инвариантным подпространством является линейная оболочка совокупности элементов вида ( ), где – различные константы.

Теорема 14.6 Матрица линейного оператора , заданного в линейном пространстве с базисом , тогда и только тогда имеет вид

,

когда линейная оболочка подмножества базисных элементов есть инвариантное подпространство оператора .

Доказательство.

Докажем достаточность. Пусть матрица оператора имеет указанный в формулировке теоремы вид. Тогда образ любой линейной комбинации элементов будет принадлежать их линейной оболочке, поскольку каждый столбец матрицы линейного оператора составлен из компонентов образа соответствующего базисного элемента.

Иначе говоря, если ,

то и

Откуда следует, что – подпространство. Достаточность доказана.

Докажем необходимость. Пусть есть инвариантное подпространство линейного оператора , являющееся линейной оболочкой подмножества базисных векторов . Тогда образ любого, в том числе и базисного, элемента, принадлежащего , также будет принадлежать . Это, в свою очередь, означает, что

что и доказывает необходимость.

Теорема доказана.

Задача. Показать, что всякое инвариантное подпространство невырожденного линейного оператора является также инвариантным подпространством оператора .

Решение. Пусть , где – инвариантное подпространство оператора , тогда, по условию задачи, .

Если оператор невырожденный, то для него существует обратный и связь элементов можно записать в виде , что и означает инвариантность подпространства относительно оператора .

В приложениях важную роль играют так называемые задачи "поиска собственных вектором и собственных значений", основой которых служит понятие одномерного инвариантного подпространства.

Определение. Ненулевой элемент называется собственным вектором линейного оператора , если существует число , такое, что . Число называется собственным значением оператора , соответствующим собственному вектору f.

Замечание. Согласно данному определению, является ненулевым элементом ядра линейного оператора , то есть .

Замечание. Допустим, что для некоторого линейного оператора , заданного в , удалось найти n линейно независимых собственных векторов . Это означает, что выполнены равенства

.

Приняв набор этих векторов за базис, можно заключить, что матрица линейного оператора в этом базисе будет иметь диагональный вид

,

для которого исследование свойств этого оператора существенно упрощается.

Задача. Показать, что, если линейный оператор имеет собственный вектор с соответствующим ему собственным значением , то элемент будет также являться собственным вектором линейного оператора с собственным значением .

Решение. По условию , но тогда в силу линейности оператора

.

Вычисление собственных векторов

и собственных значений линейного оператора

Выберем в некоторый базис , в котором разложение элемента будет , а линейный оператор имеет в этом базисе матрицу .

Равенство в координатной форме в имеет вид

или

(14.2)

Поскольку собственный вектор должен быть ненулевым по определению, то нас интересуют только нетривиальные решения системы (8.5.1), необходимым условием существования которых, согласно следствию 6.7.2, является равенство нулю определителя основной матрицы системы (8.5.1). Таким образом, мы приходим к условию, которому должны удовлетворять собственные значения данного линейного оператора

или же

(14.3)

Определение. Уравнение называется характеристическим уравнением, а определитель – характеристическим многочленом оператора , действующего в

Теорема 14.7 Характеристический многочлен линейного оператора не зависит от выбора базиса в .

Доказательство.

Заметим, что оператор , очевидно, линейный в силу линейности операторов и . Тогда, согласно следствию из теоремы 14.4, определитель его матрицы не меняется при замене базиса. Поэтому при переходе от базиса к базису имеем:

Теорема доказана.

Характеристическое уравнение является алгебраическим уравнением n-й степени относительно , что следует из определения детерминанта и формулы (14.3).

Решив характеристическое уравнение (14.3), из однородной системы уравнений (14.2) можно найти собственные векторы, соответствующие последовательно подставляемым в основную матрицу этой системы найденным собственным значениям.