14.3. Координатное представление линейных операторов
Пусть
в
заданы
базис
и линейный оператор
являющийся отображением
в
с базисом
.
Мы знаем, что
существует единственное разложение
,
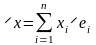то есть
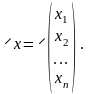
Аналогично
в
существует единственное разложение
для
,
и для которого, в силу линейности
справедливо представление вида
.
Приняв во внимание возможность и единственность в разложения
,
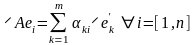с одной стороны, получаем, что
.
С другой стороны, если
является координатным представлением, то имеет место равенство
.
Наконец, в силу единственности разложения элемента конечномерного пространства по базису получаем
.
Данные
соотношения позволяют находить
координатное представление образов
элементов линейного пространства по
координатному представлению прообраза.
При этом отметим, что каждый линейный
оператор вида
в паре конкретных базисов полностью и
однозначно описывается матрицей размера
с элементами
.
Определение. Матрица
размера
,
столбцы которой образованы компонентами
элементов
:
называется
матрицей
линейного оператора
в базисах
и
.
В матричной форме соотношения имеют вид
(14.1)
в чем легко убедиться воспользовавшись их двухиндексной формой записи:
.
Полученный результат можно выразить следующим образом.
Теорема 14.3 Между множеством всех линейных операторов вида и множеством всех матриц размера имеется взаимно однозначное соответствие.
Доказательство.
Выше было показано, что каждому линейному оператору для конкретной пары базисов можно сопоставить матрицу размера . С другой стороны, соотношение
может быть принято за определение некоторого оператора вида , линейность которого следует из правил операций с матрицами.
Теорема доказана.
Действия с линейными операторами в матричной форме
Будем
рассматривать далее операторы вида
,
то есть линейные преобразования,
действующие в
с базисом
,
матрица которых квадратная, порядка
.
Введенные операции с матрицами позволяют
описать в конкретном базисе действия
с линейными операторами в следующей
форме.
Сравнение операторов:
.
Условие
означает, что
.
Сложение операторов:
.
Это
условие означает, что
.
Умножение оператора на число:
.
Это
условие означает, что
.
Произведение операторов:
.
Обращение операторов:
,
где
– единичный оператор (матрица).
Изменение матрицы линейного оператора при замене базиса
Выясним,
как меняется
– матрица линейного отображения
при замене базисов. Пусть в
даны два базиса
и
,
связанные матрицей перехода S,
а в
– два базиса
и
,
с матрицей перехода
Найдем соотношение связывающее матрицы
линейного отображения
и
.
Теорема 14.4 Матрица линейного оператора в базисах и связана с матрицей этого же оператора в базисах и соотношением
.
Доказательство.
При
переходе от базиса
к базису
компоненты элементов
– прообраза, и
– образа при действии оператора
,
в
этих базисах связаны равенствами
и
,
где
,
а
.
При этом в рассматриваемых базисах образы и прообразы элементов связаны соотношениями
и
,
но поскольку матрица перехода имеет обратную, то из этих соотношений последовательно получаем
Наконец, приходим к равенству
,
из
которого в силу произвольности вектора
следует утверждение теоремы.
Теорема доказана.
Следствие. Матрица линейного преобразования при переходе от базиса к базису в изменяется по правилу
.
Следствие. Определитель матрицы линейного преобразования не зависит от выбора базиса в .
Доказательство.
Из теоремы 14.4 следует
,
но поскольку
и
,
а
то окончательно получаем, что
.
Следствие доказано.
Замечание. В силу теоремы 14.4 в любом базисе нулевой оператор будет иметь нулевую матрицу, а единичный оператор – единичную.