6.Задачи с функционалом, содержащим производные высших порядков

Рассмотрим функционал, содержащий производные высших порядков:

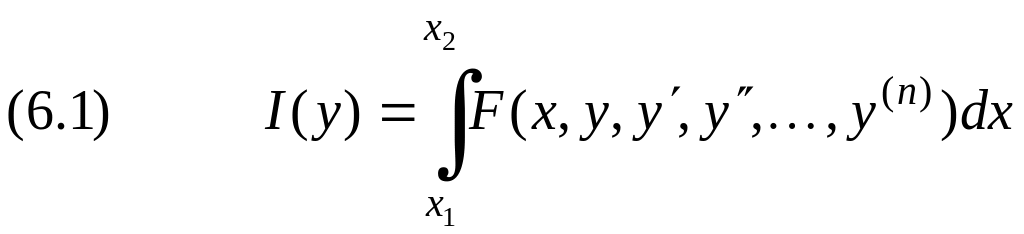
на функциях класса , т.е. имеющих непрерывную -ю производную на .

Граничные условия заданы в виде

Решение вариационной задачи заключается в нахождении функции, доставляющей экстремум функционалу (6.1) и удовлетворяющей на концах (6.2).

В отношении подынтегральной функции предполагается существование непрерывных по совокупности всех аргументов производных до -го порядка включительно. Такая вариационная задача называется задачей Лагранжа.

Решение вариационных задач, в которых функционал содержит производные высших порядков, может быть сведено к решению вариационной задачи с функционалом (5.1), т.е.

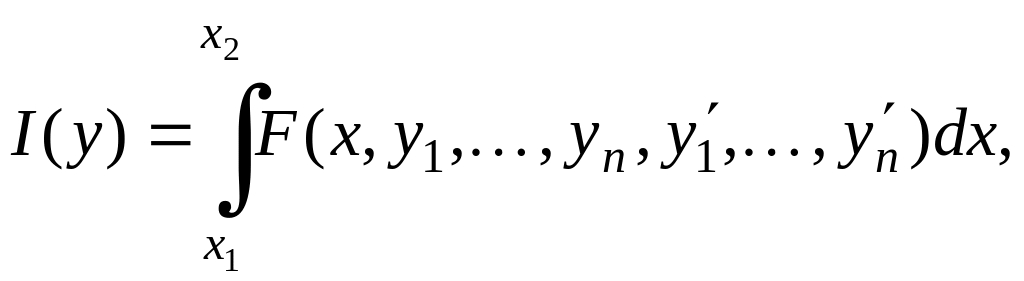
зависящим от нескольких функций, путём введения всех производных выше первого порядка в качестве новых независимых переменных, связав их друг с другом и с условиями

, ,..., .

Необходимые условия экстремума для вариационных задач с функционалом, зависящим от производных высших порядков, можно получить путём обобщения уравнения Эйлера.

Предположим, что функция доставляет экстремум функционалу (6.1) на однопараметрическом семействе функций , где - произвольная функция класса , , имеет вид

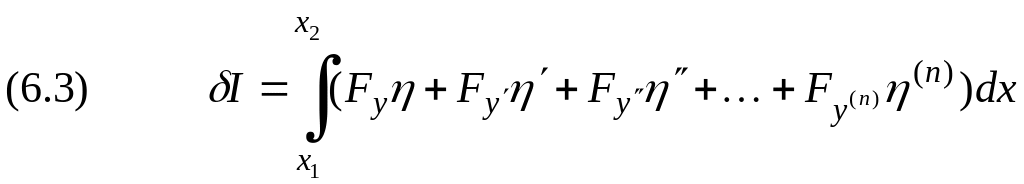а необходимым условием экстремума функционала является обращение в нуль первой вариации (6.3).

Если функция имеет производную порядка , то интегрирование по частям выражения (6.3) с учётом обращения в нуль первой вариации даёт необходимое условие экстремума в форме дифференциального уравнения Эйлера-Пуассона

Общее решение дифференциального уравнения Эйлера-Пуассона (6.4) содержит произвольных постоянных, которые можно определить из граничных условий (6.2).

В простейшей задаче вариационного исчисления условие Лежандра по знаку выражения позволяло отделять максимум функционала от минимума. В вариационных задачах с функционалом, который зависит от старших производных, условие Лежандра формулируется следующим образом.

Если доставляет минимум функционалу (6.1), т.е.

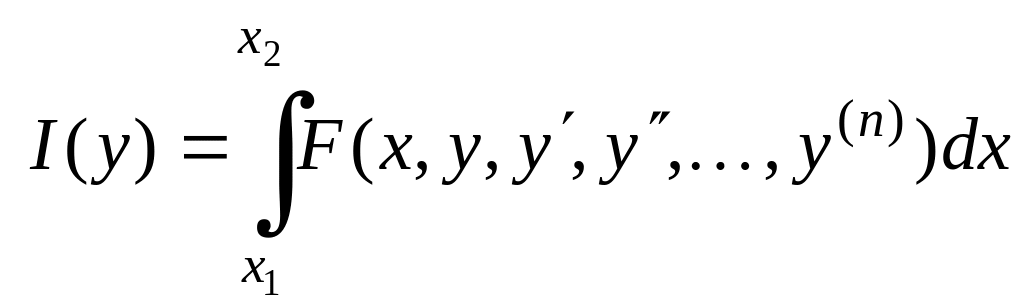то необходимо выполнение неравенства

а в случае максимума

Случай означает, что функционал – вырожденный.

В качестве примера вариационной задачи, функционал который содержит производные высших порядков, рассмотрим электродвигатель постоянного тока, который осуществляет перемещение исполнительного механизма. Известно, что нагрев якоря пропорционален квадрату тока. С другой стороны, ток якоря пропорционален сумме сил статического сопротивления исполнительного механизма и сил инерции, зависящих от ускорения, т.е.

где ток якоря; положение механизма; сила статического сопротивления, которую предполагаем постоянной; коэффициент, пропорциональный инерции приводимых в движение масс.