
- •664074, Иркутск, ул. Лермонтова, 83
- •1.Основные определения вариационного исчисления
- •2.Необходимые условия экстремума функционала
- •3.Вариационные задачи с подвижными концами
- •4.Ломаные экстремали
- •5.Функционалы, зависящие от нескольких функций
- •6.Задачи с функционалом, содержащим производные высших порядков
- •7.Условный экстремум
- •8.Каноническая форма уравнений эйлера
- •9.Оптимальное управление
- •10.Дифференциальные игры
- •11.Методы решения. Прямые методы
- •12.Методы решения. Метод множителей лагранжа
- •13.Методы решения. Принцип максимума
- •14.Методы решения. Динамическое программирование
12.Методы решения. Метод множителей лагранжа
Вариационные задачи на условный экстремум можно решать с помощью метода неопределенных множителей Лагранжа, применение которого сводит исходную задачу к задаче на безусловный экстремум.
Пусть, например, требуется исследовать на экстремум функционал
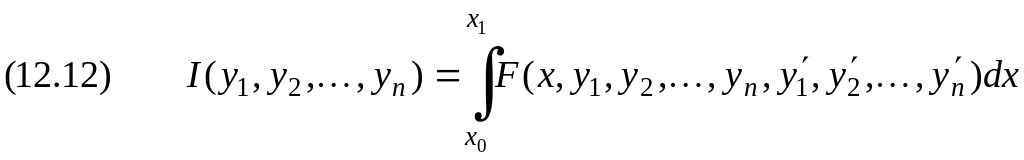
при наличии условий
![]()
Вместо исходной задачи (12.12), (12.13) составляют исходный функционал
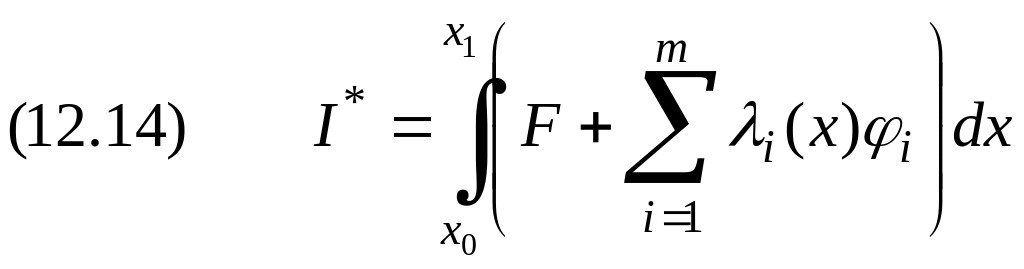 ,
,
где
![]() множители
Лагранжа, который исследуется на
безусловный экстремум. Обозначив
множители
Лагранжа, который исследуется на
безусловный экстремум. Обозначив
![]() ,
,
составляют систему уравнений Эйлера для нового функционала (12.14)
![]()
и дополняют систему (12.15) уравнениями связей (12.13).
Число
уравнений (12.13) и (12.15), равное
![]() ,
достаточно для определения
неизвестных функций
,
достаточно для определения
неизвестных функций
![]() и
и
![]() ,
а граничные условия
,
а граничные условия
![]() и
и
![]()
![]() ,
которые не должны противоречить
уравнениям связей, дают возможность
определить
произвольных постоянных в общем решении
системы уравнений Эйлера.
,
которые не должны противоречить
уравнениям связей, дают возможность
определить
произвольных постоянных в общем решении
системы уравнений Эйлера.
Метод множителей Лагранжа применим и в тех случаях, когда уравнения связей являются дифференциальными уравнениями
![]()
.
Проиллюстрируем применение метода множителей Лагранжа в частном случае минимизации функционала
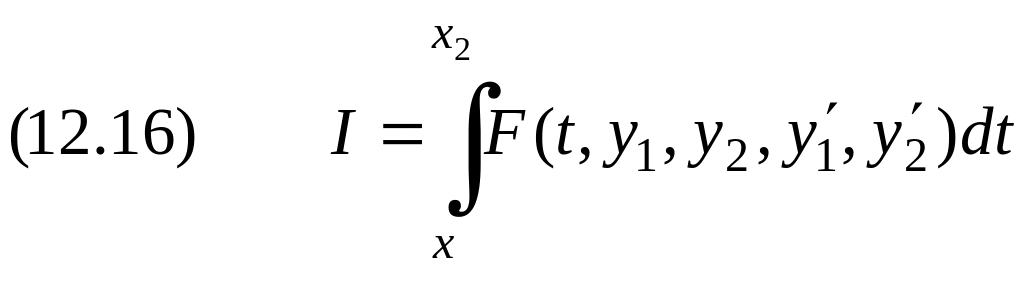
при условии
![]() ,
,
![]()
Необходимое условие функционала (12.17) определяется равенством нулю его первой вариации
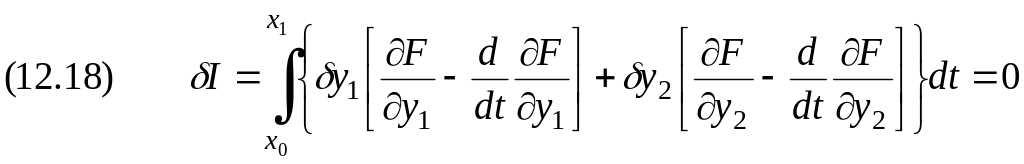 .
.
Наличие
условия (12.17) определяет зависимость
между
и
![]() .
Найдём вариацию (12.17), тогда
.
Найдём вариацию (12.17), тогда
![]() .
.
Умножим
(12.19) на множитель Лагранжа
![]() и проинтегрируем выражение (12.19)
и проинтегрируем выражение (12.19)
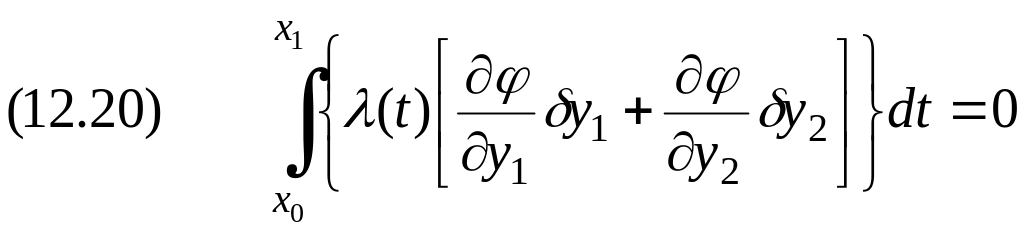 .
.
Сложим (12.18) и (12.20):
 .
.
Выберем
множитель Лагранжа
![]() таким образом, чтобы подынтегральное
выражение в первых скобках (12.21) было
равно нулю. Из этого следует, что
произвольной вариации
таким образом, чтобы подынтегральное
выражение в первых скобках (12.21) было
равно нулю. Из этого следует, что
произвольной вариации
![]() подынтегральное выражение во вторых
(12.21) также должно равняться нулю. Тогда
имеем уравнения Эйлера – Лагранжа
подынтегральное выражение во вторых
(12.21) также должно равняться нулю. Тогда
имеем уравнения Эйлера – Лагранжа
![]() ,
,
![]() ,
,
где
![]() ,
которые решаются совместно с условиями
(12.17).
,
которые решаются совместно с условиями
(12.17).
Рассмотрим
пример применения метода множителей
Лагранжа. Задано дифференциальное
уравнение системы
![]() ,
которое описывает поворот космического
аппарата в свободном пространстве под
действием управления
.
Требуется минимизировать функционал
,
которое описывает поворот космического
аппарата в свободном пространстве под
действием управления
.
Требуется минимизировать функционал
![]()
так, чтобы
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Введём
обозначение
![]() .
Тогда дифференциальное уравнение
системы примет вид
.
Тогда дифференциальное уравнение
системы примет вид
![]() ,
,
![]() .
.
Если
применить метод множителей Лагранжа,
рассматривая
в качестве переменной
![]() ,
то задача сводится к минимизации
функционала
,
то задача сводится к минимизации
функционала
![]() .
.
Уравнения
Эйлера-Лагранжа для данного примера
имеют вид
![]() ,
,
![]() ,
,
![]() .
.
Решение уравнения Эйлера-Лагранжа совместно с дифференциальными уравнениями системы и с учётом заданных граничных условий определяет оптимальное управление и оптимальные траектории системы в форме
![]() ;
;
![]() ;
;
![]() .
.
Методом множителей Лагранжа решаются задачи на условный экстремум в форме Лагранжа, Майера, Больца и изопериметрические задачи. В качестве примера рассмотрим применение метода множителей Лагранжа в изопериметрической задаче. Требуется найти экстремум функционала
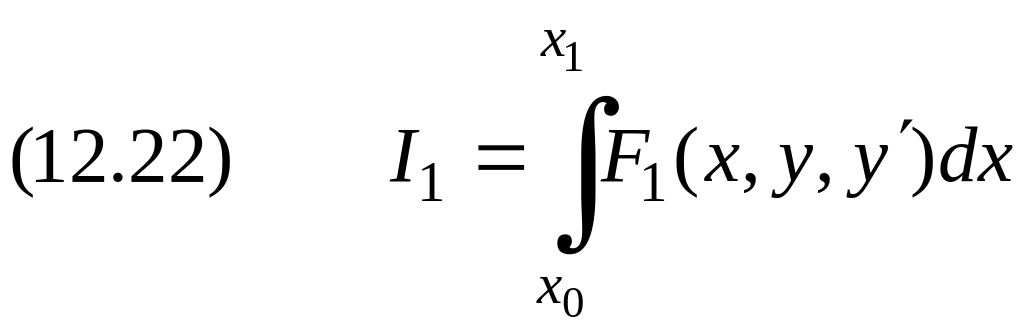
при условии, что другой функционал
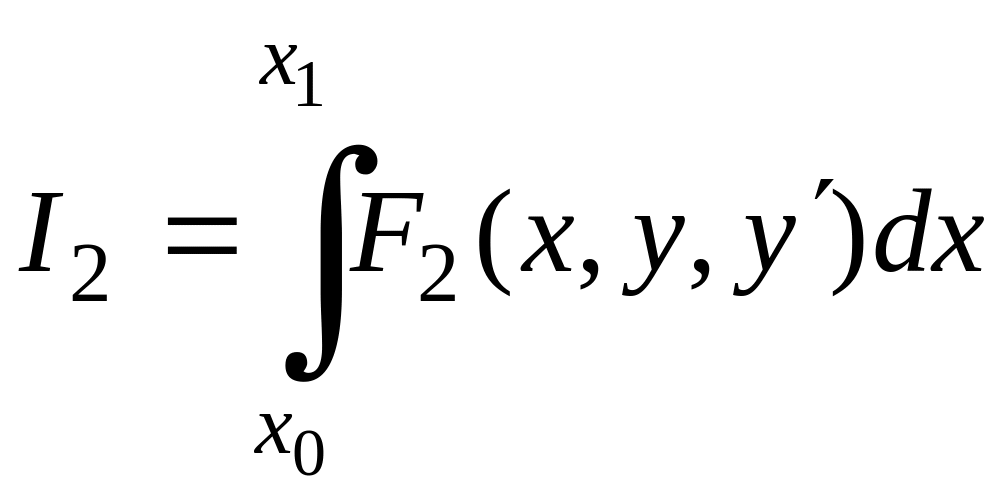
сохраняет заданное значение .
Сведём изопериметрическую задачу к общей задаче Лагранжа. Введя обозначение
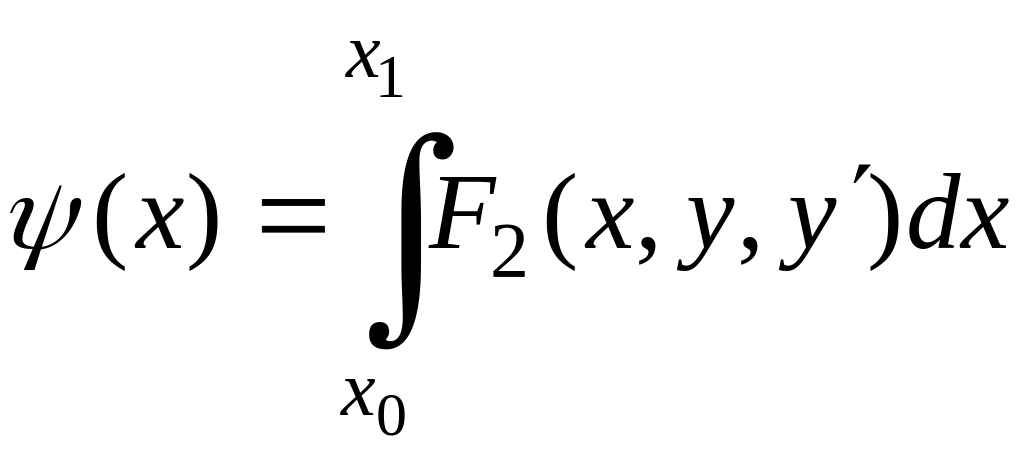 ,
,
получим
![]() .
.
Теперь
требуется найти функции
и
![]() ,
доставляющие экстремум функционалу
(12.22) при условии (12.23). Составляем новый
функционал
,
доставляющие экстремум функционалу
(12.22) при условии (12.23). Составляем новый
функционал
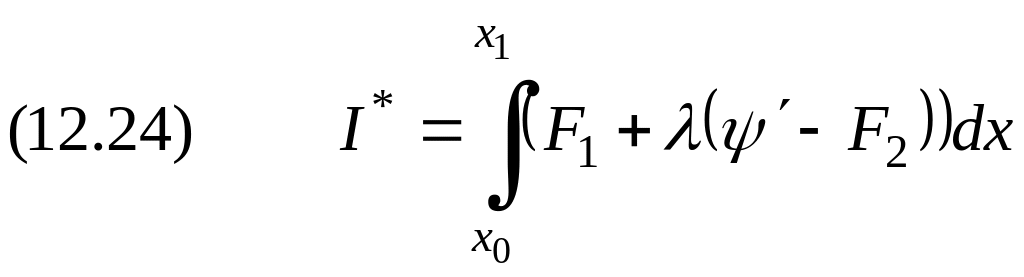 ,
,
где
![]() множитель
Лагранжа.
множитель
Лагранжа.
Уравнения Эйлера-Лагранжа для функционала (12.24) имеют вид
![]() ,
,
![]() ,
,
где
![]() .
Из второго уравнения следует
.
Из второго уравнения следует
![]()
или
![]() .
.
В изопериметрической задаче множитель Лагранжа является постоянным числом.
Р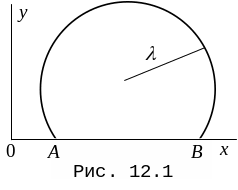 ешение
изопериметрической задачи методом
множителей Лагранжа проиллюстрируем
на следующем примере. Требуется найти
кривую заданной длины
ешение
изопериметрической задачи методом
множителей Лагранжа проиллюстрируем
на следующем примере. Требуется найти
кривую заданной длины
![]() ,
которая соединяет точки
и
и которая ограничивает совместно с
отрезком
наибольшую площадь (рис. 12.1). Выберем
систему прямоугольных координат таким
образом, чтобы ось абсцисс проходила
через точки
и
.
Тогда площадь, ограниченная искомой
кривой
,
определяется функционалом
,
которая соединяет точки
и
и которая ограничивает совместно с
отрезком
наибольшую площадь (рис. 12.1). Выберем
систему прямоугольных координат таким
образом, чтобы ось абсцисс проходила
через точки
и
.
Тогда площадь, ограниченная искомой
кривой
,
определяется функционалом
![]() .
.
Необходимо найти функцию , доставляющую максимум функционалу (12.25) при условии
![]()
и
![]() .
.
Будем считать, что
![]() .
.
Введём множитель Лагранжа и составим новый функционал
![]() .
.
Первый интеграл уравнения Эйлера-Лагранжа для функционала (12.26) имеет вид
![]() ,
,
где
![]() ;
;
![]() постоянная
интегрирования.
постоянная
интегрирования.
Из (12.27) следует
![]() ,
,
откуда
![]() .
.
Уравнение (12.28) представим в виде
![]() .
.
Интегрирование последнего уравнения даёт в качестве решения уравнение окружности радиуса
![]() .
.
Постоянные
![]() и множитель Лагранжа
определяются из условий прохождения
окружности через точки
и множитель Лагранжа
определяются из условий прохождения
окружности через точки
![]() и из условия равенства
длины окружности между
и
.
Наибольшая площадь ограничивается
прямой
и частью окружности радиуса
,
проходящей через точки
и
.
и из условия равенства
длины окружности между
и
.
Наибольшая площадь ограничивается
прямой
и частью окружности радиуса
,
проходящей через точки
и
.
