
- •Системы управления химико-технологическими процессами
- •1.1 Основные понятия управления
- •1.2 Характеристика производства
- •1.3 Задачи управления производством
- •2.1 Классификация автоматических систем управления
- •2.1.1 Основные определения
- •2.1.2 Основные типы
- •2.2 Характеристика и методика исследования
- •2.2.1 Математическое описание элементов
- •2.2.2 Частотные характеристики
- •2.2.3. Типовые звенья автоматических
- •2.2.4. Соединение звеньев
- •2.2.5 Устойчивость автоматических систем управления
- •2.2.6 Исследование аналоговых автоматических систем управления
- •2.1. Отимальные значения параметров настройки регуляторов для объектов с самовыравниванием
- •2.3 Нелинейные автоматические системы управления
- •2.4 Дискретные автоматические системы управления
- •2.5 Оптимальные автоматические системы управления
- •2.6 Адаптивные автоматические системы управления
- •Cистемы управления химико-технологическими процессами
2.2.2 Частотные характеристики
Комплексные числа. Комплексным числом называется выражение вида
![]() ,
(2.28)
,
(2.28)
где
![]() –
вещественная часть комплексного числа;
–
вещественная часть комплексного числа;
![]() –
мнимая часть комплекс-ного числа;
–
мнимая часть комплекс-ного числа;
![]() .
.
Если
![]() ,
то комплексное число называется чисто
мнимым. При
,
то комплексное число называется чисто
мнимым. При
![]() ком-плексное число становится вещественным.
Комплексные числа изображаются на
комплексной плоскости (рис.6).
ком-плексное число становится вещественным.
Комплексные числа изображаются на
комплексной плоскости (рис.6).
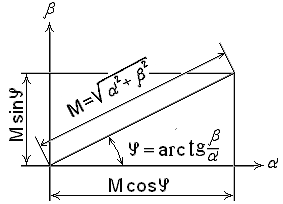
Рис. 6. Изображение комплексного числа на плоскости
Длина вектора М называется абсолютной величиной комплексного числа, или модулем
![]() .
(2.29)
.
(2.29)
Угол между
положительным направлением вещественной
оси и вектором
![]() называется
аргументом, или фазой
называется
аргументом, или фазой
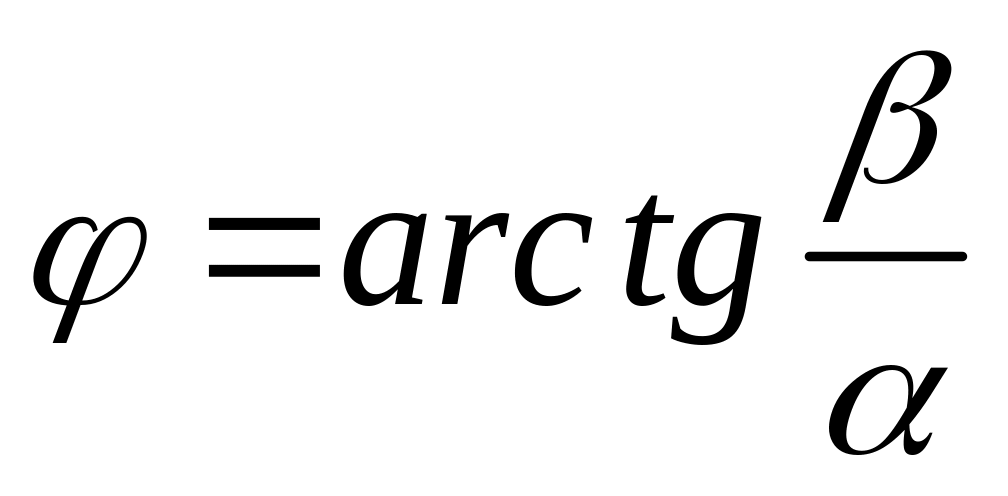 .
(2.30)
.
(2.30)
Абсцисса и ордината комплексного числа могут быть выражены так
![]() ,
(2.31)
,
(2.31)
![]() .
(2.32)
.
(2.32)
Отсюда
![]() .
(2.33)
.
(2.33)
По формуле Эйлера
![]() .
(2.34)
.
(2.34)
Поэтому
![]() ,
(2.35)
,
(2.35)
или
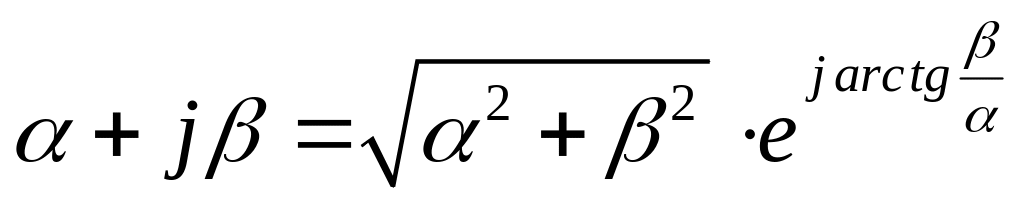 .
(2.36)
.
(2.36)
Операционное исчисление. Операционное исчисление служит для упрощения математических операций при расчётах, в частности при дифференцировании и ин-тегрировании. Решение уравнений операционным методом состоит из трёх этапов: приведение исходных уравнений к операторной форме; решение операторных уравнений; определение решений исходных уравнений по решениям операторных уравнений.
Для получения операторных уравнений, функции, входящие в уравнение, подвер-гаются прямому преобразованию Лапласа в соответствии с выражением
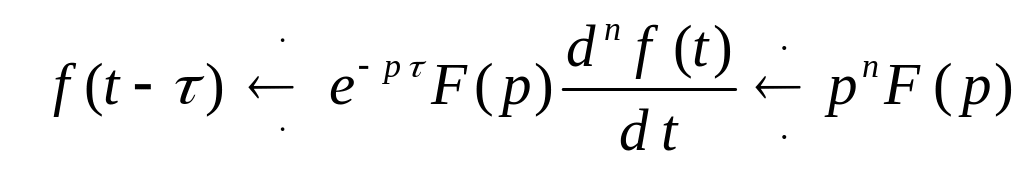 .
(2.37)
.
(2.37)
Функция f(t) вещественного переменного t, подвергаемая прямому преобразо-ванию Лапласа, называется оригиналом, а функция F(p) комплексного перемен-ного p, получаемая в результате преобразования, называется изображением.
Основными свойствами преобразования Лапласа являются:
а) линейность –
если
 , (2.38)
, (2.38)
то
 ;
;
б) интегрирование
оригинала –
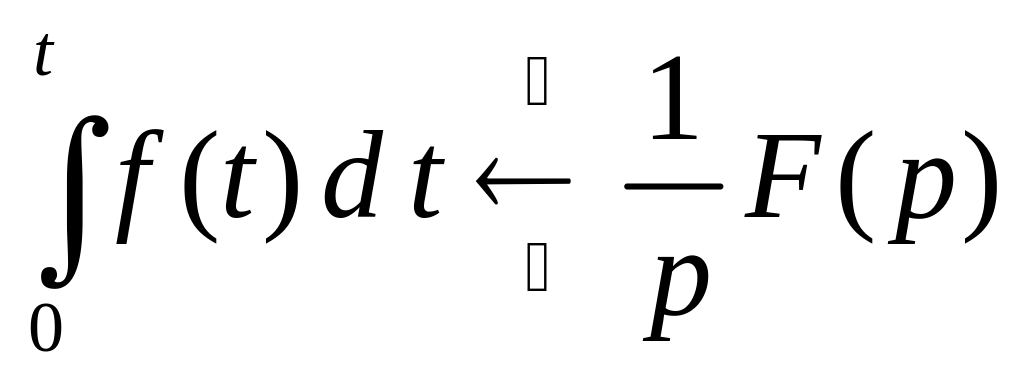 (2.39)
(2.39)
т.е. интегрированию оригинала соответствует деление изображения на оператор p;
в) дифференцирование
оригинала
–
 ,
(2.40)
,
(2.40)
т.е. дифференцированию оригинала соответствует умножение изображения на оператор p ;
г) дифференцирование
n
– кратное –
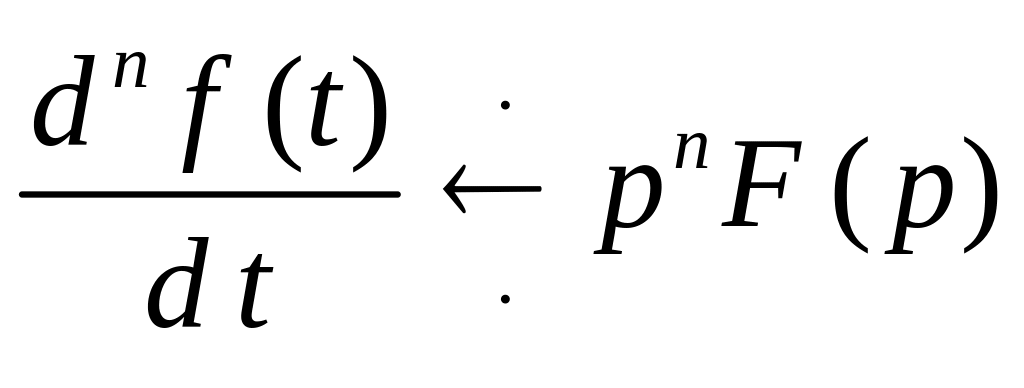 ;
(2.41)
;
(2.41)
д) запаздывание в области вещественного переменного –
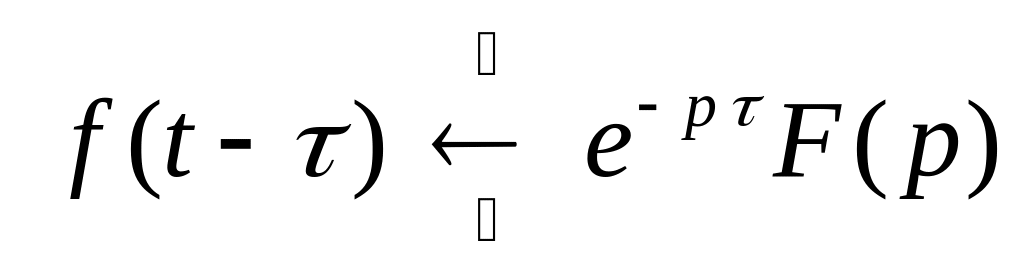 ,
(2.42)
,
(2.42)
т.е. сдвигу в
области вещественного переменного на
соответствует
умножение изображения на
![]() .
.
Далее из операторных уравнений определяется изображение решения поставлен-ной задачи. Чтобы отыскать решение исходных уравнений, необходимо совершить переход от изображения решения к его оригиналу. Этот переход возможен с по-мощью обратного преобразования Лапласа
 . (2.43)
. (2.43)
При вычислении преобразований Лапласа часто используют специальные табли-цы.
Передаточная функция. Передаточной функцией W(p) динамической систе-мы называется отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях
 .
(2.44)
.
(2.44)
Передаточная функция является одним из способов задания динамических харак-теристик САУ. Она однозначно связана с дифференциальным уравнением системы
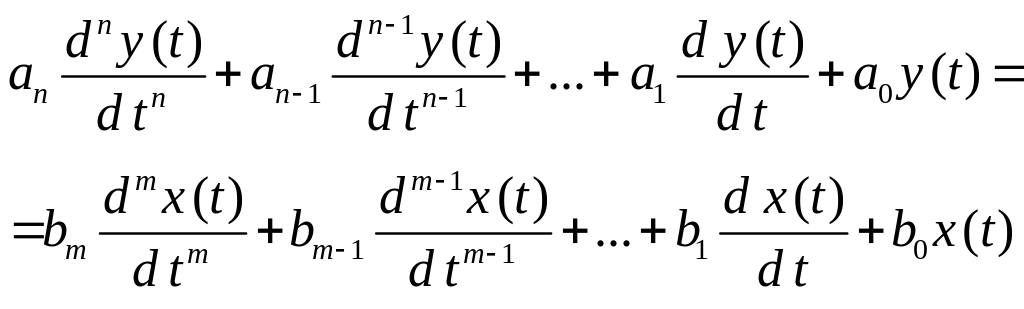 .
(2.45)
.
(2.45)
Дифференциальному уравнению (2.45) соответствует передаточная функция вида
 (2.46)
(2.46)
при
![]() .
.
Так, дифференциальному уравнению ёмкости (2.23) соответствует передаточная
функция
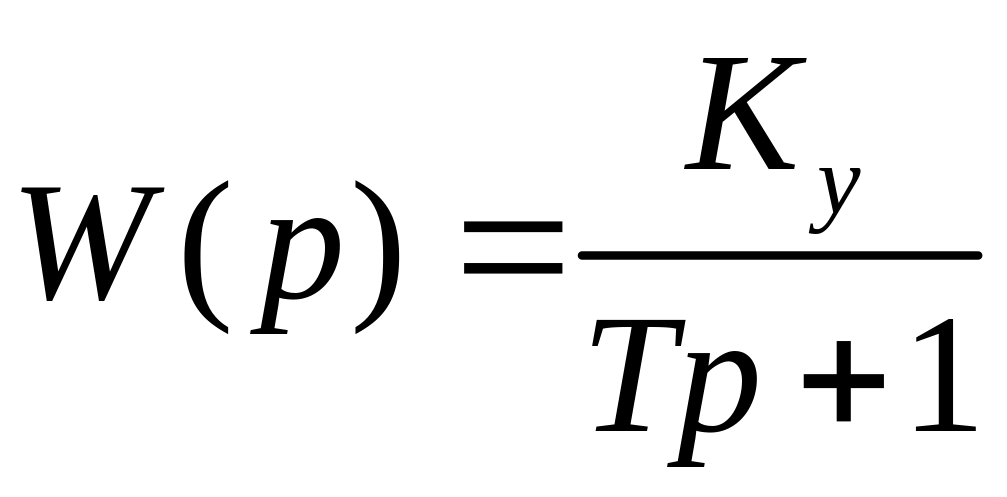 .
(2.47)
.
(2.47)
Передаточная функция связана с весовой функцией соотношением
![]() ,
(2.48)
,
(2.48)
т.е. передаточная функция есть изображение весовой функции.
Частотные характеристики. Частотные характеристики описывают установив-шиеся колебания на выходе звена, вызванные гармоническим воздействием на вхо-де. Если на вход звена подать гармоническое воздействие вида
![]() ,
,
то по окончании переходного процесса на выходе звена установятся колебания ви-да
![]() ,
,
т.е. отличающиеся от входных по амплитуде и фазе.
Амплитудной
частотной
характеристикой (АЧХ)
называется зависимость отно-шения
амплитуды гармонических колебаний на
выходе к амплитуде колебаний на входе
звена от частоты, т.е. зависимость вида
А(![]() ).
).
Фазовой
частотной характеристикой (ФЧХ)
называется зависимость разности фаз
между выходными и входными гармоническими
колебаниями от частоты этих колебаний,
т.е. зависимость вида
![]() (
).
(
).
АЧХ и ФЧХ можно объединить в одну характеристику – амплитудно-фазовую частотную характеристику (АФЧХ)
![]() .
(2.49)
.
(2.49)
Из уравнения (2.49) следует, что модуль АФЧХ представляет собой АЧХ, а аргумент – ФЧХ.
Аналитические
выражения для частотных характеристик
могут быть получены по передаточной
функции. Если в уравнении передаточной
функции (2.46)
положить
![]() , то получим АФЧХ
, то получим АФЧХ
 . (2.50)
. (2.50)
После освобождения от мнимости в знаменателе уравнение (2.50) можно запи-сать в виде
![]() .
(2.51)
.
(2.51)
Функция U( ) называется действительной (вещественной) частотной характе-ристикой, а V( ) – мнимой частотной характеристикой. Между частотными харак-теристиками существует связь
![]() (2.52)
(2.52)
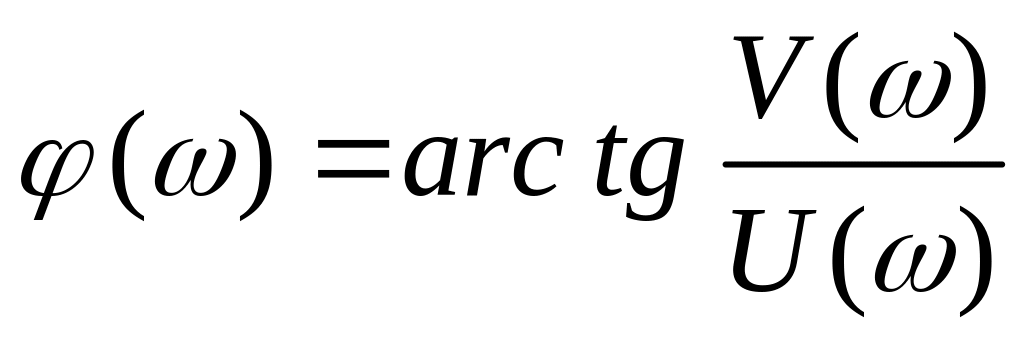 ;
(2.53)
;
(2.53)
![]() (2.54)
(2.54)
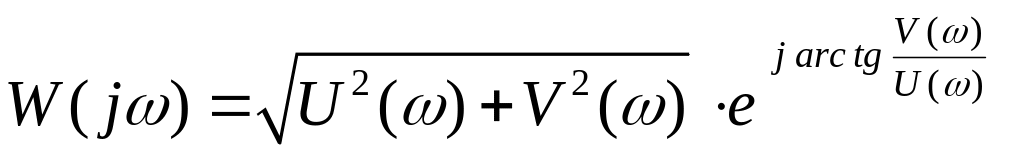 .
(2.55)
.
(2.55)
Если прологарифмировать выражение (2.49), то получим
. (2.56)
Примерный вид частотных характеристик приведён на рис. 7.
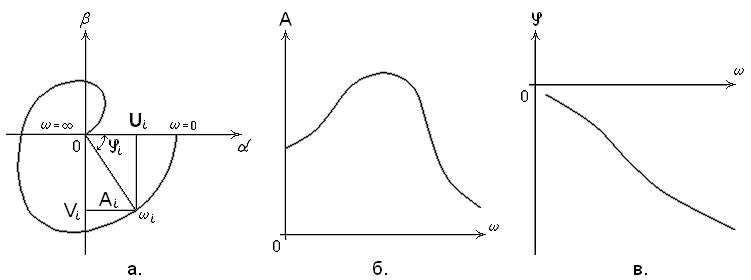
Рис.7. Частотные характеристики: а – АФЧХ ; б – ФЧХ ; в – АЧХ.
Зависимость L
= 20![]() lgA
от lg
называется
логарифмической амплитудной характеристикой
(ЛАХ),
а зависимость
от lg
– лагарифмической фазовой характеристикой
(ЛФХ).
lgA
от lg
называется
логарифмической амплитудной характеристикой
(ЛАХ),
а зависимость
от lg
– лагарифмической фазовой характеристикой
(ЛФХ).
В качестве единицы измерения L используется децибел, равный 0,1 бела.
Бел – это десятичный логарифм усиления мощности сигнала, т.е. 1 бел соответ-ствует усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т.д.
