Содержание отчета

1. Постановка задачи (с конкретизацией варианта).

2. Численное решение (с иллюстрацией таблиц вычислений).

3. Результаты вычислений.

4. График исследуемой функции.

5. Выводы

Вопросы и задания для самоконтроля

1. Описать процесс исследования функции и отделение корней. Привести пример.

2. Описать метод дихотомии уточнения корня. Привести пример.

3. Описать метод хорд и оценить его погрешность приближения. Привести пример.

4. Описать метод касательных и оценить его погрешность приближения. Привести пример.

5. Описать комбинированный метод уточнения корня и оценить его погрешность приближения. Привести пример.

6. Описать метод итераций уточнения корня и оценить его погрешность приближения. Привести пример.

Лабораторная работа № 2 Решение систем линейных уравнений

Цель работы: изучение численных методов линейной алгебры.

Содержание работы

1. Изучение численных методов:

• Гаусса,

• Гаусса с выбором главного элемента,

• Гаусса - Жордана,

• простых итераций,

• Зейделя.

2. Применение численных методов для решения систем линейных алгебраических уравнений.

Основные понятия

Все методы решения систем линейных уравнений ( СЛУ ) в основном делятся на две группы : точные и приближенные ( см. рис. 2.1 ).

приближенные

Методы решения

СЛУ

точные

число действий конечно	[бесконечный сходящийся процесс]
 метод Крамера  метод Гаусса . . .	 метод простых итераций  метод Зейделя . . .

Рис. 2.1

Замечание. Если в процессе вычислений неизбежны округления, то даже точные методы дают приближенные результаты.

Метод Крамера

- СЛУ

Правило Крамера: x_j = _j /  ,

где  - определитель системы;

_j - определитель, получаемый из определителя .

Замена

; .

j

Недостаток метода является трудоемким (т. е. требует выполнения очень большого количества операций) . Поэтому при решении СЛУ выше 3-го порядка не используется.

Метод Гаусса

Основная идея : последовательное исключение неизвестных, приводящее к построению эквивалентной системы с треугольной матрицей.

- СЛУ 4-го порядка

Прямой ход (определение коэффициентов эквивалентной системы).

Этап 1

Выбор ведущего элемента: а₁₁  0 .

Нормирование 1-го уравнения:

или

,

где ( j=2,3,4,5 ) .

Исключение неизвестной x₁

,

где (i = 2,3,4 ),

( j= 2,3,4,5 ) .

Все последующие этапы прямого хода осуществляются аналогично.

Этап 2

- ведущий элемент;

,

где 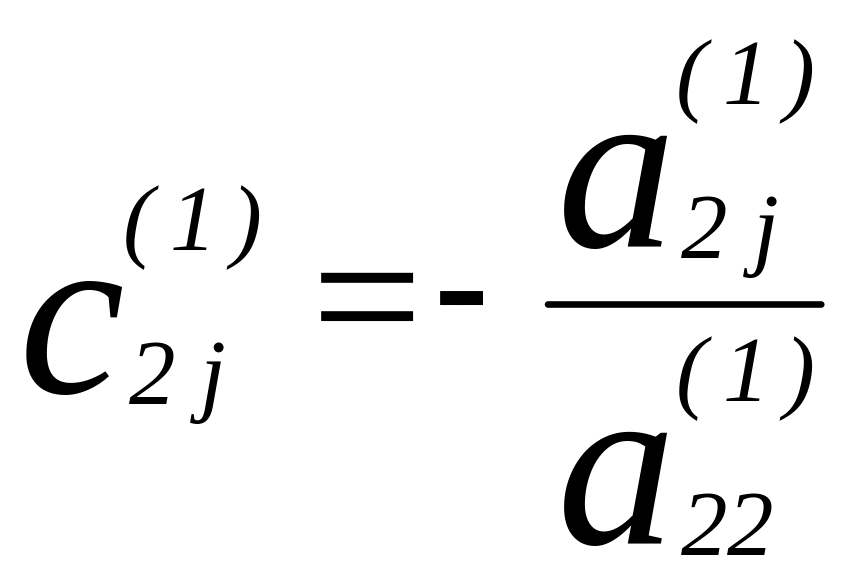( j = 3,4,5 ) ;

,

где (i = 3,4 ) ,

( j = 3,4,5 ) .

Этап 3

- ведущий элемент ;

,

где ( j = 4,5 ) ;

,

где ( i = 4 ),

( j = 4,5 ).

.

Обратный ход (определение неизвестных).

Объединение всех нормированных уравнений приводит к построению эквивалентной системы с треугольной матрицей:

Вычисления неизвестных ведется в обратной последовательности: x₄ , x₃ , x₂ , x₁ .

Необходимое и достаточное условие применения метода :

все ведущие элементы должны быть отличны от нуля: .

Пример. Решение методом Гаусса системы линейных уравнений

.