5. Метод Зейделя.
Метод
Зейделя - видоизменение МПИ (3) решения
СЛАУ, приведённых к виду (2), при котором
для подсчёта i-ой компоненты (k+1)-го
приближения к искомому вектору
используются уже найденные на этом,
т.е. (k+1)-ом шаге, новые значения первых
(i-1) компонент. Т.е если система (1) тем
или иным способом сведена к системе (2)
с матрицей коэффициентов
и вектором свободных членов
,
то приближения к её решению по методу
Зейделя определяются системой неравенств
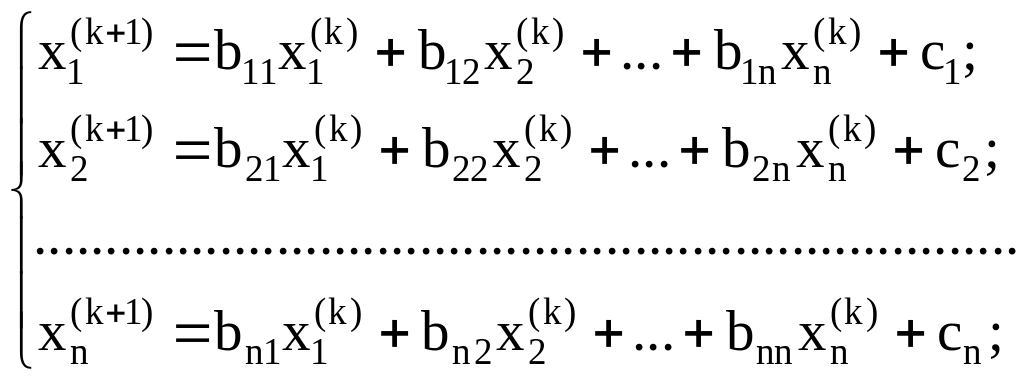
где
k=0,1,2,…, а
- компоненты заданного (выбранного)
начального вектора
.
Применительно к компьютерным расчётам один полный, т.е. векторный итерационный шаг метода Зейделя может интерпретироваться как реализация формулы (2), где под знаком равенства следует понимать знак присваивания, а под x – один и тот же линейный массив из n элементов, на нулевом шаге заполненный компонентами заданного начального вектора . Для компьютерной реализации одного шага метода простых итераций нужно целиком сохранять n-элементный массив x, подставляемый в правую часть, до тех пор, пока не сформируется полностью n-элементный массив – результат данного итерационного шага. В связи с такой интерпретацией метод Зейделя называют методом последовательных смещений, а метод простых итераций – одновременным смещением.
Практическая часть(листинг программы MatLab)
function zd
B=[142; 26; 23; 49];
A=[-83 27 -13 -11; 5 -68 13 24; 9 54 127 36;13 27 34 156];
n=4;
ep=0.0001
for k=1:n
e(k)=1;
h(k)=1/(A(k,k));
X(k,1)=0;
X(k,1)=0;
X_k(k,1)=0;
end
E=diag(e);
H=diag(h);
C=E-H*A;
D=H*B;
nor=norm(C,1);
if nor<1
for i=1:n
X(i)=0;
for j=1:n
X(i)=X(i)+C(i,j)*X(j);
end
X(i)=X(i)+D(i);
end
n1=max(abs(X-X_k));
k=1;
while n1 > (((1-nor)/nor)*ep)
X_k=X;
for i=1:n
X(i)=0;
for j=1:n
X(i)=X(i)+C(i,j)*X(j);
end
X(i)=X(i)+D(i);
end
n1=max(abs(X-X_k));
k=k+1;
end
disp('итераций'), k
else
disp('система не сходится')
end
Результат выполнения программы:
число итераций
i =
66
Данная система не решается последними двумя методами т.к.не все собственные числа матрицы меньше 1
A=[-83 27 -13 -11; 5 -68 13 24; 9 54 127 36;13 27 34 156];
eig(A)
ans =
-88.7036
-66.6865
184.0934
103.2968
Метод Якоби
Представим матрицу
системы (6.1) в виде
,
где
— диагональная, а
и
— соответственно
левая и правая строго треугольные (т.е.
с нулевой диагональю) матрицы. Тогда
система (6.1) может быть записана в виде
(6.7)
и если на диагонали исходной матрицы нет нулей, то эквивалентной (6.1) задачей вида (6.2) будет
, (6.8)
т.е. в равенствах (6.2) и (6.3) следует положить
Основанный на таком приведении системы (6.1) к виду (6.2) метод простых итераций (6.3) называют методом Якоби.
В векторно-матричных обозначениях он определяется формулой
(6.9)
Чтобы записать
метод Якоби (6.9) решения системы (6.1) в
развернутом виде, достаточно заметить,
что обратной матрицей к матрице
служит диагональная матрица
с элементами диагонали
.
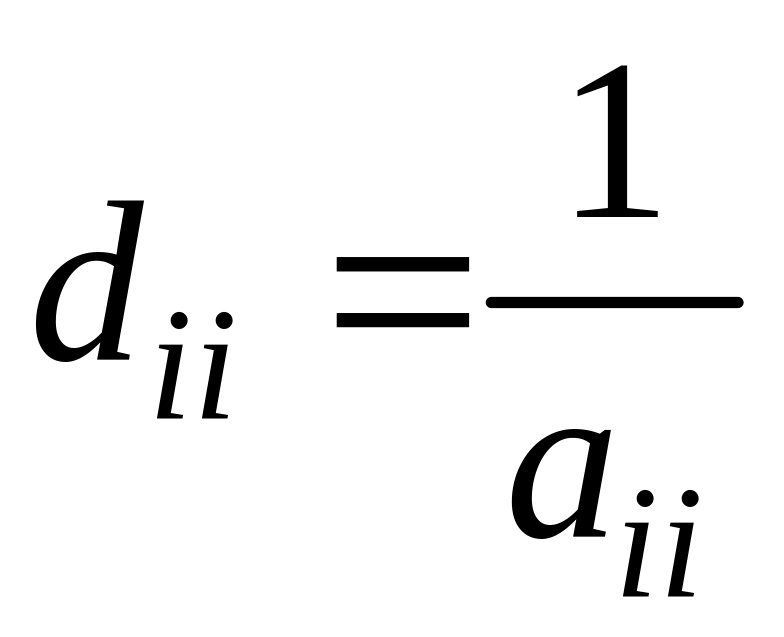Поэтому представление (6.8) системы (6.1),
записанной в виде (6.7), равнозначно
выражению «диагональных неизвестных»
через остальные:
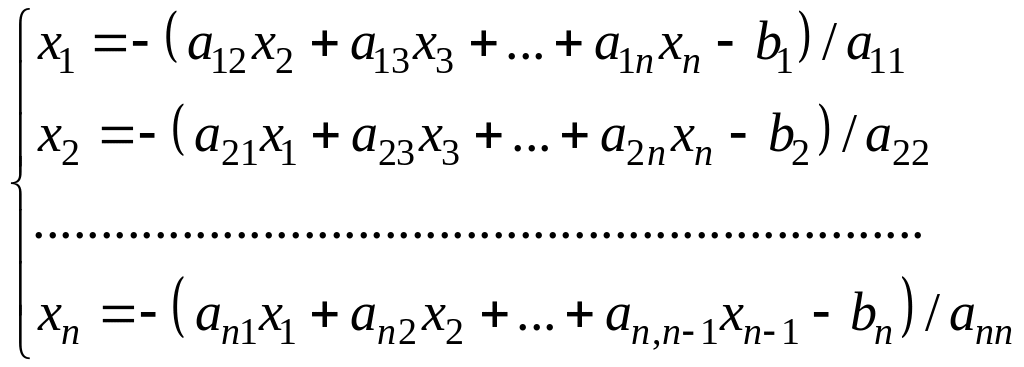(6.10)
При этом итерационный процесс имеет вид
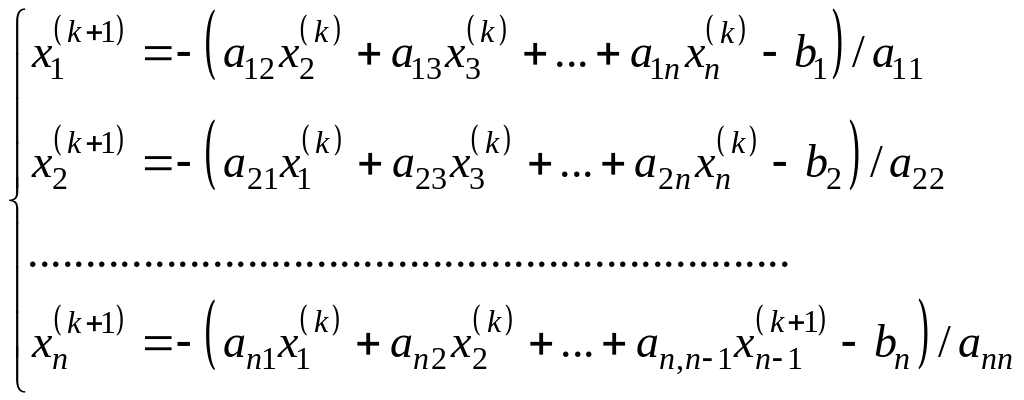(6.9а)
Теорема 6.3. В случае диагонального преобладания в матрице системы (6.1) метод Якоби (6.9) сходится.
Теорема 6.4. Метод Якоби (6.9) сходится к решению системы (6.1) в том и только том случае, когда все корни уравнения
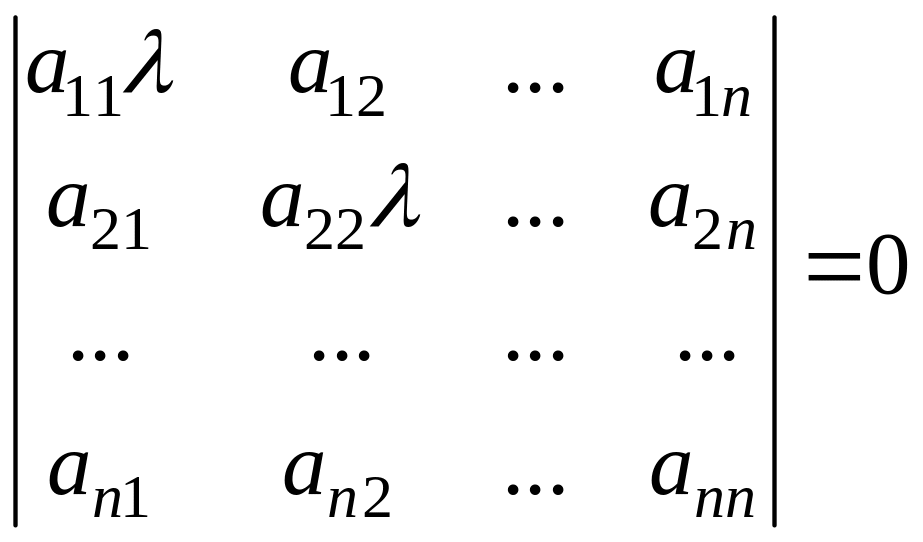
по модулю меньше единицы.
function 9kobi
B=[142; 26; 23; 49];
A=[-83 27 -13 -11; 5 -68 13 24; 9 54 127 36;13 27 34 156];
% количество итераций
NumIter=100;
%=========================================
x1=0; x2=0; x3=0; x4=0;
for i=1:NumIter
x1(i+1)=-(A(1,2).*x2(i)+A(1,3).*x3(i)+A(1,4).*x4(i)-B(1))/A(1,1);
x2(i+1)=-(A(2,1).*x1(i)+A(2,3).*x3(i)+A(2,4).*x4(i)-B(2))/A(2,2);
x3(i+1)=-(A(3,1)*x1(i)+A(3,2).*x2(i)+A(3,4).*x4(i)-B(3))/A(3,3);
x4(i+1)=-(A(4,1)*x1(i)+A(4,2).*x2(i)+A(4,3).*x3(i)-B(4))/A(4,4);
if rem(x1(i+1),x1(i))==0
N=i;
disp(['число итераций=' num2str(N)])
disp([' X1= ', ' X2= ', ' X3= ', ' X4= '])
disp([x1(N) x2(N) x3(N) x4(N)])
break
else disp('система не сходится')
end;
end;
система не сходится