Министерство образования и науки РФ
Калужский филиал МГТУ им. Н.Э. Баумана
Домашнее задание № 1 Методы решения систем линейных алгебраических уравнений
Группа: САУ-51
Студент: Тюваев И.Н.
Принял: Мышляев Ю.И.
Калуга 2011
Цель работы: изучение точных методов (Гаусса, LU-разложения, квадратных корней, вращений) и итерационных методов (простых итераций, Якоби, Зейделя) решения систем линейных алгебраических уравнений.
1.1. Задание
1. Определить число обусловленности матрицы системы линейных алгебраических уравнений (СЛАУ).
2. Решить СЛАУ точными методами:
2.1. Методом Гаусса с выбором главного элемента,
2.3. Методом LU – разложения,
2.4. Методом вращений.
3. Решить СЛАУ итерационными методами:
3.1. Методом простых итераций (МПИ)
3.2. Методом Якоби или Зейделя.
4. Провести сравнительный анализ методов решений СЛАУ с точки зрения жесткости системы, точности, условий сходимости методов, вычислительной сложности.
1.2. Пример выполнения задания Постановка задачи
Решить систему линейных алгебраических уравнений вида
Дана система линейных алгебраических уравнений:
Ax=b, где
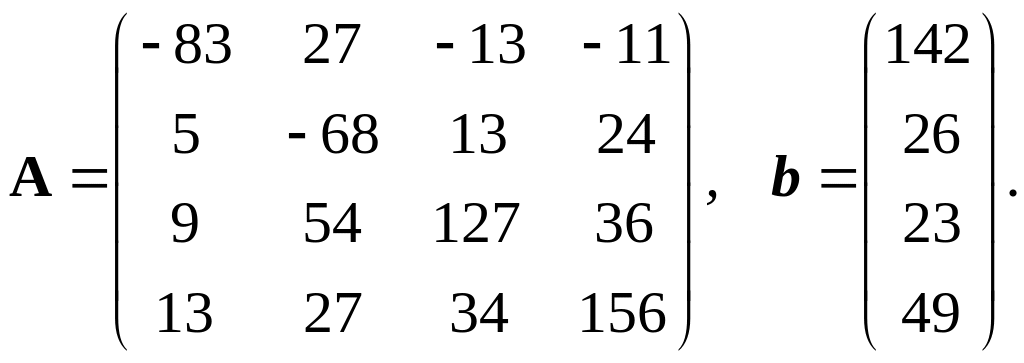
Метод Гаусса с выбором главного элемента.
Суть
метода Гаусса заключается в последовательном
исключении элементов. Для этого поэтапно
приводим систему (1) к треугольному виду,
исключая последовательно
из второго, третьего, … , n-го уравнений,
затем
из третьего, четвёртого, … , n-го уравнений
преобразованной системы и т.д.
Практическая часть (листинг программы MatLab):
function gauss
clc
b=[142; 26; 23; 49];
A=[-83 27 -13 -11; 5 -68 13 24; 9 54 127 36;13 27 34 156];
max=0;
x=[0;0;0;0];
x1=[0;0;0;0];
ind=[1;2;3;4];
t=0;
a1=0;
b1=0;
n=4;
ind1=0;
k=1;
A,b
for k=1:n-1
max=abs(A(k,k));
for n1=k:4
for s=k:4
if(abs(A(n1,s))>max),
max=abs(A(n1,s));
mi=n1;
mj=s;
end;
end;
end;
b1=b(mi);
b(mi)=b(k);
b(k)=b1;
for n2=k:4
a1=A(mi,n2);
A(mi,n2)=A(k,n2);
A(k,n2)=a1;
end;
for n3=1:4
a1=A(n3,mj);
A(n3,mj)=A(n3,k);
A(n3,k)=a1;
end;
ind1=ind(mj);
ind(mj)=ind(k);
ind(k)=ind1;
for i=(k+1):4
t=A(i,k)./A(k,k);
b(i)=b(i)-b(k).*t;
for j=k:4
A(i,j)=A(i,j)-A(k,j).*t;
end;
end ;
end;
x1(4,1)=b(4,1)/A(4,4);
x1(3,1)=(b(3,1)-A(3,4)*x1(4,1))/A(3,3);
x1(2,1)=(b(2,1)-A(2,3)*x1(3,1)-A(2,4)*x1(4,1))/A(2,2);
x1(1,1)=(b(1,1)-A(1,2)*x1(2,1)-A(1,3)*x1(3,1)-A(1,4)*x1(4,1))/A(1,1);
for i=1:4
for j=1:4
if (ind(i)==j)
x(j,1)=x1(i,1);
end;
end;
end ;
x1
x
Результат работы алгоритма:
A =
-83 27 -13 -11
5 -68 13 24
9 54 127 36
13 27 34 156
b =
142
26
23
49
x1 =
0.4574
0.3157
-1.9190
-0.3017
x =
-1.9190
-0.3017
0.3157
0.4574
LU-разложение.
Теорема: если главные миноры квадратной матрицы А отличны от нуля, то существуют такие нижняя L и верхняя U треугольные матрицы, что A=LU. Если элементы диагонали одной из матриц L или U фиксированы (ненулевые), то такое разложение единственно.
Если
матрица А исходной системы разложена
в произведение треугольных матриц L и
U, то вместо Ax=b можно записать эквивалентное
уравнение LUx=b. Введя вектор вспомогательных
переменных
,
последнее можно переписать в виде
системы
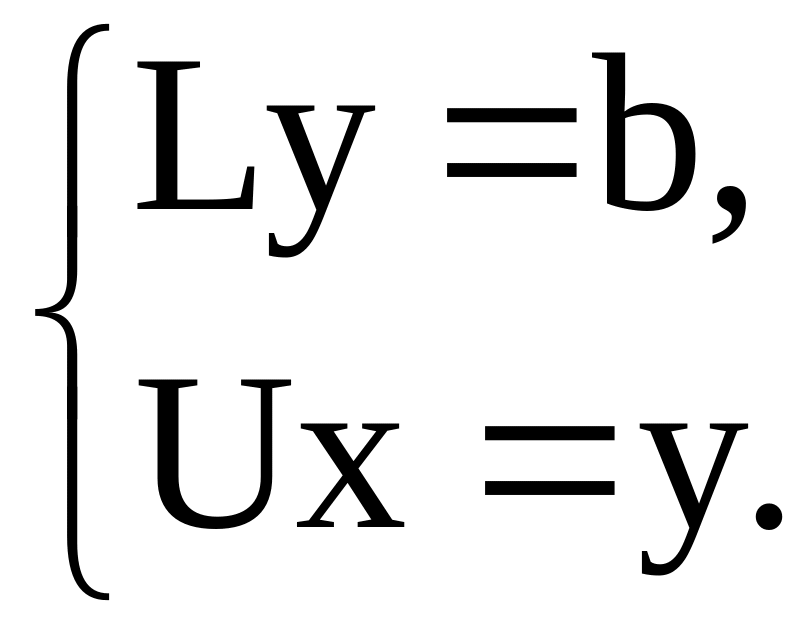
Таким образом, решение данной системы с квадратной матрицей коэффициентов свелось к последовательному решению двух систем с треугольными матрицами коэффициентов.
Практическая часть (листинг программы MatLab)
function LU;
B=[142; 26; 23; 49];
B
A=[-83 27 -13 -11; 5 -68 13 24; 9 54 127 36;13 27 34 156];
A
X=zeros(4,1);
Y=zeros(4,1);
U=zeros(4,4);
L=zeros(4,4);
for i=1:4,
for j=i:4,
if i==j,
L(i,j)=1;
end
end
end
U(1,1)=A(1,1);
U(1,2)=A(1,2);
U(1,3)=A(1,3);
U(1,4)=A(1,4);
L(2,1)=A(2,1)/U(1,1);
L(3,1)=A(3,1)/U(1,1);
L(4,1)=A(4,1)/U(1,1);
U(2,2)=A(2,2)-L(2,1)*U(1,2);
U(2,3)=A(2,3)-L(2,1)*U(1,3);
U(2,4)=A(2,4)-L(2,1)*U(1,4);
L(3,2)=(A(3,2)-L(3,1)*U(1,2))/U(2,2);
U(3,3)=A(3,3)-L(3,1)*U(1,3)-L(3,2)*U(2,3);
U(3,4)=A(3,4)-L(3,1)*U(1,4)-L(3,2)*U(2,4);
L(4,2)=(A(4,2)-L(4,1)*U(1,2))/U(2,2);
L(4,3)=(A(4,3)-L(4,1)*U(1,3)-L(4,2)*U(2,3))/U(3,3);
U(4,4)=A(4,4)-L(4,1)*U(1,4)-L(4,2)*U(2,4)-L(4,3)*U(3,4);
L
U
Y=L\B;X=U\Y;
X1=X(1);X2=X(2);X3=X(3);X4=X(4);
X
Результат работы алгоритма:
B =
142
26
23
49
A =
-83 27 -13 -11
5 -68 13 24
9 54 127 36
13 27 34 156
L =
1.0000 0 0 0
-0.0602 1.0000 0 0
-0.1084 -0.8577 1.0000 0
-0.1566 -0.4705 0.2772 1.0000
U =
-83.0000 27.0000 -13.0000 -11.0000
0 -66.3735 12.2169 23.3373
0 0 136.0686 54.8234
0 0 0 150.0629
X =
-1.9190
-0.3017
0.3157
0.4574