
Кореляційна матриця економічних показників
-
у
х1
х2
у
1
х1
0,6903
1
х2
0,4077
0,8192
1
Після аналізу кореляційної матриці можна зробити висновок, що коефіцієнти х1 і х2 мають велике значення коефіцієнту кореляції і це може свідчити про наявність лінійної залежності між ними. На основі даного висновку можна говорити про наявність мультиколінеарності в даній моделі.
2. Визначимо ступінь колінеарності. У разі відсутності мультиколінеарності у моделі множинний коефіцієнт детермінації R2yx1x2 буде приблизно дорівнювати сумі часткових коефіцієнтів детермінації R2yx1, R2yx2, R2x1x2. Якщо мультиколенеарність присутня, тоді це рівняння виконуватись не буде і у якості виміру мультиколінеарності можна використати змінну М1:
М1 = R2yx1x2 – ( R2yx1 + R2yx2 +R2x1x2 ).
Чим більше змінна М1 наближатиметься до нуля, тим менша мультиколінеарність.
Відповідно, до нашого приклада: М1 =0,552221 - 0,476488 - 0,166228 - 0,67118.
3. Перевіримо інтенсивність мультиколінеарності за формулою:
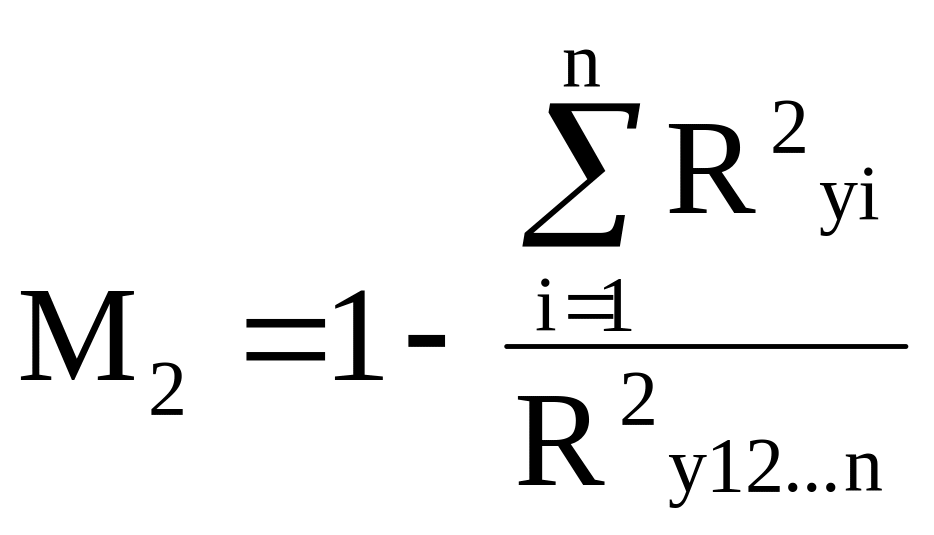
Відповідно до нашого приклада отримаємо: 0,476488 + 0,166228 + 0,67118 = 1,31; 1,31/0,55=2,38. М2 = 1 - 2,38 = 1,38. Даний коефіцієнт значно більший нуля, тому можна говорити про високу інтенсивність мультиколінеарності.
4. Одним із методів усунення мультиколінеарності є метод головних компонент. Застосуємо його для нашого прикладу.
4.1. Розрахуємо нормалізовані змінні х1* і х2* (табл.4).
Таблиця 4
Розрахунок нормалізованих змінних
-
y
x1
x2
Х1*
х2*
1
4,2
6,9
6
0,377102
0,560645
2
1,5
2,9
5,4
-0,97188
0,259811
3
2,8
3,5
3,1
-0,76953
-0,89339
4
5,6
9,1
7,2
1,119042
1,162313
5
2,5
5,2
4,6
-0,19622
-0,1413
6
3,9
6,5
3,9
0,242204
-0,49227
7
3,8
2,9
3,8
-0,97188
-0,54241
8
4,6
1,4
2,6
-1,47775
-1,14408
9
4,9
8,8
6,8
1,017869
0,961757
10
7,2
11,5
8,5
1,928432
1,81412
11
5,3
4,9
1,8
-0,29739
-1,54519
4.2. Побудуємо кореляційну матрицю нормалізованих змінних х1* і х2*. Зробимо це за допомогою табличного процесору Excel. Виберемо пункт меню "Сервіс", підпункт "Аналіз даних". У вікні, що з'явилось виберемо опцію "Кореляція" і натиснемо на кнопку "ОК". У полі "Входной интервал" запишемо область даних, де розміщуються значення нормалізованих змінних х1* і х2* (наприклад, C4:D15) і натиснемо кнопку "ОК". На новому листі отримаємо кореляційну матрицю у вигляді:
-
Столбец 1
Столбец 2
або
Х1*
Х2*
Столбец 1
1
Х1*
1
Столбец 2
0,819116
1
Х2*
0,819116
1
4.3. Знайдемо власні значення . Із кореляційної матриці отримаємо:
-
1-
0,819116
= (1-)*(1-) – 0,819116*0,819116 = 0
0,819116
1-
(1-)2 = 0,8191162
1- = 0,819116
1 = 1 – 0,819116 = 0,180884
2 = 1 + 0,819116 = 1,819116
4.4. Обчислимо власні вектори аk:
для 1 = 0,180884 матриця буде мати вигляд
![]()
Припустимо а11 = 1, тоді а12 = -1. Нормалізуємо вектор а1.
Елементи нормалізованого вектору а1 отримаємо із вимоги нормалізації:
![]()
Тоді власний вектор а1 буде мати вигляд:
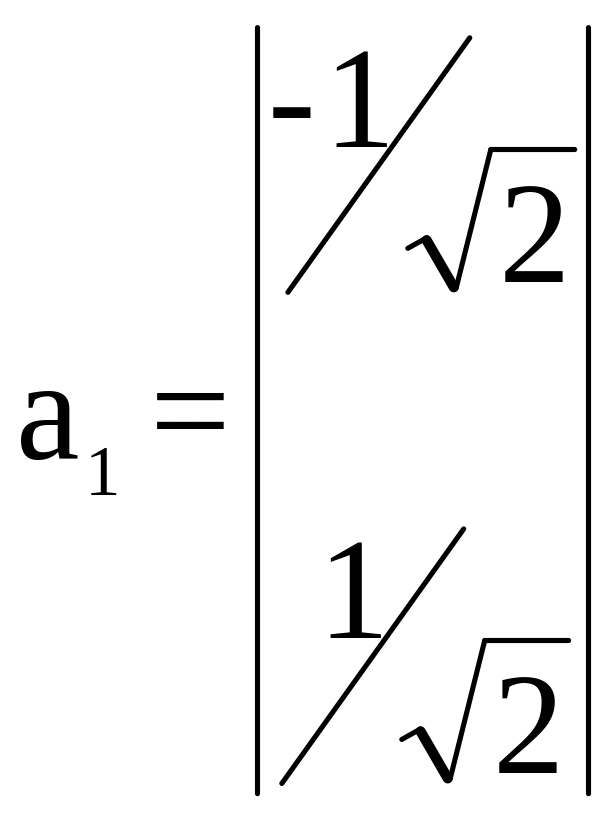 .
.
Для 2 = 1,819116 матриця буде мати вигляд:
![]() .
.
Припустимо а21 = 1, тоді а22 = 1. Нормалізуємо вектор а2.
Елементи нормалізованого вектору а2 отримаємо із вимоги нормалізації:
![]()
Тоді власний вектор а1 буде мати вигляд:
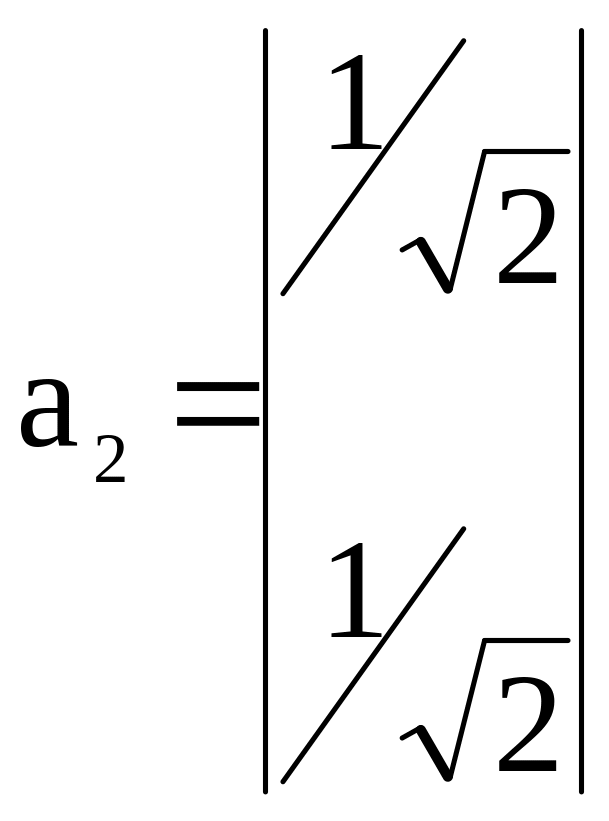 .
.
Отримаємо матрицю власних векторів Аk :
 .
.
Розрахуємо елементи матриці Z. У загальному вигляді: Z1 = X a1 і Z2 = X a2.
Наприклад, елементи матриці zі1 = xi1a11 + xi2a12, де і = 1..n (n – кількість спостережень).
Розрахуємо рівняння регресії, що відповідає залежності:
![]() .
.
Коефіцієнти b0, b1, b2 отримуються по аналогії з розрахунками коефіцієнтів багатофакторної регресії у лабораторній роботі №3.
Отримаємо бета-коефіцієнти (0, 1, 2) по значенням b0, b1, b2 .
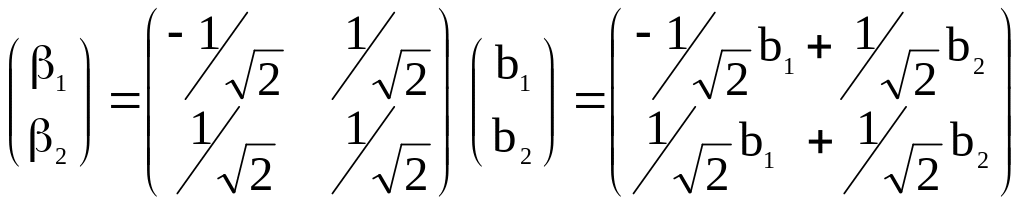 .
.
Остаточне рівняння з відсутньою мультиколінеарністю матиме вигляд:
![]() .
.
Всі розрахунки по усуненню мультиколінеарності наведені в табл. 5.
Таблиця 5
Метод головних компонентів
|
y |
x1 |
x2 |
х1-хср |
х2-хср |
(х1-хср)2 |
(х2-хср)2 |
норм(х1) |
норм(х2) |
z1 |
z2 |
у регр |
у-урегр |
1 |
4,2 |
6,9 |
6 |
1,12 |
1,12 |
1,25 |
1,25 |
0,38 |
0,56 |
-0,64 |
9,12 |
4,42 |
-0,22 |
2 |
1,5 |
2,9 |
5,4 |
-2,88 |
0,52 |
8,30 |
0,27 |
-0,97 |
0,26 |
1,77 |
5,87 |
2,41 |
-0,91 |
3 |
2,8 |
3,5 |
3,1 |
-2,28 |
-1,78 |
5,21 |
3,17 |
-0,77 |
-0,89 |
-0,28 |
4,67 |
3,60 |
-0,80 |
4 |
5,6 |
9,1 |
7,2 |
3,32 |
2,32 |
11,01 |
5,37 |
1,12 |
1,16 |
-1,34 |
11,53 |
5,20 |
0,40 |
5 |
2,5 |
5,2 |
4,6 |
-0,58 |
-0,28 |
0,34 |
0,08 |
-0,20 |
-0,14 |
-0,42 |
6,93 |
3,99 |
-1,49 |
6 |
3,9 |
6,5 |
3,9 |
0,72 |
-0,98 |
0,52 |
0,96 |
0,24 |
-0,49 |
-1,84 |
7,35 |
4,97 |
-1,07 |
7 |
3,8 |
2,9 |
3,8 |
-2,88 |
-1,08 |
8,30 |
1,17 |
-0,97 |
-0,54 |
0,64 |
4,74 |
3,01 |
0,79 |
8 |
4,6 |
1,4 |
2,6 |
-4,38 |
-2,28 |
19,20 |
5,21 |
-1,48 |
-1,14 |
0,85 |
2,83 |
2,62 |
1,98 |
9 |
4,9 |
8,8 |
6,8 |
3,02 |
1,92 |
9,11 |
3,68 |
1,02 |
0,96 |
-1,41 |
11,03 |
5,18 |
-0,28 |
10 |
7,2 |
11,5 |
8,5 |
5,72 |
3,62 |
32,70 |
13,09 |
1,93 |
1,81 |
-2,12 |
14,14 |
6,05 |
1,15 |
11 |
5,3 |
4,9 |
1,8 |
-0,88 |
-3,08 |
0,78 |
9,50 |
-0,30 |
-1,55 |
-2,19 |
4,74 |
4,86 |
0,44 |
Значення і власних векторів ак дивіться по тексту лабораторної роботи.
